кр3 / кр3вар2
.docВариант2
1. Дана матрица распределения вероятностей системы (X,Y)
-
X
Y
1
2
3
1
0,1700
0,1300
0,2500
2
0,1000
0,3000
0,0500
Найти: а.) ряды распределений X
и Y ; б.) (561.Д7)
;
в.) (560.Д7)
;
г.) (821.Д5)
;
д.) (ДТ1.Д5)
;
е.) (731.Д4) cov(X,Y);
ж.) (041.Д7)
,
округлить до 0,1; з.) ряд распределения
Y, если X
=3; и.) (3П1.Д7) М[Y/X=3],
округлить до 0,01.
Решение:
а.) Суммируя по столбцам, а затем по строкам элементы матрицы распределения, найдём искомые ряды распределения:
Ряд распределения Х:
-
X
1
2
3
p
0,2700
0,4300
0,3000
Ряд распределения Y:
-
Y
1
2
p
0,5500
0,4500
б.)
находим
по формуле:
используя ряд распределения X:
=1*0,27
00+2*0,4300+3*0,3000=2,0300.
в)
находим по формуле:
,
используя ряд распределения Y:
=1*0,5500+2*0,4500=1,4500.
г.)
Найдём
по формуле:
:
=
д.)
Найдём
по формуле:
:
=
е.)
Для числовой характеристики степени
зависимости величин X и
Y используем величину
,
называемую ковариацией:
;
;
В нашем случае:
Cov(X,Y)=2,88-2,03·1,45=-0,064.
ж) Коэффициент корреляции :
=
X и Y являются
коррелированными.
з.) Ряд распределения Y при X = 3 находится, используя:
Следовательно:
|
Y / X =3 |
1 |
2 |
|
p |
0,83 |
0,17 |
и.)
найдём, используя ряд распределения У
при Х =3:
=
1∙0,83 + 2·0,17 =1,17.
ОТВЕТ:
=2,0300;
=1,4500;
=
0,5691;
=0,248;
cov(X,Y)=
- 0,064;
=
- 0,2;
=1,17.
-
Дана плотность распределения вероятностей системы:
Найти: а.) (221) константу С ; б.)
,
;
в.) (971)
;
г.) (472)
;
д.) (131)
;
е.) (1Т1)
;
ж.) (П32), cov(X,Y)
; з.) (ПР1)
;
и.) (6Р2)
;
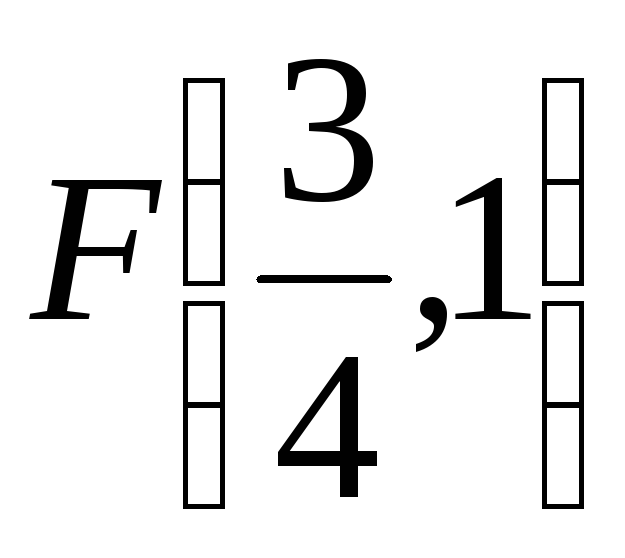к.) (7Р3) М[Y/X=
].
Решение:
а.) Константу С найдём из условия нормировки:
,
где D – область, ограниченная
сторонами треугольника ОАВ.
Так как прямая (ОВ):
,
следовательно:
б.)
Плотность распределения случайной
величины Х находим по формуле:
При фиксированном x
из промежутка (0<x<1)
переменная у меняется
:
.
Плотность распределения случайной
величины y находим по
формуле :
При фиксированном у из промежутка
(0<y<2) переменная х
меняется
:
,
.
=
=
в.) Математическое ожидание случайной величины х:
.
г.) Математическое ожидание случайной величины y:
.
д.)
Найдем дисперсию
случайной величины х:
;
;
;
е.)
Найдем дисперсию
случайной величины у:
;
ж.) Находим ковариацию:
;
=0,5-0,667∙0,667=0,111;
з.) Коэффициент корреляции:
=
и.)
;
;
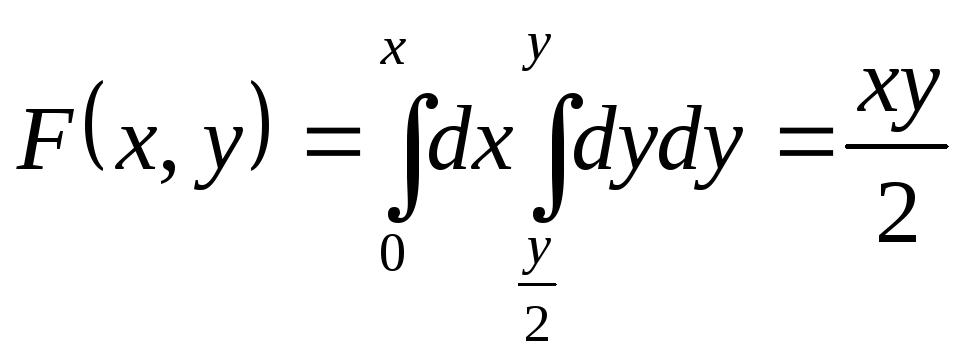к.) Условное математическое ожидание:
=
; 
,
при
ОТВЕТ: а.) С=1 ; б.)
=2х,
=
;
в.)
=0,667;
г.)
=0,667;
д.)
=0,056;
е.)
=0,222;
ж.)cov(X,Y)=
0,111; з.)
=0,99;
и.)
=0,375
; к.) М[Y/X=
]=
.
3(552.Д7). Среднее квадратичное отклонение
нормальной случайной величины Х
равно 10 единицам. Для выборки объёма
100 построить доверительный интервал
для оценки математического ожидания
с надёжностью
=0,95,
если выборочное математическое ожидание
равно шести единицам. В ответ ввести
координату правого конца интервала.
Решение:
,
n=100,
,
В нашем случае
.
По
таблице для функции Лапласа находим
t=1,96.
Следовательно,
.
Тогда из неравенства
следует,
что с вероятностью 0,95 справедливо
неравенство
.
ОТВЕТ: координата правого конца интервала 7,96.
1. Дана матрица распределения вероятностей системы (X, Y).
|
|
X |
||
|
Y |
1 |
2 |
5 |
|
2 |
0.1000 |
0.2500 |
0.3000 |
|
4 |
0.1500 |
0.1000 |
0.1000 |
Вариант10
Найти: а). ряды распределений X и Y; б). mx ; в). my; г). D ; е). cov(X, Y); ж). rxy; з). Ряд распределений Y, если X=2; и). M[X/Y=2].
Решение:
Ряд распределения X находим, суммируя вероятности в столбцах, а ряд распределения Y - в строках.
|
|
X |
1 |
2 |
5 |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
P |
0,2500 |
0,3500 |
0,4000 |
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|||||||
|
Y |
2 |
4 |
|
P |
0.6500 |
0.3500 |
Б).
В).
Г).
Д).
Е).
Ж).
З) Находим условные вероятности
Ряд распределения y при x=2
|
X |
2 |
4 |
|
p |
5/7 |
2/7 |
и)
-
Дана плотность распределения вероятностей системы (x,y)
Найти: а) константу С; б)1(x), 2(y); в) mx ; г) my ; д) Dx ; е) Dy; ж) cov (x,y); з) rxy; и). F(-1, 5); к). M[x/y=1];
А
).
Y
B - 4
Y=-4/3X
X=-3/4Y
A
-3 0 X
Б
).
Таким образом,
в
)
г
)
д
)
е
)
ж
)
з)
и) F(-1,5)=?
к) Для начала найдём условную плотность
распределения
Теперь
находим условное математическое
ожидание:
3. Найти доверительный интервал для оценки математического ожидания а нормального распределения с надёжностью = 0,95, зная, что m = 60, n=49, k=7. В ответ ввести координату левого конца построенного доверительного интервала.
Решение:
В данном случае
По таблице для функции Лапласа находим
t=1,96. Следовательно,
Итак строим доверительный интервал:
60 - 1,96 < a < 60 + 1,96
58,04 < a < 61,96
Координата левого конца доверительного интервала равна 58,04.
Вариант2
-
Дана матрица распределения вероятностей системы (Х, Y)
-
X
Y
1
2
3
1
0.1700
0.1300
0.2500
2
0.1000
0.3000
0.0500
Найти:
а) ряды распределений Х и Y;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
,
округлить до 0.1; з) ряд распределения Y,
если Х =3; и)
,
округлить до 0.01.
решение:
a)
-
1
2
3
1
0.1700
0.1300
0.2500
0.55
2
0.1000
0.3000
0.0500
0.45
0.27
0.43
0.30
1
-
1
2
3
0.27
0.43
0.30
-
1
2
0.55
0.45
б)
в)
г)
д)
е)
ж)
з)
-
1
2
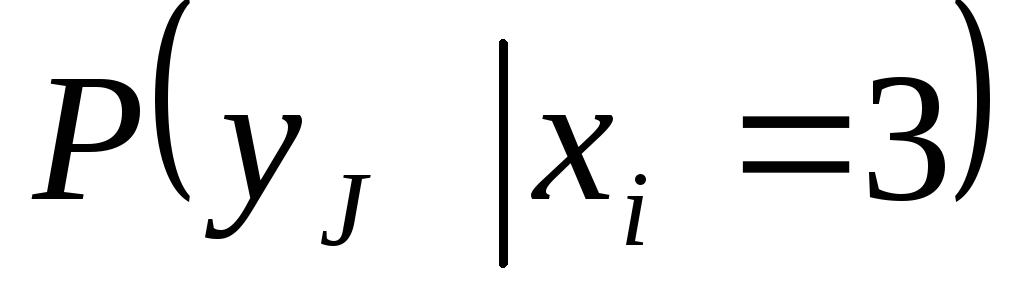
и)
-
Дана плотность распределения вероятностей системы
Найти:
а) константу С; б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
;
и)
;
к)
.
решение:
а)
б)
Вариант4
-
Дана матрица распределения вероятностей системы (х, у):
|
|
х |
||
|
у |
1 |
2 |
3 |
|
1 |
0,1 |
0,19 |
0.2 |
|
2 |
0,16 |
0,2 |
0,15 |
Найти: а) ряды распределений
Х и У ; б)
;
в)
;
г)
;
д)
;
е)
ж) r
;з)
ряд распределения Х, если У=1; и)
