Конспект лекций Глазова / 3.8. Некот непрер. распр

3.8. Некоторые непрерывные распределения.

• Равномерное (прямоугольное) распределение. Это простейшее непрерывное распределение с плотностью вероятности, постоянной на конечном интервале и равной нулю вне этого интервала. Записав плотность в виде

определим А из условия нормировки: площадь под кривой плотности (b-a)A=1, откуда A=1/(b-a). Функция распределения

т. е.

линейна в области, где f(x) отлична от нуля (см. рис. 3.8.1).

Рисунок 3.8.1.

Равномерное распределение.

Начальный момент порядка k

,

в частности,

,

т. е. с. к. о. в раз меньше полуширины (b-a)/2 распределения.

Центральные моменты нечетного порядка равны нулю вследствие симметрии распределения, центральные моменты четного порядка

,

в частности,

,

откуда коэффициенты асимметрии и эксцесса

k_as=k_ex=

Характеристическая функция

.

Для четного равномерного распределения, получаемого при a=-g, b=g, где g>0,

,

как и следовало ожидать, четна.

Равномерное распределение часто встречается на практике, например:

а) ошибка округления случайного числа до целых имеет четное равномерное распределение на (-0.5, 0.5);

б) время ожидания поезда метро, следующего строго через 2 минуты, при случайном выходе на перрон - СВ, имеющая равномерное на (0, 2) распределение.

Кроме того, часто равномерное распределение принимается как приближенное в тех случаях, когда известны минимальное и максимальное значения непрерывной СВ, но не известна плотность вероятности.

• Треугольное распределение (распределение Симпсона). Это четное распределение с плотностью вероятности (см. рис. 3.8.2)

где b>0. На самом деле это класс распределений с одним параметром b.

Рисунок 3.8.2.

Треугольное распределение (Симпсона).

Упражнение 3.8.1. Из геометрических соображений проверить нормировку распределения и найти m, k_as , x_mod , x_med .

Упражнение 3.8.2. Убедиться, что функция распределения имеет вид

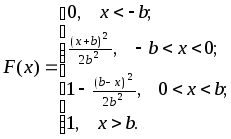
Характеристическая функция имеет вид (без вывода)

,

и, как и следовало ожидать, действительна вследствие симметрии распределения.

Это распределение используется, в частности, в теории ошибок и в цифровой связи, т. к. его имеет СВ, равная сумме двух независимых СВ, распределенных равномерно. Такая ситуация возникает, например, при округлении концевых значений интервала времени.

• Экспоненциальное распределение. Это распределение случайной величины, принимающей неотрицательные значения, с плотностью вероятности (см. рис. 3.8.3)

, , b>0.

На самом деле это класс распределений с одним параметром .

Убедимся, что условие нормировки выполнено:

.

Рисунок 3.8.3.

Плотность вероятности и функция распределения экспоненциального распределения с параметром b=2.

Функция распределения (см. рис. 3.8.3)

Характеристическая функция

.

Из нее находим начальные моменты:

,

откуда

.

Таким образом, смысл параметра - величина, обратная математическому ожиданию. Заметим, что и относительное с. к. о. не зависит от параметра :

.

Экспоненциальное распределение возникает в различных приложениях теории вероятностей, в особенности в теории надежности и теории массового обслуживания. Наиболее важная математическая причина этого - тот факт, что «пустой» интервал в однородном пуассоновском потоке имеет экспоненциальное распределение. Выведем это свойство. Вероятность того, что на интервал длиной однородного пуассоновского потока с плотностью потока b не попадет ни одной точки, дается формулой (2.14.5):

.

С другой стороны, это вероятность того, что длина X «пустого» интервала будет не меньше заданной , т. е.

, >0,

откуда F(x)=1-e^-bx, x>0, и, дифференцируя это равенство, получаем

f(x)=be^-bx , x>0,

т. е. «пустой» интервал имеет экспоненциальное распределение.

• Распределение арксинуса. Это распределение непрерывной СВ, принимающей значения на конечном интервале (-a, a), с плотностью вероятности (см. рис. 3.8.4)

Рисунок 3.8.4.

Плотность вероятности распределения арксинуса.

Упражнение 3.8.3. Убедиться в том, что функция распределения

построить ее и объяснить название распределения.

Это распределение имеет поучительные математические свойства.

а) Плотность вероятности f(x) не ограничена при приближении к точкам а-, а , и имеет в этих точках бесконечный разрыв (эти возможности оговорены в п. 3.3 и не нарушают обязательных требований к f(x)).

б) У этого распределения нет моды (т. к. f(x) не имеет локальных максимумов), но есть антимода x_antmod=0 (эта возможность также оговорена в п. 3.3).

в) Несмотря на неограниченность f(x), интеграл от нее по всей оси сходится и равен 1 (что входит в число обязательных требований), более того, все моменты распределения существуют (что не входит в число обязательных требований). Причина сходимости соответствующих несобственных интегралов - достаточно медленное возрастание f(x) при и .

г) Несмотря на несколько необычные свойства f(x), функция распределения F(x) имеет простой вид и, как и должно быть для непрерывной СВ, она всюду непрерывна.

Не следует думать, что это распределение специально придумано для демонстрации необычных математических свойств; наоборот, оно встречается в практических приложениях, например, такое распределение имеет мгновенное значение важного для статистической радиотехники случайного процесса, называемого «синусоидой со случайной фазой».

Характеристическая функция этого распределения

не выражается конечной комбинацией элементарных функций (т. е. выражается только через специальные функции). Моменты легко найти по определению, беря соответствующие интегралы по частям, но и без вычислений, в силу симметрии распределения, ясно, что m= (и вообще для нечетных центральных моментов). Вычислив D=a²/2, имеем k_as=0.

• Распределение Коши. Так называется распределение непрерывной СВ с плотностью

f(x)=A/(1+x²), , A>0.

Определив А из условия нормировки,

запишем плотность вероятности в виде

f(x)=.

(3.8.1)

Это распределение встречается в физике, геофизике, математической статистике, статистической радиотехнике и других областях. Замечательным свойством этого распределения является то, что все его моменты в обычном смысле (т. е. как интегралы Римана) не существуют. Это означает, что интегралы для моментов

расходятся в обычном смысле при всех k=1, 2, ..., в том числе и математическое ожидание (правило, что для симметричного распределения m и нечетные центральные моменты равны нулю, справедливо только при существовании моментов). Если взять т. н. главное значение интеграла (или в смысле Коши), в данном случае вычисляемое как

,

то при нечетном k получим 0, т. е. математическое ожидание и все нечетные центральные моменты в смысле главного значения равны нулю (в указанном смысле - это следствие симметрии распределения). При четном же k моменты (и в том числе - дисперсия) не существуют уже ни в каком смысле и для характеризации эффективного разброса значений надо применять нетрадиционные меры (см. п. 3.5). . Ясно также, что коэффициенты асимметрии и эксцесса не определены. Тот же результат получится, если найти характеристическую функцию (вывод не приводим)

,

и попытаться искать моменты через ее производные в нуле, т. к. последние не существуют.

• Распределение Лапласа (двустороннее экспоненциальное распределение). Это распределение непрерывной СВ, принимающей значения на всей оси, с плотностью вероятности (см. рис. 3.8.5)

, a>0.

Рисунок 3.8.5.

Распределение Лапласа (двустороннее экспоненциальное).

На самом деле это класс распределений с одним параметром а .

Упражнение 3.8.4. Проверить выполнение условия нормировки и убедиться, что функция распределения

Благодаря быстрому убыванию плотности на бесконечностях, все моменты этого распределения существуют, при этом математическое ожидание m и нечетные центральные моменты равны нулю в силу четности распределения. По этой же причине начальные моменты равны соответствующим центральным. Найдя также

,

,

имеем

,

т. е. это распределение имеет большой положительный эксцесс.

Упражнение 3.8.5. Проверить, что характеристическая функция

.

Распределение Лапласа часто используется в теории надежности.

• Нормальное (гауссово) распределение. Это распределение непрерывной СВ (она также называется нормальной) , принимающей значения на всей оси, с плотностью вероятности

f(x)=Aexp[-Q(x)],

(3.8.2)

где A>0 - коэффициент нормировки, Q(x) - квадратичная функция, принимающая на оси неотрицательные значения. Выделив из Q(x) полный квадрат и записав ее в виде Q(x)=B(x-a)² +C, где B>0, С 0, подставим в (3.8.2):

f(x)=Eexp[-B(x-a)2]

(3.8.3)

где E=Aexp(-C)>0 - новый коэффициент нормировки. Из условия нормировки

,

сделав замену переменных и учитывая интеграл Пуассона

,

находим . Из симметрии плотности (3.8.3) относительно т. а следует, что математическое ожидание

m=a.

(3.8.4)

Как выяснится ниже,

B=1/2.

(3.8.5)

Выражая из (3.8.4), (3.8.5) a, B, E через m, и подставляя в (3.8.3), получаем

f(x)=.

(3.8.6)

Именно в такой форме принято записывать плотность вероятности нормального распределения. Особенность этой формы записи в том, что параметры распределения (их, как видим, два) уже выражены через математическое ожидание m и с. к. о. . Проведенные выше выкладки полезны в тех случаях, когда дана f(x), еще не приведенная к виду (3.8.6). Пусть, например, дано:

f(x)=0.13298exp[-0.05556(x+2)²].

Это выражение имеет форму (3.8.3) при B=0.05556>0, E=0.13298>0, следовательно, это плотность вероятности нормального распределения. Из (3.8.4), (3.8.5) находим m=-2, =3 и записываем f(x) в форме (3.8.6):

.

(3.8.7)

Для краткости записи придумано обозначение

f(x)=N(m, ),

в котором указывается факт нормального распределения (буква N) и значения m, . Например, плотность (3.8.7) запишется как N(-2, 3).

Обсудим свойства плотности (3.8.6). Графики, соответствующие различным m, , показаны на рис. 3.8.6.

Рисунок 3.8.6.

Семейство плотностей вероятности нормального распределения

при различных значениях параметров .

Кривая плотности имеет характерный гладкий колоколообразный вид, с единственным максимумом f_max=1/ в т. m (где показатель экспоненты равен нулю) и точками перегиба . Плотность убывает на бесконечности очень быстро: быстрее x^-n с любым конечным n>0, поэтому существуют моменты любого конечного порядка. Кривая плотности симметрична относительно т. m, поэтому m=x_mod=x_med и все центральные моменты нечетного порядка равны нулю. С увеличением m кривая плотности сдвигается на столько же вправо, с уменьшением m - влево, с увеличением кривая становится шире и ниже, с уменьшением - уже и выше (это соответствует смыслу как меры разброса значений СВ при соблюдении условия нормировки).

Функция распределения

не выражается конечной комбинацией элементарных функций, поэтому, сделав замену переменных , и записав

,

сравним ее со специальной функцией

,

(3.8.8)

называемой интегралом вероятности. Очевидно,

.

(3.8.9)

Практически значения F(x) рассчитывают по таблицам функции , или на компьютере. Свойства F(x) определяются свойствами функции . Из (3.8.8) следует, что всюду монотонно возрастает (т. к. подынтегральная функция положительна); при ; переходя заменой к интегралу Пуассона, видим, что при , а вследствие симметрии подынтегральной функции Функция бесконечно дифференцируема, в частности,

,

и x=0 - точка перегиба функции .

Обращаясь теперь к свойствам функции распределения F(x), видим, что она всюду непрерывна, бесконечно дифференцируема, монотонно возрастает, , в т. m имеет перегиб. Вероятность попадания нормальной СВ в интервал

P(a<X<b)=F(b)-F(a)=.

(3.8.10)

Найдем характеристическую функцию:

;

сделав замену переменных

,

получим

.

Как видим, интегрирование ведется по прямой, отстоящей на вниз от действительной оси. В теории функций комплексного переменного показывается, что путь интегрирования можно деформировать в области аналитичности подынтегральной функции. Поскольку функция exp(-z²) аналитична в любой конечной области, совместим путь интегрирования с действительной осью, тогда последний интеграл превратится в интеграл Пуассона; в результате

.

(3.8.11)

Моменты нормального распределения проще всего находить не по определению, т. к. это требует многократного интегрирования по частям, и не из характеристической функции, т. к. выражения последовательных производных становятся все более громоздкими, а из рекуррентной формулы для центральных моментов, к выводу которой сейчас приступаем. Имеем

.

Сделав замену переменных , получим

.

(3.8.12)

Интегрируя по частям, найдем

т. к. первый член в фигурных скобках равен нулю. С другой стороны, заменив в (3.8.12) k на k-2, получим

(3.8.13)

Сравнивая (3.8.12) и (3.8.13), получаем искомую рекуррентную формулу:

.

(3.8.14)

Начиная с тождества , получаем, что все нечетные центральные моменты равны нулю, что уже отмечалось и является следствием симметрии распределения. Начиная с тождества , и последовательно подставляя результат в (3.8.14), получаем формулу

, k=2, 4, 6, ...,

(3.8.15)

где (k-1)!! - произведение всех нечетных чисел от 1 до k-1 включительно. По ней очень просто находятся четные центральные моменты, по ним, в свою очередь, можно найти начальные моменты, используя (3.4.8). В частности,

(3.8.16)

Отсюда легко получаем k_as=0, k_ex=0, чего следовало ожидать, т. к. распределение симметрично, а эксцесс отсчитывается от нормального распределения.

Особое значение имеет каноническое (стандартное) нормальное распределение:

f(x)=N(0, 1)=exp(-x2/2),

(3.8.17)

с параметрами m=0, =1. Для любой нормальной СВ X плотность вероятности центрированной и нормированной СВ

X_cn=(X-m_x)/ ,

имеет вид(3.8.17). Все характеристики этого распределения получим из выше найденных, положив m=0, =1:

F(x)=P(a<X<b)= exp(-v²/2), , (k=2, 4, ...).

В частности, отсюда следует полезная статистическая интерпретация функции Интеграл вероятности: это функция распределения центрированной и нормированной СВ.

Нормальное распределение - основное (важнейшее) в теории вероятностей и ее приложениях: в математической статистике, теории случайных процессов, статистической радиотехнике и др. Это объясняется тем, что оно очень часто встречается в практических задачах и имеет ряд замечательных математических свойств. Причины частого применения этого распределения:

1. Многие СВ в физике и технике имеют нормальное распределение. Например, при термодинамическом равновесии проекции скоростей молекул газа на любую ось - нормальные СВ.

2. Многие распределения, не являющиеся нормальными, при определенных условиях стремятся к нормальному. Это относится даже к дискретным распределениям, например, биномиальному, пуассоновскому и некоторым другим (см. п. 7.9).

3. Т. н. центральная предельная теорема устанавливает (см. п. 7.8), что распределение случайной величины, равной сумме n случайных величин (возможно, разных), при определенных широких условиях стремится к нормальному при n. Это свойство имеет фундаментальное значение, т. к. очень часто СВ является суммой многих случайных величин. Это относится, например, к случайным ошибкам измерения, к величине отраженного от цели сигнала в радиолокации и т. д.