Конспект лекций Глазова / 3.4. Моменты

3.4. Моменты случайной величины.

Выше мы познакомились с исчерпывающими характеристиками СВ: функцией распределения и рядом распределения - для дискретной СВ, функцией распределения и плотностью вероятности - для непрерывной СВ. Эти попарно эквивалентные по информационному содержанию характеристики представляют собой функции и полностью описывают СВ с вероятностной точки зрения. Однако, во многих практических ситуациях или невозможно, или нет необходимости характеризовать случайную величину исчерпывающим образом. Зачастую бывает достаточно указать один или несколько числовых параметров, до некоторой степени описывающих основные черты распределения, а иногда нахождение исчерпывающих характеристик является хотя и желательным, но слишком трудным математически, и оперируя числовыми параметрами, мы ограничиваемся хотя и приближенным, но более простым описанием. Указанные числовые параметры называются числовыми характеристиками случайной величины и играют большую роль в применениях теории вероятности к различным областям науки и техники, облегчая решение задач и позволяя представить результаты решения в простой и наглядной форме.

Наиболее часто применяемые числовые характеристики можно условно разбить на два вида: моменты и характеристики положения. Существует несколько видов моментов, из них наиболее часто применяются два вида: начальные и центральные. Другие виды моментов, например, абсолютные моменты, факториальные моменты, мы не рассматриваем. Чтобы избегнуть применения обобщения интеграла - так называемого интеграла Стильтьеса, дадим определения моментов по отдельности для непрерывных и дискретных СВ.

Определения. 1. Начальным моментом k-го порядка дискретной СВ называется величина

, k=0, 1, 2, ...

(3.4.1)

где {x_i} , i=1, 2, ..., N - значения СВ, {p_i} , i=1, 2, ..., N - вероятности этих значений, N - число значений (при бесконечном числе значений следует вместо N писать ).

2. Начальным моментом k-го порядка непрерывной СВ называется величина

, k=0, 1, 2, ...

(3.4.2)

где f(x) - плотность вероятности данной СВ.

3. Центральным моментом k-го порядка дискретной СВ называется величина

, k=0, 1, 2, ...

(3.4.3)

где m= - начальный момент первого порядка (об этой важной величине см. ниже), остальные обозначения в правой части - те же, что и в (3.4.1).

4. Центральным моментом k-го порядка непрерывной СВ называется величина

, k=0, 1, 2, ...

(3.4.4)

В случаях, когда одновременно в рассмотрении находятся несколько СВ, удобно, во избежание недоразумений, указывать принадлежность момента; мы будем это делать, указывая обозначение соответствующей СВ в скобках, например, , и т. д. Не следует путать это обозначение с записью функции, а букву в скобках - с аргументом функции. Суммы и интегралы в правых частях равенств (3.4.1 - 3.4.4) могут сходиться или расходиться в зависимости от значения k и конкретного распределения. В первом случае говорят, что момент не существует или расходится, во втором - что момент существует или сходится. Если у дискретной СВ конечное число конечных значений (N конечно), то все ее моменты конечного порядка k существуют. При бесконечном N, начиная с некоторого k и для бо¢льших порядков, моменты дискретной СВ (одновременно начальные и центральные) могут не существовать. Моменты непрерывной СВ, как видно из определений, выражаются несобственными интегралами, которые могут расходится, начиная с некоторого k и для бо¢льших порядков (одновременно начальные и центральные). Моменты нулевого порядка всегда сходятся.

Рассмотрим более подробно сначала начальные, а затем центральные моменты. С математической точки зрения начальный момент k-го порядка есть «взвешенное среднее» k-ых степеней значений СВ; в случае дискретной СВ весами являются вероятности значений, в случае непрерывной СВ весовой функцией является плотность вероятности. Такого рода операции широко применяются в механике для описания распределения масс (статические моменты, моменты инерции и т. д.); возникающие в связи с этим аналогии рассмотрены ниже.

Для лучшего понимания начальных моментов рассмотрим их отдельно при заданных k. В теории вероятностей наиболее важны моменты низших порядков, т. е. при малых k, поэтому рассмотрение следует вести в порядке возрастания значений k. Начальный момент нулевого порядка равен

=1 , для дискретной СВ;

=1 , для непрерывной СВ,

т.е. для любой СВ он равен одному и тому же значению - единице, и поэтому не несет никакой информации о статистических свойствах СВ.

Начальный момент первого порядка (или первый начальный момент) равен

, для дискретной СВ;

, для непрерывной СВ.

Этот момент - важнейшая числовая характеристика любой СВ, чему есть несколько взаимосвязанных причин. Во-первых, согласно теореме Чебышёва (см. п. 7.4), при неограниченном числе испытаний над СВ среднее арифметическое наблюденных значений стремится (в некотором смысле) к , таким образом, для любой СВ - это характерное число, вокруг которого группируются ее значения на опыте. Во-вторых, для непрерывной СВ численно равен х-овой координате центра тяжести криволинейной трапеции, образуемой кривой f(x) (аналогичное свойство имеет место и для дискретной СВ), поэтому этот момент можно было бы назвать «центром тяжести распределения». В-третьих, этот момент имеет замечательные математические свойства, которые выяснятся в процессе прохождения курса, в частности, поэтому его величина входит в выражения для центральных моментов (см. (3.4.3) и (3.4.4)).

Важность этого момента для теоретических и практических задач теории вероятностей и его замечательные математические свойства привели к тому, что кроме обозначения и названия «первый начальный момент» в литературе используются и другие обозначения и названия, в большей или меньшей мере удобные и отражающие упомянутые свойства. Наиболее часто встречаются названия: математическое ожидание, среднее значение, и обозначения: m, M[X], . Мы будем чаще всего использовать термин «математическое ожидание» и обозначение m; при наличии нескольких СВ будем использовать нижний индекс, указывающий принадлежность математического ожидания, например, m_x , m_y и т. д.

Начальный момент второго порядка (или второй начальный момент) равен

, для дискретной СВ;

, для непрерывной СВ;

иногда он называется средним квадратом случайной величины и обозначается M[].

Начальный момент третьего порядка (или третий начальный момент) равен

, для дискретной СВ;

, для непрерывной СВ

иногда он называется средним кубом случайной величины и обозначается M[X³].

Нет смысла продолжать дальше перечисление начальных моментов. Остановимся на важной интерпретации моментов порядка k>1. Пусть, наряду со СВ X имеется также СВ Y, причем Y=X^k (k=2, 3, ...). Это равенство означает, что случайные величины X и Y связаны детерминировано в том смысле, что когда СВ X принимает значение x, СВ Y принимает значение y=x^k (в дальнейшем такая связь СВ будет рассмотрена более подробно). Тогда, согласно (3.4.1) и (3.4.2)

=m_y , k=2, 3, ...,

т. е. k-ый начальный момент СВ равен математическому ожиданию k-ой степени этой случайной величины. Например, третий начальный момент длины ребра случайного кубика равен математическому ожиданию объема кубика. Возможность понимания моментов как неких математических ожиданий - еще одна грань важности понятия математического ожидания.

Перейдем к рассмотрению центральных моментов. Поскольку, как выяснится несколько ниже, центральные моменты однозначно выражаются через начальные и наоборот, встает вопрос, зачем вообще нужны центральные моменты и почему недостаточно начальных моментов. Рассмотрим СВ X (непрерывную или дискретную) и другую СВ Y, связанную с первой как Y=X+a , где a0 - неслучайное вещественное число. Каждому значению x случайной величины X соответствует значение y=x+a случайной величины Y, следовательно распределение СВ Y будет иметь ту же форму (выраженную многоугольником распределения в дискретном случае или плотностью вероятности - в непрерывном случае), что и распределение СВ X, но сдвинуто по оси абсцисс на величину a . Следовательно, начальные моменты СВ Y будут отличаться от соответствующих моментов СВ X. Например, как нетрудно видеть, m_y=m_x+a (моменты более высокого порядка связаны более сложными соотношениями). Итак, мы установили, что начальные моменты не инвариантны относительно сдвига распределения в целом. Тот же результат получится, если сдвигать не распределение, а начало оси абсцисс по горизонтали на величину -a, т.е. справедлив и эквивалентный вывод: начальные моменты не инвариантны относительно сдвига начала оси абсцисс по горизонтали.

От этого недостатка свободны центральные моменты, предназначенные для описания тех свойств распределений, которые не зависят от их сдвига в целом. Действительно, как видно из (3.4.3) и (3.4.4), при сдвиге распределения в целом на величину a, или, что то же самое, сдвиге начала оси абсцисс на величину -a, все значения x, при тех же вероятностях (в дискретном случае) или той же плотности вероятности (в непрерывном случае), изменятся на величину a, но настолько же изменится величина m, так что значения скобок в правых частях равенств не изменятся. Таким образом, центральные моменты инвариантны относительно сдвига распределения в целом, или, что то же самое, относительно сдвига начала оси абсцисс по горизонтали. Название «центральные» эти моменты получили в те времена, когда первый начальный момент назывался «центром». Полезно заметить, что центральный момент СВ X можно понимать как соответствующий начальный момент СВ X⁰, равной

X0=X-mx .

(3.4.5)

СВ X⁰ называется центрированной (по отношению к СВ X), а приводящая к ней операция, т. е. вычитание из случайной величины ее математического ожидания, называется центрированием. Как мы увидим в дальнейшем, это понятие и эта операция будут полезны на протяжении всего курса. Заметим, что центральный момент порядка k>1 можно рассматривать как математическое ожидание (среднее) k-ой степени центрированной СВ: .

Рассмотрим по отдельности центральные моменты низших порядков. Центральный момент нулевого порядка равен

, для дискретных СВ;

, для непрерывных СВ;

т. е. для любой СВ и не несет никакой информации о статистических свойствах этой СВ.

Центральный момент первого порядка (или первый центральный момент) равен

,

для дискретной СВ;

,

для непрерывной СВ; т. е. для любой СВ и не несет никакой информации о статистических свойствах этой СВ.

Центральный момент второго порядка (или второй центральный момент) равен

, для дискретной СВ;

, для непрерывной СВ.

Как выяснится ниже, этот момент - один из важнейших в теории вероятностей, т. к. используется как характеристика меры разброса (или рассеяния) значений СВ, поэтому часто называется дисперсией и обозначается D_х . Заметим, что можно понимать как средний квадрат центрированной СВ.

Центральный момент третьего порядка (третий центральный момент) равен

, для дискретной СВ;

, для непрерывной СВ;

и может пониматься как математическое ожидание куба центрированной СВ.

Центральный момент четвертого порядка (четвертый центральный момент) равен

, для дискретной СВ;

, для непрерывной СВ;

и может пониматься как математическое ожидание четвертой степени центрированной СВ.

Нет смысла продолжать дальше перечисление центральных моментов. Установим связь между начальными и центральными моментами. Для непрерывной СВ

;

разлагая степень скобки в подынтегральном выражении в бином Ньютона:

,

(- число сочетаний из k по s), меняя порядок интегрирования и суммирования:

,

и учитывая, что интеграл в правой части равен , находим

.

(3.4.6)

Полученное равенство показывает, что центральный момент k-го порядка выражается через начальные моменты порядков до k-го включительно. Аналогичным путем то же самое равенство выводится и для дискретных СВ. Из (3.4.6) находим:

,

,

,

(3.4.7)

,

,

...................................................

Первые два равенства нам уже были известны, равенство (3.4.7) исключительно важно и будет в дальнейшем часто использоваться (его необходимо помнить наизусть).

Мы выразили центральные моменты через начальные, теперь, наоборот, выразим начальные моменты через центральные. Для непрерывной СВ, обозначив x-m_x=x⁰ , находим:

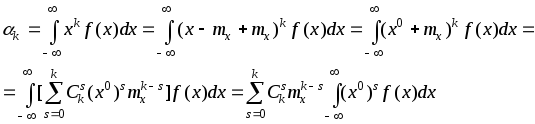
т. е.

.

(3.4.8)

Полученное равенство показывает, что начальный момент k-го порядка выражается через центральные моменты порядков до k-го включительно. Аналогичным путем то же самое равенство выводится и для дискретных СВ. Из (3.4.8) находим:

,

,

,

,

,

...............................................

Первые два равенства нам уже были известны, третье повторяет равенство (3.4.7).