Конспект лекций Глазова / 2.13, 2.14. Посл исп, ф-ла Пуасс

2.13. Последовательные независимые испытания.

Определение 2.13.1. Случайный эксперимент, включающий n>1 последовательных испытаний случайного события А, называется схемой последовательных испытаний. Испытания называются независимыми, если совершения или несовершения события А в одних испытаниях не влияют на вероятности совершений А в других испытаниях. Испытания называются однородными, если вероятность совершения А в каждом отдельном испытании одинакова.

Схема последовательных испытаний имеет исключительное значение в теории вероятностей и ее приложениях, т. к. большое число теоретически и практически важных задач во всех областях знаний сводится к этой схеме.

Рассмотрим схему последовательных независимых однородных испытаний. Обозначим: n - общее число испытаний, p - вероятность совершения события А в одном испытании, q=1-p - вероятность несовершения А в одном испытании. Поставим вопрос: какова вероятность P_nm , что событие А совершится ровно m (m=0, 1, 2, ... , n) раз? Ответ дается биномиальной формулой

,

(2.13.1)

где - число сочетаний из n по m.

Вывод формулы. Вероятность того, что событие А совершится в m заданных испытаниях и, следовательно, не совершится в остальных n-m испытаниях, равна p^mq^n-m; эти m заданных испытаний можно выбрать способами, представляющими собой несовместные события. Искомая вероятность относится к событию, равному сумме указанных событий, и вследствие их несовместности равна сумме их вероятностей, что и дает (2.13.1).

Биномиальная формула на самом деле дает ответы на n+1 поставленных вопросов: Р_n1 , P_n2 ,..., P_nn . Рассмотрим частные случаи формулы.

1) Вероятности того, что А совершится во всех испытаниях:

,

и не совершится ни в одном испытании:

,

могут быть вычислены непосредственно по формуле вероятности произведения независимых событий.

2) Вероятность совершения события А точно один раз

отнюдь не равна вероятности р совершения А в одном испытании.

3) Если p=q=1/2, биномиальная формула упрощается:

, p=q=1/2.

(2.13.2)

Упражнение 2.13.1. Какова вероятность, что при шести бросаниях монеты выпадет ровно три «герба»?

Решение. Считая, что p=q=1/2, по формуле (2.13.2) находим:

.

В условиях схемы последовательных независимых испытаний часто необходимо решить следующую задачу: какова вероятность, что число совершений события А не меньше m₁ и не больше m₂, где ? Обозначим В_к - событие, состоящее в том, что А выполнилось ровно k раз; очевидно, что В_к и В_s несовместны при любых ks, поэтому

.

Пример 2.13.2. Отвечая электрическому «экзаменатору», студент должен по каждому из 10-ти вопросов выбрать один из четырех предложенных ответов. «Экзаменатор» выставляет «отлично» при правильном ответе на все вопросы, «хорошо» - на 8 или 9 вопросов, «удовлетворительно» - на 6 или 7 вопросов. Какова вероятность Р_пол получить положительную оценку, наугад выбирая ответы по каждому вопросу?

Решение. Очевидно, мы имеем схему последовательных независимых испытаний, в которой А - «правильный ответ на вопрос», p=1/4, q=3/4, n=10, и задача состоит в определении вероятности того, что А выполнится более пяти раз. Находим

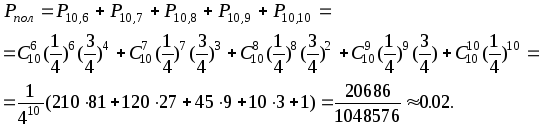
2.14. Поток случайных событий и формула Пуассона.

В теории вероятностей и ее приложениях, в особенности в радиоэлектронике, важное значение имеет формула Пуассона

(2.14.1)

которая исторически появилась (Пуассон, 1837 г.) как асимптотика биномиальной формулы: при и одновременно , ; но в дальнейшем стала играть все возрастающую роль в связи с пуассоновскими потоками.

Определение 2.14.1. Случайным потоком называется последовательность однородных событий, наступающих в случайные моменты времени {t_k}, например, поток термоэлектронов с катода электронной лампы, поток фотоэлектронов с фотокатода, поток отказов аппаратуры, поток зарегистрированных космических частиц и т. д. Случайный поток называется стационарным, если вероятности совершения m событий (m=1, 2, ...) на интервале (t, t+) не зависит от t, а зависит лишь от длины интервала . Говорят, что в потоке отсутствует последействие, если эти вероятности не зависят от того, в какие моменты времени совершались события до интервала (t, t+). Поток называется ординарным, если при вероятность р₂ попадания на (t, t+) двух или более событий есть бесконечно малая более высокого порядка, чем вероятность р₁попадания одного события. Ординарный поток без последействия называется пуассоновским.

В ординарном потоке можно определить плотность потока как предел

при ;

смысл плотности потока - среднее число событий на единицу времени в бесконечно малой окрестности t. В однородном потоке .

Предложение 2.14.1 (без доказательства). В пуассоновском потоке вероятность попадания точно k событий на интервал (t, t+) определяется формулой Пуассона

(2.14.2)

где

.

(2.14.3)

В частном случае однородного потока и (2.14.2) принимает вид

.

(2.14.4)

В частности, вероятность того, что в однородном потоке на интервале длиной Т не произойдет ни одного события, как следует из (2.14.4), равна

(2.14.5)

т. е. экспоненциально падает с увеличением длины интервала.

Пример 2.14.1. Радиоаппаратура некоторого комплекса отказывает в среднем раз в 1000 часов. Найти вероятности следующих событий:

а) хотя бы одного отказа за 100 часов;

б) ровно двух отказов за 200 часов.

Решение. Считая случайный поток отказов однородным пуассоновским, из условия задачи находим =0.001 час^-1; вероятность, что за 100 часов не будет ни одного отказа, найдем по (2.14.5):

,

отсюда вероятность хотя бы одного отказа за 100 часов

Вероятность ровно двух отказов найдем по (2.14.5):