Вспомогательная таблица

Левый интервал	825	855	845	835	845	805	865	825	855	и т.д.
Правый интервал	825	855	845		845				855	и т.д.

Во вспомогательной таблице для примера приведена обработка первых 30 значений табл.1.

Когда возникают трудности в построении рядов распределения для выявления закономерностей из-за значительных ошибок измерения (кривые распределения получаются с значительными провалами или гребенчатые), то можно использовать способ построения ряда распределения по среднему квадратическому отклонению [2].

Для этого определяют эмпирическое значение среднего квадратического отклонения по дискретному или первичному интервальному ряду распределения. Затем от наименьшего значения признака отнимают половину. Это будет новое начало ряда распределения. Все интервалы имеют ширину. Таким образом, левая граница 1-го интервала равна, правая граница 1-го интервала равна, правая граница 2-го интервала будет и т.д. Приможет получиться мало интервалов, тогда следует брать ширину интервалаили. Это требуется при проведении более точных исследований.

В случае крайне неравномерно распределенных по размаху варьирования экспериментальных данных, когда в отдельные интервалы попадает весьма малое количество частот (менее 5), удобно использовать метод равночастотных интервалов [13].

Этот метод основан на условии соблюдении равной частоты (равной вероятности) попадания значений признака в любой из интервалов, т.е.

n=const=m и n_i/n==const.

При этом интервалы получаются разной длины.

На основании объема выборки принимается решение о количестве интервалов (в тех же пределах, что и ранее, т.е. от 6 до 20) и числе значений признака m в интервале, исходя из условий

; .

Ширина каждого интервала выбирается по следующему правилу.

Для первого интервала

.

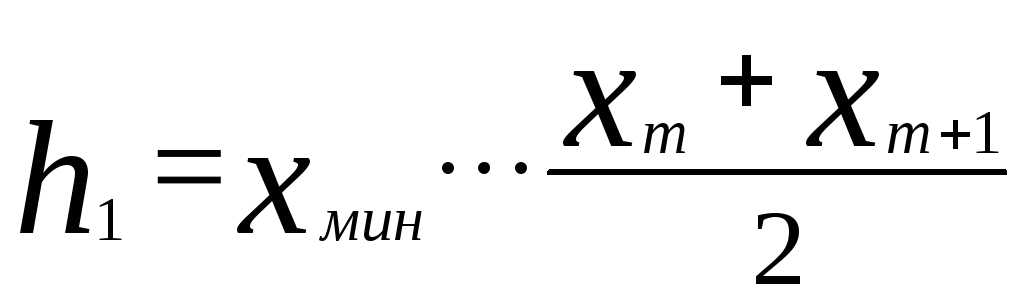Для второго интервала

.

Для i-го интервала

.

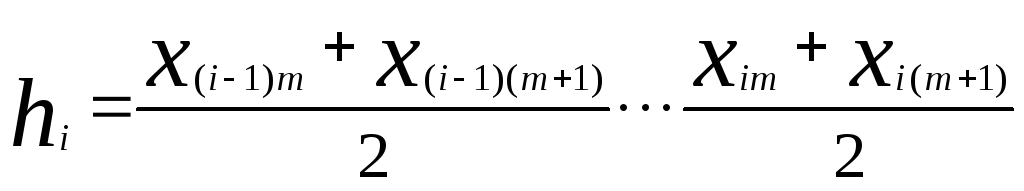Для последнего -го интервала

.

В приведенных выражениях обозначение определяет значение i*m-го признака.

Например, выбрано m=12 = const, i = 5, тогда , т.е. 60-десятое значение признака. Следует заметить, что при этом значения признака должны быть расположены в возрастающем порядке, т.е. должен быть построен вариационный ряд (а иногда и дискретный ряд распределения). Если в вариационном ряде имеется по несколько одинаковых значений признака, тоm надо выбирать так, чтобы все эти одинаковые значения попадали в один интервал, а общее количество значений признака в интервале оставалось неизменным, т.е. частота не превышала выбранное n_i = m = const. Это удобнее делать по дискретному ряду распределения.

В тех случаях, когда , принимаетсятак, что. Разностьвключается в один или два интервала с наибольшей плотностью распределения случайной величины (в интервалы, имеющие меньшую длину).

Отметим, что при использовании приведенного метода гистограмма должна строиться по плотностям распределения частот или частостей.

К достоинствам изложенного метода равночастотных интервалов относится то, что он позволяет рациональным образом группировать данные при выборках небольшого объема.