Теоретическая частость (вероятность) будет равна

,

где и- нормированные отклонения, соответствующие началу и концу интервала. Теоретические частоты определяются по формуле

.

Вычисления проводятся с помощью табл.10. Выравнивание частот проводится по тем же положениям, что и в табл. 8.

Расчёт теоретической интегральной кривой распределения по интервалам удобнее проводить по формуле [2,11 и др.]

, где c - правая граница интервала.

По этой формуле непосредственно определяются значения функции нормального распределения без предварительного вычисления дифференциальной функции распределения. Расчёт приведён в табл. 11.

Значения функций инаходятся в приложении 5. Результаты, найденные в таблице приложения не делить на 2.

Таблица 10

Интервалы									выровненные
795-805	7	0,035	-2,50	-1,87	-0,4940	-0,4695	0,0245	4,9	5,0
805-815	14	0,070	-1,87	-1,25	-0,4695	-0,3945	0,0750	15,0	15,0
815-825	34	0,170	-1,25	-0,63	-0,3945	-0,2355	0,1590	31,8	32,0
825-835	47	0,235	-0,63	0	-0,2355	0	0,2355	47,1	48,0
835-845	44	0,220	0	0,63	0	0,2355	0,2355	47,1	48,0
845-855	33	0,165	0,63	1,25	0,2355	0,3945	0,1590	31,8	32,0
855-865	14	0,070	1,25	1,87	0,3945	0,4695	0,0750	15,0	15,0
865-875	7	0,035	1,87	2,50	0,4695	0,4940	0,0245	4,9	5,0
	200	1,000					0,9880	197,6	200

Таблица 11

Интервалы							выровненные
795-805	-1,87	-0,4695	0,0305	0,035	7	6,1	6
805-815	-1,25	-0,3945	0,1055	0,105	21	21,1	21
815-825	-0,63	-0,2355	0,2645	0,275	55	52,9	53
825-835	0	0	0,5000	0,510	102	100,0	100
835-845	0,63	0,2355	0,7355	0,730	146	147,1	147
845-855	1,25	0,3945	0,8945	0,895	179	178,9	179
855-865	1,87	0,4695	0,9695	0,965	193	193,9	194
865-875	2,50	0,4940	0,9940	1,000	200	198,8	200

Дифференциальная кривая, рассчитанная в табл. 10, представлена на рис. 3.

Плавная интегральная кривая, рассчитанная в табл. 11, не приведена на рис.4 в связи с тем, что масштаб рисунка мелкий, и такая кривая будет почти полностью совпадать с ломаной кумулятивной кривой и скроет её особенности.

После вычисления теоретической кривой распределения и нанесения её на график эмпирического распределения может наблюдаться сдвиг между вершинами или различная острота вершин. Это может быть обусловлено в некоторых случаях ошибками в определении и из-за конечного объёма выборки. Для улучшения совпадения кривых в таких случаях рекомендуется варьировать значениями и в пределах их ошибок, учитывая, что с уменьшением  кривая становится острее.

Следует отметить ошибку, которая встречается при применении нормального закона распределения.

Этот закон часто применяют вместо усечённого нормального закона распределения, получая при этом хорошее согласие с эмпирическим распределением. Ошибка заключается в том, что теоретическую кривую нормального распределения рассчитывают не в пределах 3, а в пределах усечения, отбрасывая произвольно ту часть теоретической кривой, которая выходит за пределы усечения. Поэтому и получается хорошее согласие, что, конечно, неверно. Кривая нормального закона распределения должна начинаться и кончаться на оси абсцисс в пределах 3, опираться на нее, а не быть “подвешенной” над осью абсцисс.

Прежде чем приступать к нанесению теоретической кривой на гистограмму, необходимо определить значения илидля вершины кривой при выбранном значении математического ожидания,а также точки касания ветвями теоретической кривой оси абсцисс.

Для рассматриваемого примера максимум кривой будет при x=a=835. Следовательно,

выровненная .

Точки касания будут иметь значения (при =16):

,

.

Проконтролировать правильное построение теоретической кривой нормального распределения можно путём её вычисления в реперных точках по следующим соотношениям [39]

Для нашего примера

	835	8358	83516	83524	83532	83548
	0,249	0,218	0,155	0,078	0,035	0,003
	50	44	31	15	7	0

Полученные результаты хорошо совпадают с расчётами в табл.8 и 10.

Точки кривой, соответствующие значениям x=a, являются точками перегиба ветвей.

10.2. Распределения, отличные от нормального

Методику определения параметров графическим методом для некоторых распределений, отличных от нормального, можно найти в [14,15,20]. Определение доверительных границ для параметров различных законов распределения рассмотрено в [3, 6, 11, 15, 16, 20 и др.].

При расчётах распределений, отличных от нормального, не следует забывать о том, что в литературе они обычно рассматриваются в пределах от 0 до . Так как на практике распределения могут начинаться с какого-то конкретного значения x, то в формулы для таких распределений вместо x следует подставлять

,

где - новое начало координат. Это положение не относится к логарифмически нормальному и усечённому нормальному законам. Кроме того, в некоторых источниках параметр однопараметрических законов (Рэлея, Максвелла и др.) обозначается через, которое не является в данном случае средним квадратическим отклонением.

Как правило, все рассматриваемые в литературе распределения имеют правостороннюю асимметрию, т.е. левый склон кривой распределения более крутой, чем правый. Однако на практике часто имеет место левосторонняя асимметрия. В этих случаях можно пользоваться известным асимметричным распределением, развёрнутым на 180°, т.е. с так называемыми обращёнными аргументами.

И наконец, следует всегда иметь в виду, что теоретические законы распределения для непрерывных случайных величин, как правило, начинаются и заканчиваются на оси абсцисс, опираются на нее, а не "парят над ней", "не висят в воздухе". Это требует нахождения точек касания ветвями теоретической кривой оси абсцисс.

10.2.1. Усечённое нормальное распределение

Такое распределение получается из нормального распределения путём ограничения изменения случайной величины x одним или двумя пределами - соответственно одностороннее или двустороннее усечённое нормальное распределение.

Плотность и функция распределения определяются по формулам

;

,

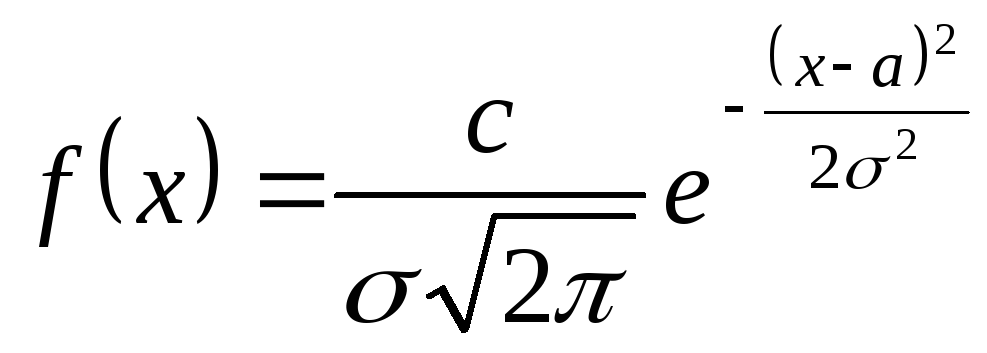где С - нормирующий множитель;

b и d - пределы изменения x;

a и  - математическое ожидание и среднее квадратическое отклонение неусечённого распределения.

Введём нормирующий множитель .

Тогда F(x) будет нормированной функцией распределения

.

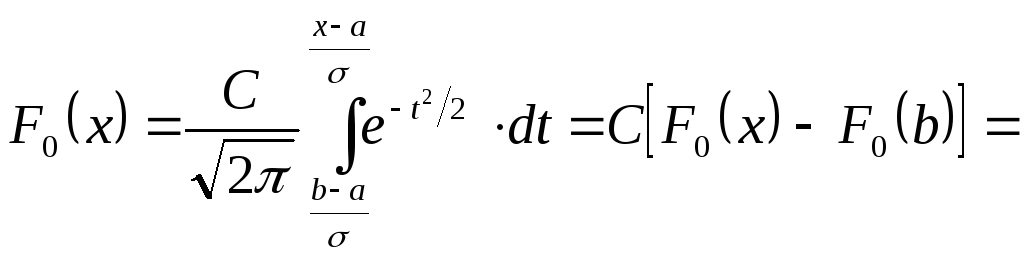
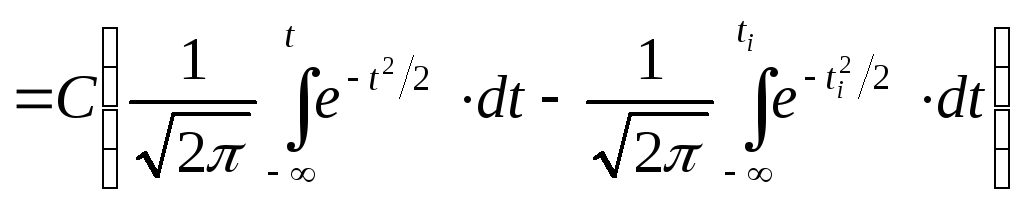Множитель С определяется по формуле

,

где

.

Функция Лапласа

;

.

Следует помнить о правиле знаков

F(-x)=1-F(x), Ф(-x)=-Ф(x).

и определяются по таблицам нормального распределения в функции отt.

Для определения параметров распределения математического ожидания и среднего квадратического отклонения используется метод моментов. Согласно [21], имеем

;

,

где

;

- нормированная плотность распределения.

Приравниваем теоретические и эмпирические моменты и находим и из системы уравнений (см. также [25, с.274]):

,

.

В уравнениях известны .