5.3. Основные соотношения параксиальной оптики

Основные соотношения параксиальной оптикисвязывают между собой фокусные расстояния, положение и размеры предмета и изображения, угловое, линейное и продольное увеличения.

5.3.1. Зависимость между положением и размером предмета и изображения

Линейное увеличение: или Формула Ньютона: Формула отрезков или формула Гаусса:

5.3.2. Угловое увеличение и узловые точки

Выражение для вычисления углового увеличения: Узловые точки– это точки, в которых угловое увеличение равно единице.

Чтобы найти узловые точки и, от переднего фокуса откладывается заднее фокусное расстояние, а от заднего фокуса откладывается переднее фокусное расстояние. Отрезкииравны. Если, то узловые точки совпадают с главными.

Линейное и угловое увеличение связаны соотношением:

5.3.3. Частные случаи положения предмета и изображения

Рассмотрим различные положения предмета и изображения (различные и):

• :,,. Предмет и изображение – этоглавные плоскости.

• :,,. Предмет и изображение – этоузловые точки.

• :,,. Предмет находится на двойном фокусном расстоянии.

• :,,. Предмет находится впереднем фокусе, а изображение – в бесконечности.

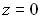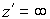• :,,. Предмет находится на бесконечности, а изображение – взаднем фокусе.

5.3.4. Связь продольного увеличения с поперечным и угловым

Продольное увеличение: Угловое увеличение:

Если оптическая система находится в однородной среде (), то:,.

5.3.5. Диоптрийное исчисление

Диоптрийное исчисление– это измерение продольных отрезков в обратных единицах (диоптриях):,, где– приведенная длина. Одна диоптрия соответствует приведенному отрезку в 1м. Если отрезок измеряется в мм, то обратный отрезок измеряется в килодиоптриях.

Соотношение для приведенных отрезков в пространстве предметов () и изображений () иоптической силы, измеряемых в диоптриях:

5.3.6. Инвариант Лагранжа-Гельмгольца

Инвариант Лагранжа-Гельмгольца связывает линейный размер предмета и угловой размер пучка лучей. Эта величина инвариантна, то есть неизменна в любом пространстве:

Инвариант Лагранжа-Гельмгольца характеризует информационную емкость оптической системы, то есть величину пространства, которое может быть отображено оптической системой. Этот инвариант математически выражает закон сохранения информации в геометрической оптике