Atomnaya_fizika_UP

51

2. В квантовой механике теряет смысл деление полной энергии (Е) на кинетическую ( EK ) и потенциальную ( En ). EK зависит

от импульса, En — от координат частицы, одновременно они не

могут иметь точное значение, можно измерять только полную энергию частицы. (Можно только удивляться прозорливости Эйнштейна, который в своей специальной теории относительности — 1905 г.! — пользовался только понятиями полной энергии

иэнергии покоя).

3.Понятие траектории к микрочастицам, строго говоря, неприменимо из-за наличия у них волновых свойств. В теории атома это означает отказ от понятия «орбиты». Можно говорить лишь о локализации электрона в пределах атома и различных квантовых значениях энергии.

4.Именно соотношение неопределенностей позволило ответить на мучавший столь долго Резерфорда и других вопрос: «почему электрон не падает на ядро?» Диаметр атома примерно

10−10 м, диаметр ядра 10−15 м. Если электрон упадет на ядро, то

неопределенность его координаты уменьшится в 105 раз. Во столько же должна возрасти неопределенность импульса (см. 3.3.1) и, следовательно, величина самого импульса, а это противоречит закону сохранения импульса. Атом — замкнутая система, и без воздействия извне электрон не сможет упасть на ядро. Для «вдавливания» электрона в ядро требуются огромные силы, и пока в природе это реализовано только в нейтронных звездах. (После того как прекратятся термоядерные реакции в звездах, массы которых в несколько раз превышают массу Солнца, мощные гравитационные силы сжимают вещество звезды, электроны атомов вдавливаются в ядра, протоны, взаимодействуя с электронами, превращаются в нейтроны. Диаметры таких звезд не превышают несколько десятков километров, и они вращаются с огромной угловой скоростью — пульсары).

3.3.2 Электроны в электронно-лучевой трубке

Существуют, однако, ситуации, когда понятием «траектория микрочастицы» пользоваться допустимо.

52

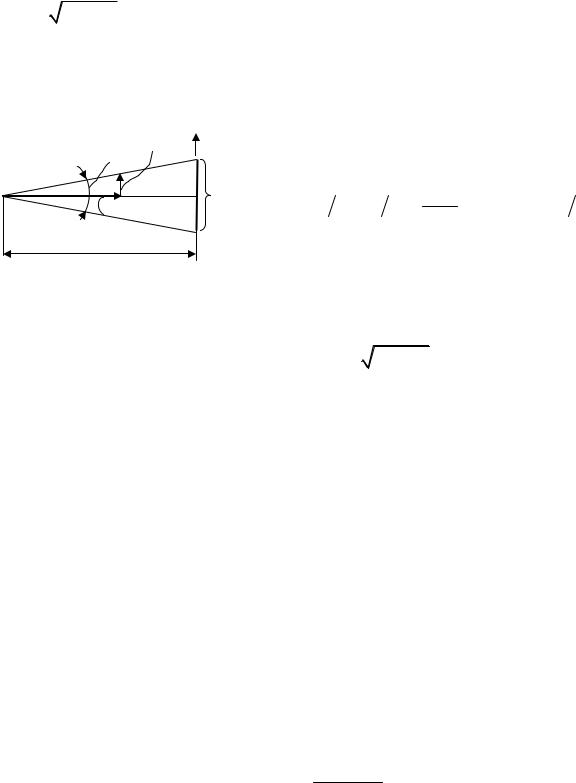
Рассмотрим движение электронов в электронно-лучевой трубке (ЭлТ). Импульс электронов вдоль оси трубки (вдоль луча) определяется величиной ускоряющего напряжения U:

Po = 2meU . Пусть с помощью фокусирующих устройств нам

удалось получить диаметр луча на экране (диаметр пятна) d =10 мкм. Найдем неопределенность координаты электрона x , обусловленную волновыми свойствами электрона. Неопределен-

θрисунок):x

=2,75 10−2 мкм 0,03 мкм. Это число много меньше реального

размытия луча d (из-за кулоновского отталкивания электронов друг от друга), и движение электрона в таких условиях можно рассматривать по классическим законам.

Это — общая закономерность: волновые свойства микрочастиц проявляются тем сильнее, чем меньше область локализации частиц; практически, когда область локализации сравнима с размером атома.

3.3.3 Естественная ширина спектральных линий атома

Спектроскописты давно обратили внимание на тот факт, что спектральные линии были шире, чем это допускала погрешность спектроскопических приборов. Большая ширина спектральных линий (рис. 3.3, а) противоречила и теории Бора, по которой час-

тота спектральной линии ωo = En − Eк . Поскольку En и Eк

должны быть точной величиной, и спектральная линия должна быть узкой, насколько это позволял спектральный прибор.

53

0,5Jm

Рис. 3.3

а— наблюдаемая интенсивность спектральных линий;

б— к объяснению ширины спектральных линий

Объяснение этому факту дало соотношение неопределенностей E t ≥ 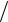2 (см. 3.3.2). Атомы испускают фотоны, переходя

из возбужденного состояния в другое возбужденное или основное (стационарное). Например, для атома водорода состояние с n =1 — основное, в нем электрон может находиться сколь угодно долго, все другие состояния с n ≥ 2 — возбужденные: n = 2 — 1-е возбужденное, n = 3 — 2-е возбужденное и т.д. Среднее время

жизни атома в возбужденном состоянии τ ≈10−8 c, после чего атом (по теории Бора — электрон) переходит самопроизвольно в

тат хорошо согласуется с измерениями ширины спектральной линии. Эта ширина есть следствие корпускулярно-волнового дуализма электронов — фундаментального свойства всех микрочастиц, поэтому ее называют естественной шириной спектральных линий: ни уменьшить, ни избавиться от нее нельзя. Поскольку

54

Δλ = hc . Нужно приравнять относительные величины неопреде-

3.3.4 Принцип дополнительности Бора

Одновременно с формулировкой соотношения неопределенностей В.Гейзенбергом Н.Бор, тяготеющий к философским обобщениям, сформулировал принцип дополнительности. В нем утверждается, что в любом опыте с микрочастицами наблюдатель получает информацию не о «свойствах объектов самих по себе», но о свойствах объектов в связи с конкретной ситуацией, включавшей в себя и измерительные приборы. Информацию, полученную при данных условиях, следует понимать как дополнительную к информации, полученной при других условиях. Существенно, что сведения, полученные при разных условиях, нельзя простым образом складывать; они отражают разные (дополнительные друг другу) стороны единой реальности. Принцип дополнительности находит прямое выражение в корпускулярноволновом дуализме. Микрочастица не является ни корпускулой, ни волной, но в то же время мы пользуемся для описания микрообъекта этими двумя взаимно исключающими друг друга образами.

Частица-волна — две дополнительные стороны единой сущности. Импульс и координаты ограничивают, но и дополняют друг друга. Полнота описания природы только в понимании дополнительности понятий: физическая картина явления и его математическое описание дополнительны. Попытка точного математического описания затрудняет ясное понимание. «Что дополнительно понятию истины? — ясность», — говорил Н. Бор.

55

3.4 Волновое уравнение Шрёдингера

Развивая идеи де-Бройля о волновых свойствах вещества, Шрёдингер нашел свое знаменитое уравнение и создал теорию, которая называется сейчас «квантовой механикой».

Отличие уравнения Шрёдингера от волны де-Броля состояло в том, что оно описывало поведение частицы во внешнем силовом поле. Теория Шрёдингера — феноменологическая теория, т.е. не фундаментальная и не отвечает на некоторые вопросы «Почему именно так?». В настоящее время есть точная теория атомных и молекулярных явлений — квантовая электродинамика, разработанная в 40-е и 50-е годы прошлого века Глэшоу, Фейнманом и Швингером. Теория Шрёдингера — первое приближение к квантовой электродинамике, она значительно проще и верно описывает основные свойства атомов и молекул.

Теория Шрёдингера основана на некоторых допущениях, главные из которых:

1.Частицы не рождаются и не исчезают; в любом физическом процессе число частиц данного типа остается неизменным. Следовательно, теория не пригодна для описания ядерных процессов.

2.Скорость частиц много меньше скорости света, т.е. теория Шрёдингера — нерелятивистская теория. (Релятивистский вариант уравнения Шрёдингера был получен П.Дираком в 1927 г.).

Уравнение Шрёдингера — основное уравнение квантовой механики (аналог второго закона Ньютона в классической механике). Это общее уравнение, пригодное для решения всех задач (с указанными выше ограничениями).

Нестационарное уравнение Шрёдингера

функция координат и времени, имеющая смысл эффективного потенциала внешнего силового поля, в котором движется части-

ца; i = −1 — мнимая единица, ее присутствие говорит о том, что

56

(3.4.1) — волновое уравнение; ψ( x, y, z,t) — пси-функция, функ-

ция характеризующая состояние микрочастицы. Решая уравнение Шрёдингера, находят именно ψ-функцию, а уж из нее, воз-

действуя соответствующими операторами, находят динамические параметры частицы (импульс, момент импульса и т.д.).

Если силовое поле, в котором движется частица, стационарно, то потенциал не зависит от времени и функция U имеет смысл потенциальной энергии взаимодействия силового поля и частицы. В этом случае ψ-функция распадается на два множите-

ля, один из которых зависит только от координат, другой — толь-

учтя, что (−i2 =1), получим

Это стационарное уравнение Шрёдингера. Поскольку в дальнейшем мы будем пользоваться только им, запишем его в более традиционной форме, учтя, что ψ1 ≡ ψ:

3.5 Физический смысл ψ-функции

Сам Шрёдингер пытался описать частицу как суперпозицию нескольких волн — волновой пакет. Но это неверно: волновой пакет довольно быстро расплывается, а частица живет долго. Правильный физический смысл ψ-функции дал М. Борн (1882—

1970 гг.) в 1926 г.

Вероятностное толкование волновой функции проглядывает в следующем рассуждении. При дифракции света различные точ-

57

ки экрана освещены по разному: интенсивность света пропорциональна квадрату амплитуды световой волны. Если смотреть на свет как на поток частиц, то перераспределение интенсивности — это разная вероятность попадания фотонов в разные точки экрана: чем больше интенсивность света, тем бóльшая вероятность прилёта сюда фотона. Отсюда ясна связь между вероятностью и квадратом амплитуды световой волны. Рассмотрим более строго эти представления.

К любой волновой функции предъявляется ряд требований — они должны удовлетворять так называемым стандартным условиям:

1) ψ-функция должна быть однозначной, непрерывной,

гладкой и конечной (за исключением, может быть, отдельных точек);

2) она должна иметь непрерывную и конечную производ-

ную.

Есть и еще одно требование — чисто физическое — усло-

вие нормировки:

3) если частица существует, то вероятность ее нахождения в объеме от −∞ до + ∞ должна быть равна единице.

где Р — вероятность нахождения частицы, ψ* — комплексно сопряженная функция. Вообще, вероятность обнаружения частицы

в бесконечно малом объеме dV dP = A ψ 2 dV , для нормирован-

Квадрат модуля ψ-функции есть плотность вероятности

нахождения частицы в каком-либо месте пространства (вероятность нахождения частицы в единице объема пространства).

Из смысла ψ-функции следует, что квантовая механика

имеет статистический (вероятностный) характер. (Кстати — в матричной механике то же самое: интенсивность спектральных линий пропорциональна вероятности соответствующих перехо-

58

дов электронов в атоме). С вероятностным толкованием законов микромира не соглашался Эйнштейн: «Я не могу допустить, что Господь Бог играет в кости». Известна многолетняя полемика по этому вопросу между А.Эйнштейном и Н.Бором.

Квантовая механика дает совершенно особую концепцию движения — не по траекториям. Движение по траектории делает возможным однозначное предсказание будущего по прошедше-

му. В квантовой механике предсказание носит вероятност-

ный характер. «Проблема понимания квантовой механики только в том, что мы больше не имеем права детально описывать поведение частиц в пространстве» (Р. Фейнман). Разумеется, это не означает отказа от закономерностей движения, просто законы эти — статистические, вероятностные.

Вернемся еще раз к дифракции световых волн. Когерентные волны, складываясь, могут взаимно погашаться, когда они в противофазе. Но вероятности попадания электрона в ту или иную точку экрана погашаться не могут: вероятность — величина положительная (изменяется от 0 до 1). Точно так же при дифракции света погашаются не интенсивности света (интенсивность — энергия, переносимая волной через единицу площади за единицу времени, величина положительная), складываются или вычитаются только напряжённости электромагнитных полей, т.е. амплитуды колебаний. Аналогично у электронов — погашаются амплитуды вероятностей нахождения в какой-либо точке пространства. Только амплитуды, а не вероятности могут обладать волновыми свойствами.

Теперь можно ответить на вопрос, что колеблется при движении микрочастицы? Амплитуда вероятности ее нахождения в данной точке пространства. Волна де-Бройля — волна вероятности. Волновое уравнение Шрёдингера описывает поведение в пространстве и времени вероятности нахождения частицы.

На фундаментальном уровне частицы материи имеют двойственную природу, а переход из одного состояния в другое носит вероятностный характер и происходит скачками. В классической механике статистические закономерности проявляются лишь для большой совокупности частиц. В квантовой механике в поведе-

нии отдельной частицы уже проявляется элемент случайности.

59

«В квантовой механике понятие вероятности есть понятие первичное, оно играет фундаментальную роль» (В.А. Фок).

3.6 Квантование энергии частицы в одномерной потенциальной яме

Из уравнения Шрёдингера и условий, налагаемых на ψ-функ- цию, непосредственно вытекают правила квантования энергии. Квантовые условия Бора являются гениальной, но догадкой, причем удовлетворяющей не во всех случаях. Великое открытие Шрёдингера состояло в том, что если принять волновые представления о веществе, а это доказано экспериментом, то получается естественный и общий способ квантования.

В уравнение Шрёдингера в качестве параметра входит полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения типа Шрёдингеровского (комплексные) имеют решения, удовлетворяющие стандартным условиям, не при любых значениях x, параметра Е, а лишь при некоторых, называемых собственными. Функция, соответствующая собственному значению параметра, называется собственной функцией.

Нахождение собственных значений представляет весьма трудоемкую задачу. Мы рассмотрим самый простой пример: найдем собственные значения Е и соответствующие им собственные функции для частицы, находящиеся в бесконечно глубокой одномерной потенциальной яме. Частица может двигаться только вдоль оси x. Движение ограничено непроницаемыми для частицы стенками (рис. 3.4, а).

Рис. 3.4

а — схема потенциальной ямы; б — распределение собственных значений энергии частицы в яме

60

Потенциальная энергия ямы (U) имеет следующий вид: при

Вероятность обнаружить частицу за пределами потенциальной ямы (где U = ∞) равна нулю, следовательно, там и ψ = 0. Из ус-

ловий непрерывности и гладкости волновой функции следует, что и на границах ямы

(3.6.2)

Итак, частица может находиться только внутри ямы, где U = 0, следовательно, 3.6.1 будет

нельзя положить равным нулю, т.к. (см. 3.6.4) ни одна из величин, входящих в выражение для K , не может быть равной нулю ( E ≠ 0, т.к., как минимум, есть энергия покоя частицы). Остается положить

(n = 0 тоже не подходит, т.к. при этом K ≡ 0 ). Теперь можно получить собственные значения энергии частицы. Из (3.6.4):