Эксперимента для устройств, характеризуемых двумя (а) и тремя (б) первичными факторами

Для устройства, характеризуемого тремя первичными факторами х₁,х₂, х₃с номинальными значениями факторамих₁₀,х₂₀,х₃₀, факторное пространство для k= 3 можно представить в виде куба (рисунок 3.12,б) [12-14].

Восемь экспериментальных точек в вершинах куба соответствуют всевозможным сочетаниям нормированных уровней факторов. Тем самым обеспечивается рациональный «обзор» факторного пространства в окрестности номинальной точки, соответствующей началу координат.

Правило перехода от коэффициентов В, которые получаются из опыта, к коэффициентам β в натуральном масштабе при использовании полиномов первого порядка эти правила достаточно простые [13, 20]:

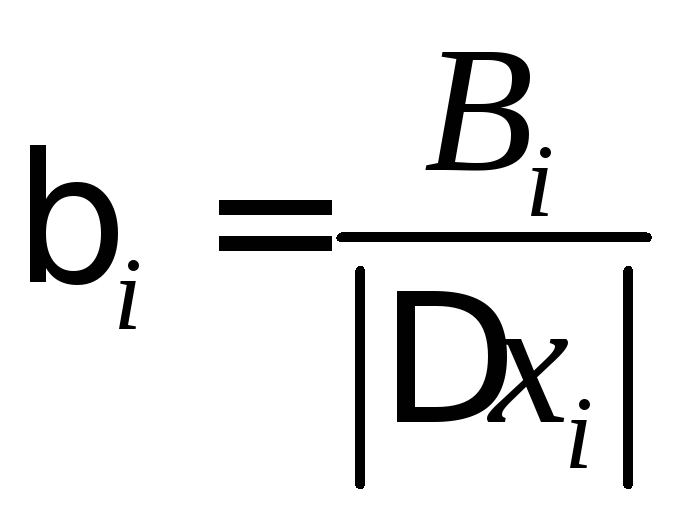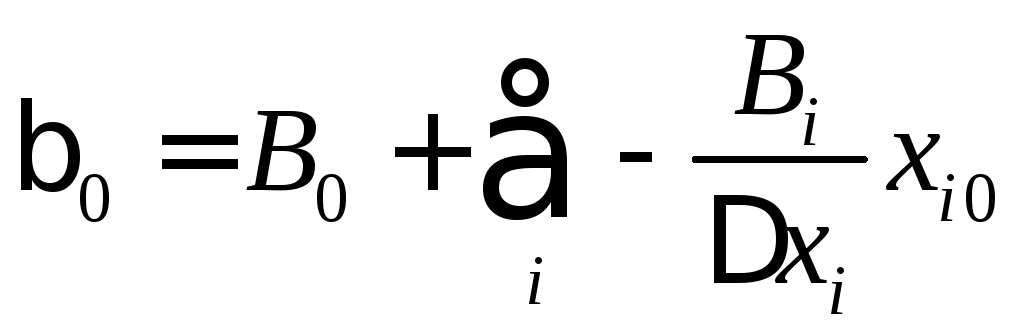; .(3.15)

Иногда используют насыщенный планфакторного эксперимента, в котором количество переменных точно соответствует количеству опытов. Насыщенный план обладает рядом ограничений, обусловленных тем, что в нем нет избыточности. Поэтому в эксперимент обычно целесообразно вводить избыточность, то есть увеличение количества опытов по отношению к количеству переменных, для того чтобы кроме вычисления коэффициентов линейного приближения иметь возможность также оценить ошибку эксперимента, проверить адекватность принятой модели (полинома) результатам эксперимента, оценить значимость коэффициентов полинома. При этом происходит переход к ПФЭ или к ДФЭ.

При оценке значимости коэффициента решается вопрос о необходимости использования при расчете не только коэффициентов B_iпри каждой из переменных, но и коэффициентов, показывающих взаимодействие переменных, т.е. существенность влияния тех коэффициентов β_ijилиB_ij, которые стоят при произведениях переменных.

Наибольшую избыточность в опыт можно внести, осуществляя его 2^праз (N = 2^п), поскольку при этом комбинации изменений переменных не будут повторяться. Матрица планирования такого эксперимента для трех переменных приведена в таблице 3.1. Такие планы называют планами типа 2^п или планами ПФЭ. Для вычисления коэффициентов используются выражения [20]:

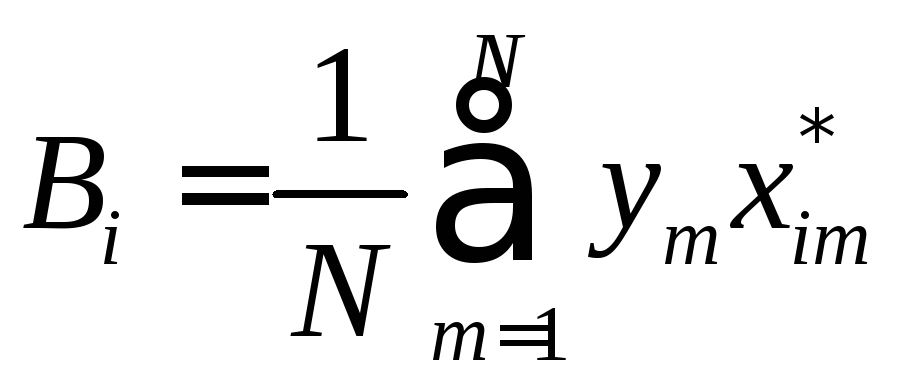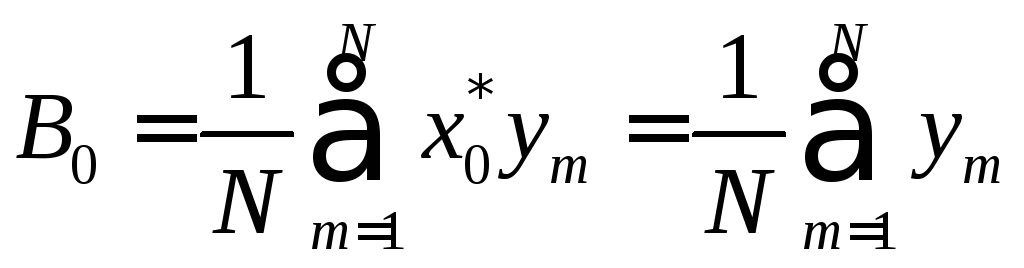; (3.16)

Таблица 3.1 – Матрица планирования ПФЭ 2^п для п = 3 (ПФЭ 2³)

m					mОП						ym
1	1	1	1	+1	7	+1	+1	+1	1	+1	у1
2	+1	1	1	+1	2	1	1	+1	+1	+1	у2
3	1	+1	1	+1	5	1	+1	1	+1	+1	у3
4	+1	+1	1	+1	3	+1	1	1	1	+1	у4
5	1	1	+1	+1	4	+1	1	1	+1	+1	у5
6	+1	1	+1	+1	6	1	+1	1	1	+1	у6
7	1	+1	+1	+1	8	1	1	+1	1	+1	у7
8	+1	+1	+1	+1	1	+1	+1	+1	+1	+1	у8

Дисперсия коэффициентов B_i:

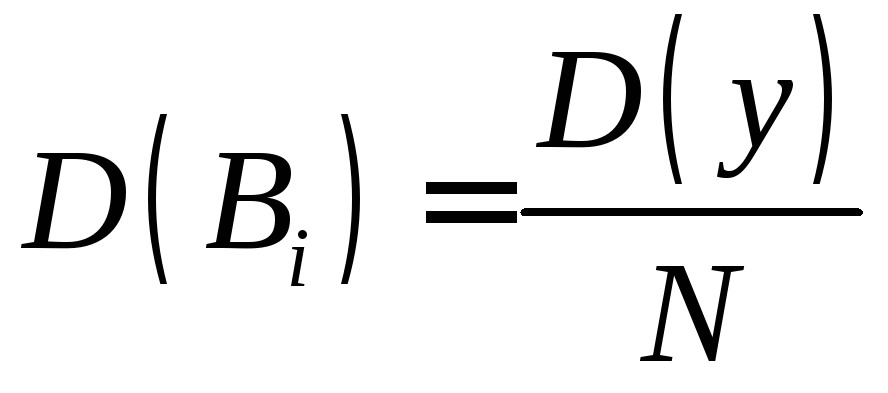; N= 2^п (3.17)

обратно пропорциональна числу опытов N. При избыточности число опытовNувеличивается, что в соответствие с формулой (3.17), приводит к улучшению точности определения коэффициентовB_i.

Рассматриваемый план в соответствие с теорией эксперимента рандомизирован, поскольку в нем переменные изменяются в разных сочетаниях, и опыты производятся не в последовательности строк, а в случайной последовательности, отображенной в столбце m_ОП. Под рандомизацией здесь понимается уравнивание влияния внешних факторов на результаты эксперимента.

Избыточность можно использовать для увеличения количества вычисляемых коэффициентов, т.е. для увеличения количества членов полинома, и для статистического анализа полинома и качества эксперимента.

В связи с тем, что имеется 2^попытов, можно вычислить 2^пкоэффициентов полиномиальной модели, то есть значительно больше, чем число переменныхп. Помимо членов линейного приближения в полином могут быть введены члены, которые описывают взаимодействие, то есть коэффициенты при произведениях переменных в разных сочетаниях. Из таблицы 3.1 следует, что сочетания символов «+» и «» в столбцах при произведениях не повторяют сочетания в столбцах для переменных. Следовательно, имеется возможность вычисления коэффициентов взаимодействия в рассматриваемом примере при четырех произведениях. Для этого используется соответствующее правило, например, для взаимодействия 2-го порядка [20]:

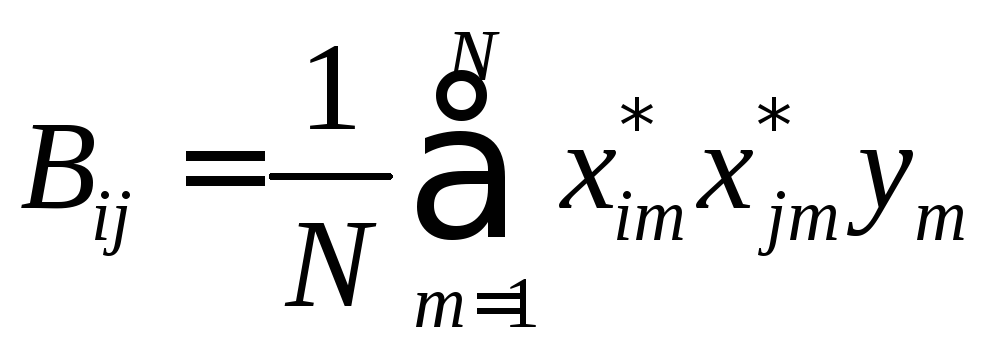. (3.18)

Таким образом, по результатам ПФЭ можно получить неполный полином 2-го порядка. Очевидно, что получение коэффициентов при из результатов ПФЭ невозможно, так как сочетание символов в столбцебудет таким же, как в столбце фиктивной переменной, которая отображает необходимость вычисления постоянного члена полинома.

Для рассматриваемого примера при постановке ПФЭ необходимо провести восемь вариантов опытов, последовательность проведения которых рандомизируется в соответствие со столбцом m_ОП. В столбцеу_т записываются замеренные значения выходного параметра математической модели радиоэлектронного устройства. По полученным значенияму_т могут быть вычисленыВ₀,В₁,В₂,В₃,В₁₂,В₁₃,В₂₃,В₁₂₃. При этом избыточность использована полностью.

В другом варианте по этим же результатам эксперимента могут быть вычислены только В₀,В₁,В₂,В₃. Тогда будет избыточность, которая может быть использована для статистического анализа полинома и качества эксперимента.

Использование избыточности, содержащейся в ПФЭ, для увеличения количества вычисляемых коэффициентов, особенно при большом числе переменных, обычно нецелесообразно. В связи с этим, важное место занимают методы сокращения количества опытов по сравнению с ПФЭ, которые должны предусматривать единообразие и объективную оценку последствий такого сокращения, например методика планирования ДФЭ.

Если количество экспериментов сделать меньше чем 2^п, то целый ряд коэффициентов, описывающих взаимодействие в полиноме, не может быть вычислен. Когда эти взаимодействия значимы, они отображаются в других коэффициентах, и происходит так называемое смешивание. Поэтому основная задача планирования ДФЭ состоит в составлении такого варианта плана, который бы предусматривал значительное уменьшение количества опытов по сравнению с ПФЭ, но приводил бы к смешиванию коэффициентов, которые заведомо не должны быть значимыми.