
- •1.1.1. Понятие множества
- •1.1.2. Способы задания множеств
- •1.1.3. Основные определения
- •1.1.4. Диаграммы Эйлера – Венна
- •1.1.5. Операции над множествами
- •1.1.6. Системы множеств
- •1.1.7. Законы алгебры множеств
- •1.1.8. Решение задач 1-3 контрольной работы № 1
- •1.1.9. Контрольные вопросы и упражнения
- •1.2.1. Декартово произведение множеств. Соответствие множеств
- •1.2.2. Определение бинарного отношения
- •1.2.3. Способы задания бинарного отношения
- •1.2.4. Свойства бинарных отношений
- •1.2.5. Отношения эквивалентности
- •1.2.6. Отношения порядка
- •1.2.7. Частично упорядоченные множества
- •1.2.8. Диаграммы Хассе
- •1.2.9. Изоморфизм частично упорядоченных множеств
- •1.2.10. Решение задач 5,6 контрольной работы № 1
- •1.2.11. Контрольные вопросы и упражнения
- •1.3 Реляционная алгебра
- •1.3.1. Применение отношений для обработки данных
- •1.3.2. Теоретико-множественные операции реляционной алгебры
- •1.3.3. Специальные операции реляционной алгебры
- •1.3.4. Решение задачи 7 контрольной работы № 1
- •1.4. Конечные и бесконечные множества
- •1.4.1. Равномощные множества
- •1.4.2. Классы равномощных множеств
- •1.4.3. Сравнение множеств по мощности
- •1.4.4. Свойства конечных множеств
- •A b c
- •1.4.5. Определение счетного множества
- •1.4.6. Свойства счетных множеств
- •1.4.7. Несчетные множества
- •1.4.8. Булеан бесконечного множества. Выводы
- •1.4.9. Решение задач 8,9 контрольной работы 1
- •1.4.10. Контрольные вопросы и упражнения
1.4.4. Свойства конечных множеств
Множество
Xназываетсяконечным, если
существует биекция
![]() ,
т.е. множествоXможно взаимно однозначно отобразить
на отрезок натурального ряда {1,2,…,n};
при этомX=
n.
,
т.е. множествоXможно взаимно однозначно отобразить
на отрезок натурального ряда {1,2,…,n};
при этомX=
n.
Все множества, для которых такую биекцию установить невозможно, будем называть бесконечными.
Пустое множество принято относить к конечным множествам и обозначать =0.
Сформулируем свойства конечных множеств в виде теорем (не все теоремы будут строго доказаны).
Теорема(правило суммы). Пусть множествоXявляется объединениемrнепересекающихся конечных множеств![]() .
Тогда
.
Тогда![]() .
.
Согласно
условию теоремы система множеств
![]() является разбиением множестваX.
Доказательство проведем методом
математической индукции по числуrблоков разбиения.
является разбиением множестваX.
Доказательство проведем методом
математической индукции по числуrблоков разбиения.
Шаг
1. Покажем, что теорема справедлива
при![]() .
Пусть
.
Пусть![]()
и множества
и множества![]() конечны, т.е. существует биекция
конечны, т.е. существует биекция
![]() и
и
![]() .
Установим биекцию
.
Установим биекцию
![]() следующим образом: всем элементам
множества
следующим образом: всем элементам
множества![]() оставим
прежние номера, а номера элементов
множества
оставим
прежние номера, а номера элементов
множества![]() увеличим на число
увеличим на число![]() .
Полученное отображение
.
Полученное отображение
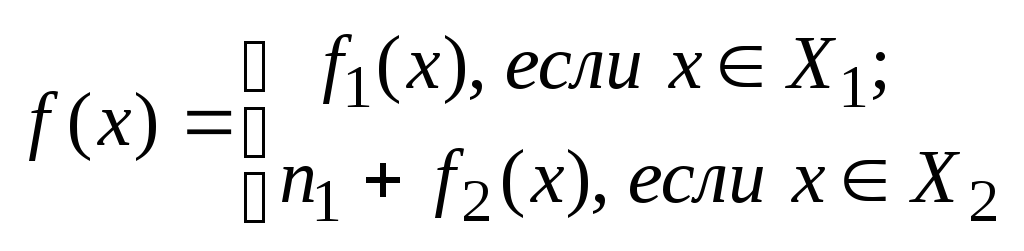
является биекцией
![]() в
силу биективности
в
силу биективности![]() и
и![]() .
Следовательно,
.
Следовательно,![]() .
Основание индукции доказано.
.
Основание индукции доказано.
Шаг
2 . Индукционный переход заключается
в следующем: предположим, что теорема
справедлива при числе блоков разбиения![]() ;
докажем, что в этом случае она будет
справедлива и при числе блоковr.
;
докажем, что в этом случае она будет
справедлива и при числе блоковr.
Предположение:
множества
![]() ,
конечны и образуют разбиение множестваY.
Тогда
,
конечны и образуют разбиение множестваY.
Тогда![]()
Рассмотрим
разбиение множества Xнаrконечных множеств. Тогда![]() по закону ассоциативности объединения.
Обозначим
по закону ассоциативности объединения.
Обозначим![]() Опираясь
на основание индукции (шаг 1), имеем
Опираясь
на основание индукции (шаг 1), имеем
![]() ,
а по индукционному предположению
,
а по индукционному предположению![]() Индукционный переход доказан.
Индукционный переход доказан.
Заключение. Согласно методу математической индукции, теорема справедлива для любого натурального числаr блоков разбиения.
Теорема(правило произведения). Пусть конечное
множествоXпредставлено в виде декартова произведенияrконечных множеств
![]() .
Тогда
.
Тогда![]() .
.
Правило произведения доказывается методом математической индукции аналогично правилу суммы.
Теорема( о мощности булеана конечного множества).
Пусть множествоXконечно и![]() .
Тогда
.
Тогда![]() .
.
Напомним, что B(X)есть булеан множестваX, т.е. множество всех подмножеств множестваX. При построении булеана в 1.1.8 мы использовали эту теорему без доказательства.
Доказательство.
МножествоXконечно, значит, существует биекция![]() .
Зафиксируем порядок элементов множества
.
Зафиксируем порядок элементов множества![]() и рассмотрим множествоVвсех упорядоченных наборов длиныn,
состоящих из нулей и единиц:
и рассмотрим множествоVвсех упорядоченных наборов длиныn,
состоящих из нулей и единиц:
![]() .
.
Установим
взаимно однозначное соответствие
(биекцию)
![]() следующим
образом: элементу
следующим
образом: элементу![]() сопоставляем
множество
сопоставляем
множество![]() ,
содержащее те и только те элементы
,
содержащее те и только те элементы![]() ,
для которых
,
для которых![]() .
Легко проверить, что данное соответствие
является биекцией. Таким образом,
множествоV
и
.
Легко проверить, что данное соответствие
является биекцией. Таким образом,
множествоV
и![]() равномощны. Но множество
равномощны. Но множество![]() Vявляется декартовым произведениемnодинаковых сомножителей
Vявляется декартовым произведениемnодинаковых сомножителей![]() ,
т.е.
,
т.е.![]() и по теореме о мощности произведения
и по теореме о мощности произведения![]() ,
следовательно, и
,
следовательно, и![]() .
.
Теорема(правило включения – исключения). Пусть![]() и
и![]() конечные множества. Тогда
конечные множества. Тогда![]() .
.
Доказательство
теоремы опирается на правило суммы.
Представим множество
![]() в виде объединения непересекающихся
множеств
в виде объединения непересекающихся
множеств![]() ,
где
,
где![]() ,
,![]() ,
,
![]() (рис. 1.23). Тогда по правилу суммы
(рис. 1.23). Тогда по правилу суммы![]() ,
но
,
но
![]() ,
поэтому
,
поэтому![]() ,
,
![]() .
Имеем
.
Имеем![]() ,отсюда
,отсюда![]()
![]()
![]() .
.
