Тема 1. Модель Василия Леонтьева многоотраслевой экономики (балансовая модель)

Модель многоотраслевой экономики была разработана в 1936 году американским экономистом Василием Леонтьевым. Модель Леонтьева применяется в макроэкономике и связана с ведением многоотраслевого хозяйства.

Целью построения данной модели является выяснение объема производства каждой из отраслей производства, который бы удовлетворял все потребности в продукции этой отрасли. При этом каждая отрасль выступает как производитель продукции и как потребитель продукции, произведенной в этой и в других отраслях производства.

Предположим, что рассматривается отраслей экономики. Вся произведенная этими отраслями продукция частично идет на внутреннее потребление, а другая (конечная) предназначена для внутреннего и общественного производства.

Рассмотрим период в 1 год. Введем обозначения:

- общий (валовой объем) -ой отрасли производства,

- объем продукции, произведенной - ой отраслью и потребляемой- ой отраслью;

- объем конечного продукта - ой отрасли.

Так как валовой объем продукции - ой отрасли равен суммарному объему продукции, потребляемой отраслями, и конечного продукта, то справедливо равенство:

которое называется соотношением баланса.

Будем рассматривать модель в стоимостном выражении. Введем коэффициенты прямых затрат:

Коэффициент прямых затрат показывает затраты - ой отрасли на производство единицы продукции- ой отрасли. В некотором промежутке времени коэффициент прямых затрат - постоянная величина. Следовательно, материальные затраты и валовой выпуск имеют линейную зависимость:

В этом случае соотношение баланса примет вид:

В соответствии с экономическим смыслом задачи прии. Обозначим:

- вектор валового выпуска; - вектор конечного продукта;

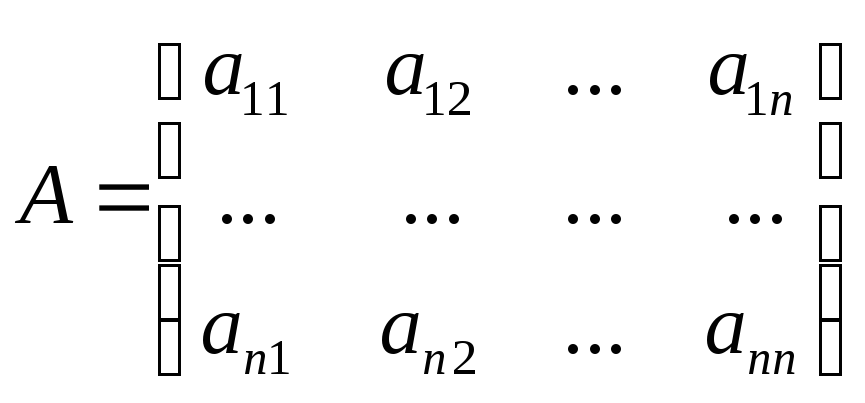- матрица прямых затрат. Тогда систему соотношений баланса можно записать в матричном виде:

Основная задача межотраслевого балансасостоит в отыскании такого вектора валового выпускаХ, который, при известной матрице прямых затратА, обеспечивает заданный вектор конечного продукта.

Перепишем уравнение в виде: Если матрицане вырождена т.е. тоМатрицаназываетсяматрицей полных затрат. Каждый элемент матрицыпоказывает величину валового выпуска продукции-ой отрасли, необходимую для обеспечения выпуска единицы конечного продукта-ой отрасли.

Матрица называетсяпродуктивной, если для любогосуществует решение матричного уравнения. В этом случае и модель Леонтьева называетсяпродуктивной.

Критерий продуктивности матрицы: все элементыматрицынеотрицательны;и существует столбецтакой, что

Контрольное задание №1

В таблице приведены данные об использовании баланса за отчетный период (в условных денежных единицах):

Вариант 1						Вариант 2
Производство	Потребление			КП		Производство	Потребление			КП
	A	B	C				A	B	C
A	50	60	80	60		A	40	18	25	21
B	25	90	40	25		B	16	9	25	16
C	25	60	40	35		C	80	45	50	75

Вариант 3						Вариант 4
Производство	Потребление			КП		Производство	Потребление			КП
	A	B	C				A	B	C
A	18	30	25	1		A	150	180	240	60
B	45	90	20	20		B	75	270	120	25
C	36	36	50	30		C	75	180	120	35

Вариант 5						Вариант 6
Производство	Потребление			КП		Производство	Потребление			КП
	A	B	C				A	B	C
A	50	120	80	60		A	40	18	75	21
B	50	180	80	50		B	16	9	75	24
C	25	120	40	35		C	240	135	150	75

Вариант 7						Вариант 8
Производство	Потребление			КП		Производство	Потребление			КП
	A	B	C				A	B	C
A	18	30	50	5		A	150	180	80	30
B	45	90	40	5		B	75	270	40	25
C	72	90	100	4		C	25	60	40	35

Вариант 9						Вариант 10
Производство	Потребление			КП		Производство	Потребление			КП
	A	B	C				A	B	C
A	10	12	16	20		A	40	180	25	21
B	25	90	8	25		B	160	90	250	100
C	25	60	6	35		C	80	450	50	75

Вычислить необходимый объем валового выпуска каждой отрасли, если конечный продукт первой отрасли должен увеличится на 10%, второй отрасли - на 20%, а третьей отрасли- на 30% (КП- конечный продукт).