Вариант 9

Номер предприятия				Номер предприятия
1	7	3,9	12	11	11	7,1	22
2	7	4,2	13	12	12	7,5	25
3	7	4,3	15	13	13	7,8	26
4	7	4,4	17	14	12	7,9	27
5	8	4,6	18	15	13	8,1	30
6	8	4,8	19	16	13	8,4	31
7	9	5,3	19	17	13	8,6	32
8	9	5,7	20	18	14	8,8	32
9	10	6,9	21	19	14	9,6	34
10	10	6,8	21	20	14	9,9	36

Вариант 10

Номер предприятия				Номер предприятия
1	7	3,6	12	11	10	7,2	23
2	7	4,1	14	12	11	7,6	25
3	7	4,3	16	13	12	7,8	26
4	7	4,4	17	14	11	7,9	28
5	7	4,5	18	15	12	8,2	30
6	8	4,8	19	16	12	8,4	31
7	8	5,3	20	17	12	8,6	32
8	8	5,6	20	18	13	8,8	32
9	9	6,7	21	19	13	9,2	33
10	10	6,9	22	20	14	9,6	34

Задача 3 Нелинейная регрессия

Имеются данные по 10 хозяйствам

Урожайность, ц/га, y	15	18	17	22	25	20	24	19	23	27
Внесено удобрений, кг/га, x	2,1	3,6	3,5	5,0	6,5	4,2	6,3	4,0	6,0	7,5

Требуется:

1. Рассчитать параметры степенной и экспоненциальной парных регрессий.

2. Оценить тесноту связи с помощью показателей корреляции и детерминации.

3. Рассчитать средние коэффициенты эластичности и дать сравнительную оценку силы связи фактора с результатом.

4. С помощью F- критерия оценить статистическую надежность результатов моделирования.

5. Рассчитать линейный коэффициент корреляции и детерминации, сделать вывод о целесообразности замены нелинейной зависимости линейной.

6. На основании пунктов 3,4,5 выбрать наилучшее уравнение регрессии.

Решение.

1. Регрессия в виде степеннойфункции имеет вид.

Для оценки параметров линеаризуем модель путем логарифмирования:

,

Для расчетов составим таблицу:

Номер	x	y
1	2,1	15	0,7419	2,7081	2,0092	0,5505	4,41	5,6869
2	3,6	18	1,2809	2,8904	3,7024	1,6408	12,96	10,4053
3	3,5	17	1,2528	2,8332	3,5493	1,5694	12,25	9,9162
4	5,0	22	1,6094	3,0910	4,9748	2,5903	25	15,4552
5	6,5	25	1,8718	3,2189	6,0251	3,5036	42,25	20,9227
6	4,2	20	1,4351	2,9957	4,2991	2,0595	17,64	12,5821
7	6,3	24	1,8405	3,1781	5,8494	3,3876	39,69	20,0217
8	4,0	19	1,3863	2,9444	4,0819	1,9218	16	11,7778
9	6,0	23	1,7918	3,1355	5,6181	3,2104	36	18,8130
10	7,5	27	2,0149	3,2958	6,6408	4,0598	56,25	24,7188
	48,7	210	15,2255	30,2911	46,7501	24,4938	262,45	150,2997
Среднее значение	4,87	21	1,5225	3,0291	–	–	26,245	–

Таким образом, ,.

Уравнение регрессии .

Выполнив потенцирование, получим .

Параметр является коэффициентом эластичности и означает, что с ростом удобрений на 1% урожайность с гектара повышается на 0,48%.

Регрессия в виде экспоненциальнойфункции имеет вид .

Для оценки параметров линеаризуем модель путем логарифмирования:

,

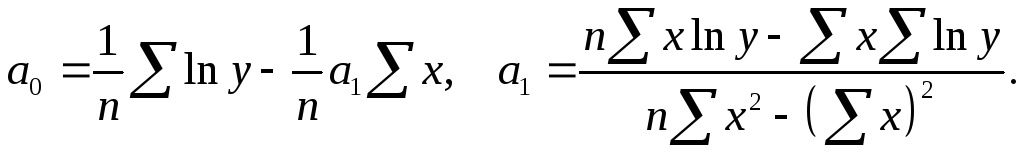
Расчетные данные приведены в таблице выше. Имеем:

,.

Уравнение регрессии .

Выполнив потенцирование, получим

2,3. Для расчета показателей корреляции и детерминации необходимо рассчитать теоретические значения по построенным моделям. Для этого подставим значения xв уравненияи, а результаты пропотенцируем.

Расчеты приведем в таблице. Индексы корреляции и детерминации будем рассчитывать по формулам ,.

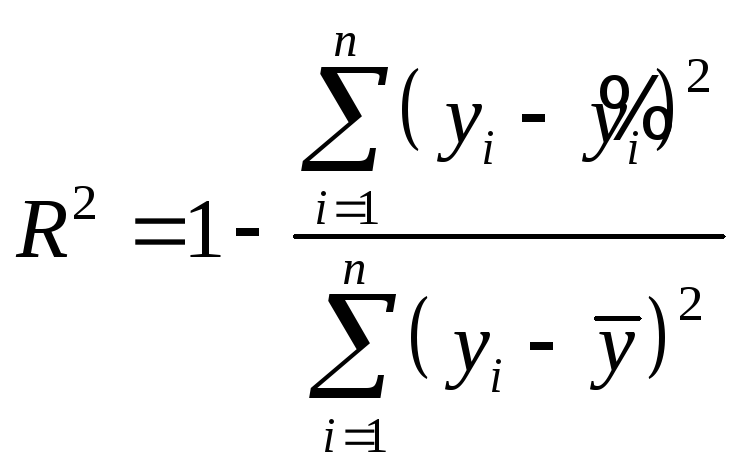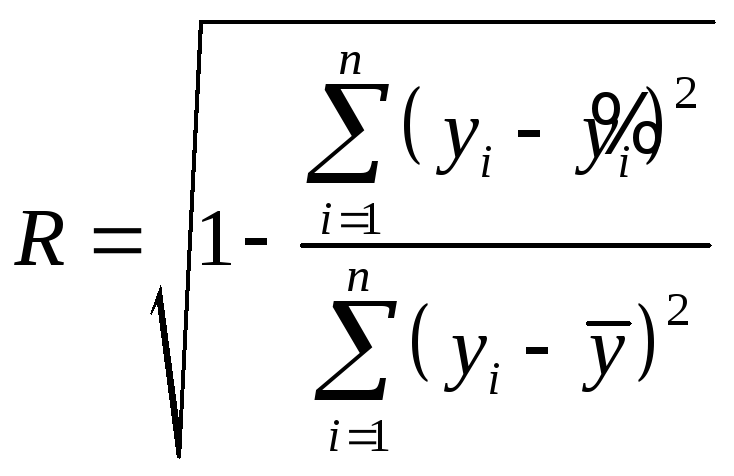Номер	y		Степенная функция			Экспоненциальная функция
1	15	36	2,6541	14,2126	0,6200	2,7244	15,2473	0,0611
2	18	9	2,9131	18,4131	0,1706	2,8894	17,9825	0,0003
3	17	16	2,8995	18,1656	1,3585	2,8784	17,7858	0,6175
4	22	1	3,0709	21,5607	0,1930	3,0434	20,9764	1,0477
5	25	16	3,1969	24,4569	0,2949	3,2084	24,7395	0,0679
6	20	1	2,9871	19,8284	0,0295	2,9554	19,2094	0,6250
7	24	9	3,1819	24,0925	0,0086	3,1864	24,2011	0,0405
8	19	4	2,9637	19,3690	0,1362	2,9334	18,7914	0,0435
9	23	4	3,1585	23,5344	0,2855	3,1534	23,4155	0,1727
10	27	36	3,2657	26,1974	0,6442	3,3184	27,6161	0,3796
	210	132	–	–	3,7410	–	–	3,0558

Для степеннойфункции индекс детерминации составит, а индекс корреляции. Таким образом, связь между рассматриваемыми признаками достаточно тесная. Величина индекса детерминации говорит о том, что 97 % изменчивости урожайности объясняется данным уравнением.

F-критерий Фишера составит :

.

Это значение превышает табличное значение на 5% уровне значимости , следовательно найденное уравнение регрессиистатистически значимо.

Для экспоненциальнойфункции индекс детерминации составит, индекс корреляции. Связь также является достаточно тесной, 98% изменчивости урожайности объясняется данным уравнением.

F-критерий Фишера составит :

.

Это значение превышает табличное значение на 5% уровне значимости , следовательно найденное уравнение регрессиистатистически значимо.

4.Индексы корреляции и детерминации рассчитанных моделей различаются незначительно. Возможно, является целесообразным заменить их более простой линейной моделью. Для этого рассчитаем парные линейные коэффициенты корреляции и детерминации по формулам:

,

где .

,,,

.

В случае экспоненциальной модели разность , следовательно, вместо экспоненциальной модели можно использовать линейную.

В случае степенной модели , что говорит о том, что применение более сложной формы зависимости только ухудшило качество модели.

5. Исходя из вышесказанного, делаем вывод о том, что оптимальной формой зависимости будет линейная, . Таким образом, при увеличении количества удобрений на 1 кг/га урожайность возрастает на 2,297 ц/га.

Имеются данные по 10 хозяйствам