Глава 6

ОСНОВНЫЕ ПОНЯТИЯ

И ОПРЕДЕЛЕНИЯ ТЕОРИИ

ИНФОРМАЦИИ

6.1. Мера количества информации

В теории информации изучаются количественные закономерности передачи, хранения и обработки информации.

Основное внимание в теории информации уделяется определению средней скорости передачи информации и решению задачи максимизации этой скорости путем применения соответствующего кодирования. Предельные соотношения теории информации позволяют оценить эффективность различных систем связи и установить условия согласования в информационном отношении источника с каналом и канала с потребителем.

Для исследования этих вопросов с общих позиций необходимо прежде всего установить универсальную количественную меру информации, не зависящую от конкретной физической природы передаваемых сообщений. Когда принимается сообщение о каком-либо событии, то наши знания о нем изменяются. Мы получаем при этом некоторую информацию об этом событии. Сообщение о хорошо известном нам собы­тии, очевидно, никакой информации не несет. Напротив, со­общение о малоизвестном событии несет много информации.

Таким образом, количество информации в сообщении о некотором событии существенно зависит от вероятпости этого события. Вероятностный подход и положен в основу определения меры количества информации. Для количественного определения информации, в принципе, можно использовать монотонно убывающую функцию вероятности F[P(a)], где P(a) – вероятность сообщения. Простейшей из них является функция 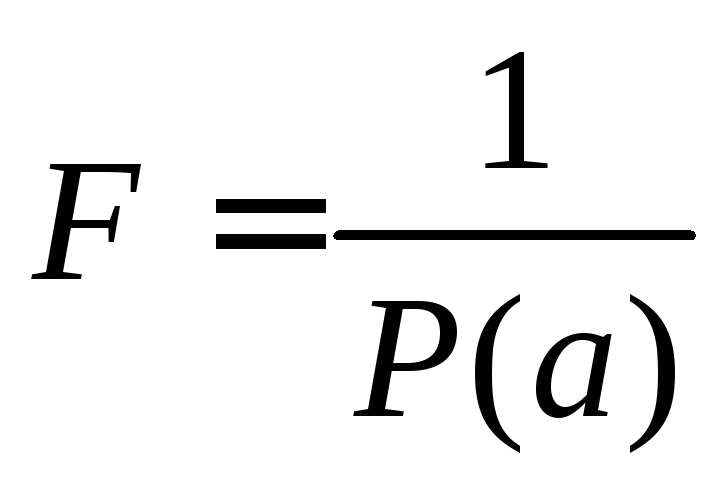, которая характеризует меру неожиданности (неопределенности) сообщения. Однако удобнее исчислять количество информации в логарифмических единицах, т. е. определять количество информации в отдельно взятом сообщении как:

(6.1)

Так как ,то J(a) – величина всегда положительная и конечная. При P(a)=1 количество информации равно нулю, т. е. сообщение об известном событии никакой информации не несет. Логарифмическая мера обладает естественным в данном случае свойством аддитивности, согласно которому количество информации, содержащееся в нескольких независимых сообщениях, равно сумме количества информации в каждом из них. Действительно, так как совместная вероятность n независимых сообщений , то количество информации в этих сообщениях равно:

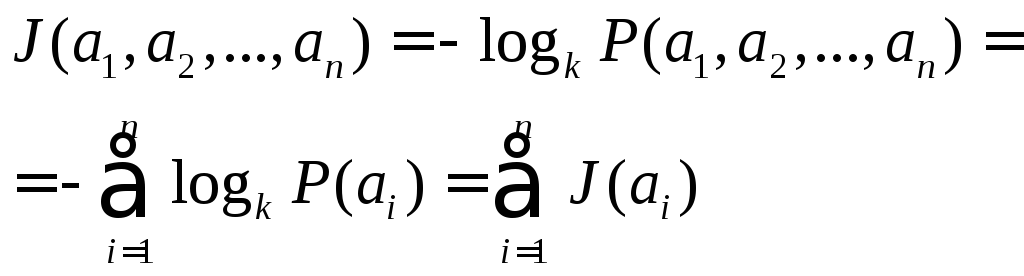(6.2)

что соответствует интуитивным представлениям об увеличении информации при получении дополнительных сообщений. Основание логарифма к может быть любым. Чаще всего принимают k=2, и тогда количество информации выражается в двоичных единицах:

дв. ед (6.3)

Двоичную единицу называют бит. Слово "бит" произошло от выражения binary digit (двоичная цифра). В двоичных системах передачи информации используется два символа, условно обозначаемых 0 и 1. В таких системах при независимых и равновероятных символах, когда P(0)=P(1)=1/2, каждый из них несёт одну двоичную единицу информации:

(6.4)

Формула (6.1) позволяет вычислять количество информации в сообщениях, вероятность которых отлична от нуля. Это, в свою очередь, предполагает, что сообщения дискретны, а их число ограниченно. В таком случае принято говорить об ансамбле сообщений, который описывается совокупностью возможных сообщений и их вероятностей:

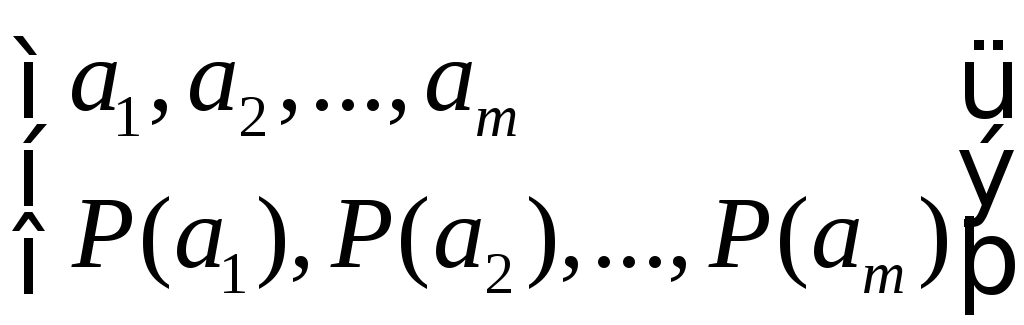(6.5)

Ансамбль сообщений образует полную группу событий, поэтому всегда:

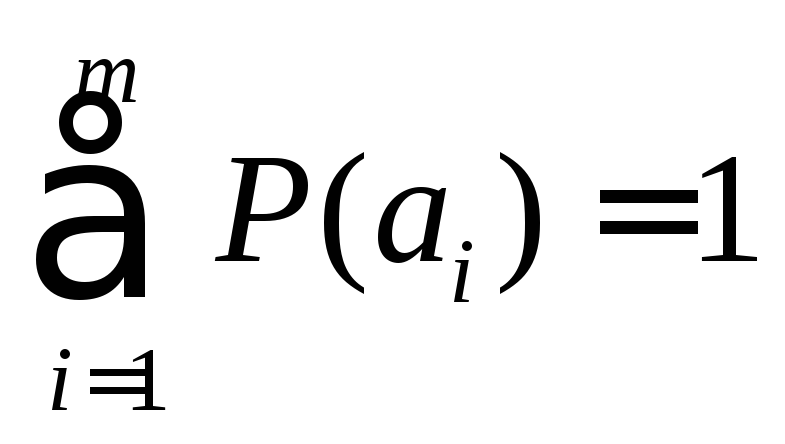
Если все сообщения равновероятны:

то количество информации в каждом из них определяется величиной:

(6.6)

Отсюда следует, что количество информации в сообщении зависит от ансамбля, из которого оно выбрано. До передачи сообщения имеется неопределенность относительно того, какое из т -сообщений ансамбля будет передано. После приема сообщения эта неопределенность снижается. Очевидно, чем больше т, тем больше неопределенностьи тем большее количество информации содержится в переданном сообщении.

Рассмотрим пример. Пусть ансамбль возможных сообщений представляет собой алфавит, состоящий из т различных букв. Необходимо определить, какое количество информации содержится в передаваемом слове длиной п букв, если вероятности появления букв одинаковы, а сами буквы следуют независимо друг от друга. Количество информации при передаче одной буквы:

Так как все буквы равновероятны, то и количество информации, содержащееся в любой букве, . Буквы следуют независимо, поэтому количетсво информации в слове изn букв:

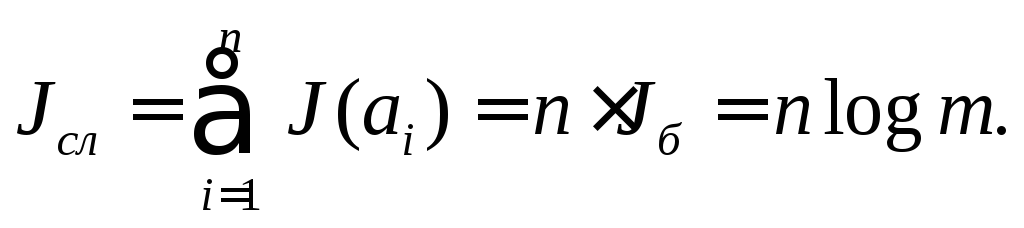(6.7)

К определению информации можно подойти и с другой стороны. Будем рассматривать в качестве сообщения не отдельную букву, а целое слово. Если все буквы равновероятны и следуют независимо, то все слова будут также равновероятны, и ,где -число возможных слов.Тогда можно записать: Для двоичного кода ансамбль элементарных сообщений состоит из двух элементов: 0 и 1(m=2). В этом случае сообщение и элементов несёт информацию:

(6.8)

В общем случае при передаче сообщений неопределенность снимается не полностью. Так, в канале с шумами возможны ошибки. По принятому сигналу v только с некоторой вероятностьюможно судить о том, что было передано сообщение a. Поэтому после получения сообщения остаётся некоторая неопределённость, характеризуемая величиной апостериорной вероятности , а количество информации, содержащееся в сигнале v, определяется степенью уменьшения неопределенности при его приеме. Если P(a) – априорная вероятность, то количество информации в принятом сигнале относительно переданного сообщения a, очевидно будет равно:

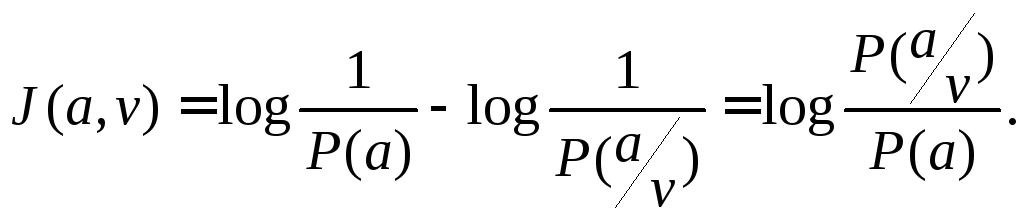(6.9)

Это выражение можно рассматривать также как разность между количеством информации, поступившим от источника сообщений, и тем количеством информации, которое потеряно в канале за счет действия шумов.