Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Краткий курс математического анализа. Том 2

.pdf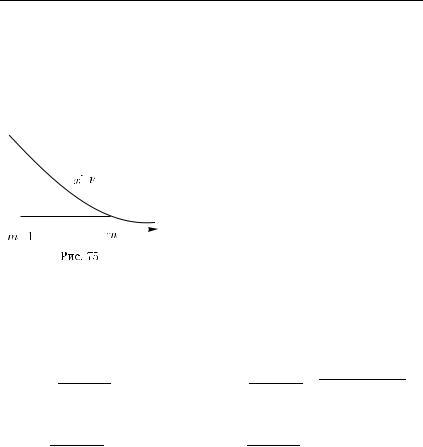

Скачиваний:

383

Добавлен:

10.05.2015

Размер:

4.49 Mб

Скачать

☆

<<< < Предыдущая 23 24 25 26 27 28 29 30 31 32 33 34 35 36 3738 / 4738 39 40 41 42 43 44 45 46 47 > Следующая >>>

370 Гл. 6. Гармонический анализ

Оценим остаток rn(x). При его оценке будет использовано неравенство Коши–Шварца для числовых рядов

∞ unvn					, un, vn R, n = 1, 2, ... (53.58)
		∞ un2		∞ vn2


n=1	n=1		n=1

(оно получатся предельным переходом из неравенства Коши–Шварца для конечных сумм) и неравенство

, p > 0,

(53.59)

m−1

которое

получается интегрированием

неравенства (рис. 75)

m1p

m − 1 x m,

Имеем

по отрезку [m − 1,

m].

∞

|rn(x)|

∞

εm

= m=n+1 am cos mx + bm sin mx

|am cos mx| + |bm sin mx| (53.44)

(53.58)

m=n+1

=n+1

2k =

εm

∞

m 1

−

(53.58)

m (53.59)

m=n+1

∞

2k 1

∞

−

+∞ dx

ηn

= 2

εm

2k 1

k 1/2

−

(53.60)

m=n+1

где

m=n+1

ηn =

∞

εm2 .

(53.61)

−

∞

εn2 (см. теорему 8) следует, что

Из сходимости ряда

n=1

∞

lim

ε2

= 0,

n→∞

а поэтому

=n+1

lim ηn

(53.62)

n→∞

(53.61)

§ 53. Ряды Фурье в гильбертовых пространствах

371

Из (53.60) и (53.62) в силу равенства (53.57) следует утверждение (53.53). Элементы последовательности ηn не зависят от x, поэтому из неравенства (53.53) и выполнения условия (53.62) следует, согласно признаку Вейерштрасса, равномерная сходимость ряда Фурье функции f.

Наконец, цепочка неравенств (53.60) содержит в себе неравенство

∞	(53.60) ηnn−k+1/2,
\|am cos mx\| + \|bm sin mx\|	(53.60) ηnn−k+1/2,	(53.63)
=n+1	(53.61)
m	(53.61)

из которого следует, что остатки ряда, составленного из абсолютных величин членов ряда (53.55), стремятся к нулю, а поэтому ряд (53.55) абсолютно сходится.

53.6. Ряды Фурье функций с произвольным периодом.

Теория ряда Фурье 2π-периодических функций переносится на функции с произвольным периодом 2l, l > 0. Для этого достаточно линейно отобразить отрезок [−l, l] на отрезок [−π, π]:

y =	π	x, −l x l, −π y π,	(53.64)
	l

и тогда вопрос об определении ряда Фурье для 2l-периодической функции сведется к вопросу о ряде Фурье 2π-периодической функции в следующем смысле. Если функция f (x) имеет период 2l и абсолютно интегрируема на периоде, т. е. абсолютно интегрируема на отрезке [−l, l], то после замены переменного x = πl y, обратной к отображению (53.64), получится 2π-периодическая абсолютно интегрируемая

на периоде функция f			l	y . Выполнив в ее ряде Фурье замену пере-
на периоде функция f			π	y . Выполнив в ее ряде Фурье замену пере-
менного (53.64), т. е.	вернувшись к исходной переменной, получим ряд
менного (53.64), т. е.
			∞
					nπx		nπx
a0 +				an cos		+ bn sin		,	(53.65)
					l		l
		n=1

называемый рядом Фурье заданной 2l-периодической функции f (x). Формулы для коэффициентов ряда (53.65) с помощью той же

замены переменного (53.64) следуют из формул для коэффициентов Фурье 2π-периодической функции:

f (x) dx, an =

f (x) cos

nπx

dx,

−l

bn =

f (x) sin

nπx

dx,

n = 1, 2, ... .

−l

372	Гл. 6. Гармонический анализ

С помощью замены переменного (53.64) доказанные выше теоремы для рядов Фурье 2π-периодических функций переносятся на ряды Фурье 2l-периодических функций.

53.7. Запись рядов Фурье в комплексной форме. Если функция f абсолютно интегрируема на отрезке [−π, π] и

∞

f a0 +

an cos nx + bn sin nx,

(53.66)

n=1

то, представив cos nx и sin nx по формулам Эйлера:

cos nx =

einx + e−inx

sin nx =

einx − e−inx

и сделав подстановку в ряд (53.66), получим

a +

∞ a

einx + e−inx

einx − e−inx

−

∞

n=1

= a0 +

(an − ibn)einx + (an + ibn)e−inx.

n=1

Если ввести обозначения

= a

, c

an − ibn

−

an + ibn

, n = 1, 2, ...,

(53.67)

то получим запись ряда Фурье в комплексной форме

+∞

cneinx,

n=−∞

где для коэффициентов cn имеют место формулы

f (x) dx,

2π

−π

an − ibn

f (x)(cos nx

−

i sin nx) dx =

f (x)e−inx

2π

−π

c−n =

+ ib

f (x)(cos nx + i sin nx) dx =

f (x)einx

2π

−π

n = 1, 2, ... .

−π

Объединив получившиеся формулы в одну, получим

dx,

	1	π
cn =		f (x)e−inx dx, n = 0, ±1, ±2, ... .
	2π

−π

Очевидно, что из формул (53.67) следует, что коэффициенты cn и c−n являются сопряженными комплексными числами: c−n = cn.

§ 54. Интеграл Фурье и преобразование Фурье

373

§ 54. Интеграл Фурье и преобразование Фурье

54.1. Представление функций интегралом Фурье. Пусть функция f задана на всей числовой прямой R и абсолютно интегрируема на ней. Сопоставим функции f интеграл

			+∞
			[a(y)cos xy + b(y)sin xy] dy,			(54.1)
где			0
где
a(y) =	1	+∞		1	+∞
	1		f (t) cos yt dt, b(y) =	1	f (t) sin yt dt.	(54.2)
	π		f (t) cos yt dt, b(y) =	π	f (t) sin yt dt.	(54.2)
	π			π	−∞
		−∞			−∞

Интеграл (54.1) аналогичен ряду Фурье периодической функции: суммирование заменено интегрированием. Функции a(y) и b(y) в подынтегральном выражении аналогичны коэффициентам Фурье.

Подставив (54.2) в подынтегральное выражение интеграла (54.1), будем иметь

1	+∞	+∞
1	dy	f (t)(cos xy cos yt + sin xy sin yt) dt =

π
π		−∞					+∞	+∞
	0	−∞				1	+∞	+∞
					=	1		dy f (t) cos y(x − t) dt.	(54.3)
					=	π		dy f (t) cos y(x − t) dt.	(54.3)
					0			−∞
	О п р е д е л е н и е 1. Интеграл
		1		+∞	+∞
		1			dy f (t) cos y(x − t) dt				(54.4)

			π
		0			−∞

называется интегралом Фурье функции f.

Подобно тому, как при определенных условиях периодическая функция раскладывается в ряд Фурье, функция, определенная на всей числовой оси, представляется своим интегралом Фурье. Прежде чем это доказывать, докажем одно вспомогательное утверждение.

Л е м м а 1. Если функция f (x) абсолютно интегрируема на всей числовой оси, а функция ϕ(x, y) непрерывна и ограничена в полосе

Π = {(x, y) : −∞ < x < +∞, −∞ < c y d < +∞},		(54.5)
то:
1) функция	+∞
	+∞
	def	(54.6)
	Φ(y) = f (x)ϕ(x, y) dx	(54.6)

−∞

непрерывна на отрезке [c, d];

374 Гл. 6. Гармонический анализ

2) справедливо равенство

d	d	+∞	+∞	d
Φ(y) dy =	dy	f (x)ϕ(x, y) dx =	f (x) dx	ϕ(x, y) dy. (54.7)
c	c	−∞	−∞	c

В силу ограниченности функции ϕ(x, y) в полосе Π (см. (54.5)) существует такая постоянная M > 0, что для всех точек (x, y) Π выполняется неравенство

\|ϕ(x, y)\| M	(54.8)
и, следовательно,
\|f (x)ϕ(x, y)\| M \|f (x)\|.	(54.9)

Согласно условию леммы функция f (x) абсолютно интегрируема на всей числовой оси, поэтому по признаку Вейерштрасса интеграл (54.6) так же, как и интеграл

+∞

|f (x)ϕ(x, y)| dx,

(54.10)

−∞

равномерно сходятся на отрезке [c, d]. Следовательно, функция Φ(y) определена на отрезке [c, d]. Докажем ее непрерывность.

Из плотности непрерывных финитных функций в пространстве RL(−∞, +∞) абсолютно интегрируемых функций (см. теорему 7 в п. 53.8) и абсолютной интегрируемости функции f на числовой оси следует существование таких непрерывных финитных функций fn, что

supp fn [αn, βn],	−∞ < αn < βn < +∞, n = 1, 2, ...,
+∞
nlim	\|f (x) − fn(x)\| dx = 0.	(54.11)
→∞

−∞

Положим

+∞	βn
Φn(y) =	fn(x)ϕ(x, y) dx = fn(x)ϕ(x, y) dx,	(54.12)
−∞		(54.12)
−∞	αn
	c y d, n = 1, 2, ... .

Функция Φn(y) непрерывна на отрезке [c, d], так как подынтегральная функция fn(x) ϕ(x, y) непрерывна на конечном прямоугольнике {(x, y) : αn x βn, c y d} (см. теорему 2 в п. 49.2)

§ 54. Интеграл Фурье и преобразование Фурье

375

Для любой точки y [c, d] выполняется неравенство

+∞

\|	−	Φn(y)	\|	(54.6)	\|	−	\|\|	\|		\|
Φ(y)		Φn(y)			f (x)		fn(x) ϕ(x, y)		dx
				(54.12) −∞				+
							M	∞
							M	\|f (x) − fn(x)\| dx. (54.13)

−∞

В правой части неравенства (54.13), в силу выполнения условия (54.11), стоит бесконечно малая числовая последовательность. Отсюда следует, что последовательность непрерывных на отрезке [c, d] функций Φn(y), n = 1, 2, ..., сходится и притом равномерно на этом отрезке к функции Φ(y) (см. следствие из леммы 1 в п. 31.2):

Φn(y) Φ(y), n → ∞.

[c,d]

Поэтому функция Φ(y) непрерывна на отрезке [c, d] (см. теорему 7 в п. 31.4).

Докажем теперь формулу (54.7). Прежде всего заметим, что в силу доказанной непрерывности функции (54.6) интеграл в левой части равенства (54.7) существует как интеграл от функции Φ(y) по отрезку, на котором она непрерывна. Существование интеграла в правой части равенства (54.7) следует из того, что функция

def ,

Ψ(x) = f (x) ϕ(x y) dy

является произведением абсолютно интегрируемой на числовой оси R

функции f (x) на ограниченную непрерывную функцию ϕ(x, y) dy

(см. замечание в п. 29.5). Здесь непрерывность собственного интегра-

ла ϕ(x, y) dy по параметру x на любом конечном отрезке, а поэтому

и на всей числовой оси следует из теоремы 2 п. 49.2, а его ограниченность — из ограниченности функции ϕ:

d	ϕ(x, y) dy	d \|ϕ(x, y)\| dy M (d − c).

		(54.8)

Далее, в силу теоремы 7 из п. 52.7 для произвольного ε > 0 существует такая непрерывная финитная функция fε, что

+∞

|fε(x) − f (x)| dx < ε.

(54.14)

−∞

376 Гл. 6. Гармонический анализ

Для этой функции fε, согласно теореме 4 п. 49.2, справедлива формула

d	+∞	+∞	d
dy	fε(x)ϕ(x, y) dx =		fε(x) dx ϕ(x, y) dy	(54.15)
c	−∞	−∞	c

(здесь в силу финитности функции fε можно бесконечные пределы заменить конечными, поэтому здесь и применима теорема 4 из п. 49.2). Покажем, что предел левой части равенства (54.13) при ε → 0 равен

d	+∞	+∞	d
dy	f (x)ϕ(x, y) dx, а правой —	f (x) dx	ϕ(x, y) dy. Для этого
c	−∞	−∞	c

оценим отклонения левой и правой частей равенства (54.15) от их предполагаемых предельных значений. Имеем

+∞

−∞

dy fε(x)ϕ(x, y) dx

− c

dy f (x)ϕ(x, y) dx

+∞

fε(x)

−

| |

∞

−

dx =

(54.8)

f (x) ϕ(x, y)

M dy

fε(x)

f (x)

−∞

+∞

−∞

= M (d

−

|fε(x) − f (x)| dx

< M (d

−

c)ε. (54.16)

(54.14)

−∞

Соответственно для правой части

+∞

−∞

+∞

−∞

fε(x) dx c ϕ(x, y) dy

− f (x) dx c ϕ(x, y) dy

−

(54.8)

fε(x)

f (x)

dx ϕ(x, y)

−∞

+∞

fε(x)

−

f (x)

dx dy M (d

−

c)ε. (54.17)

(54.8)

−∞

(54.14)

Положив в равенстве (54.15) ε → 0, получим в силу (54.16) и (54.17) равенство (54.7).

Те о р е м а 1. Если функция f абсолютно интегрируема на всей числовой оси R, то в каждой точке x R, в которой существуют

§ 54. Интеграл Фурье и преобразование Фурье

377

f+(x) и f−(x), имеет место равенство

f (x + 0) + f (x − 0)		1	+∞	+∞
	=			dy f (t) cos y(x	−	t) dt.	(54.18)
		π
2				−∞
		0

Зафиксируем произвольно точку x R, в которой существуют f+(x) и f−(x) (а следовательно, существуют и f (x + 0), f (x − 0)), и положим

	η	+∞
def 1		+∞
def 1		f (t) cos y(x − t) dt, η > 0.
S(η) = π	dy	f (t) cos y(x − t) dt, η > 0.	(54.19)
	0	−∞

Функция S(η) является для интеграла Фурье аналогом частичной суммы ряда Фурье периодической функции.

Поскольку функция cos y(x − t) непрерывна и ограничена на всей плоскости переменных y и t, то согласно формуле (54.7) в интеграле (54.19) можно поменять порядок интегрирования. Проделав это, получим

+∞ η

S(η) =

f (t) dt cos y(x − t) dy

(54.19) π

(54.7)

−∞

+∞

sin η(x − t)

f (t)

−∞

x − t

u=t−x

f (x + u)

sin ηu

du +

1	+∞
	f (x + u)	sin ηu	du =
π
		u
	−∞

+∞

f (x + u) sin ηu du = u

−∞	0
	+∞

=	1	[f (x + t) + f (x − t)]	sin ηt	dt. (54.20)
=	π	[f (x + t) + f (x − t)]	t	dt. (54.20)
		0

Формула (54.20) по своему виду напоминает соответствующую формулу для частных сумм ряда Фурье (см. формулу (51.40)). Поэтому естественно провести дальнейшие рассуждения по той же схеме, которая применялась в рядах Фурье при доказательстве формулы (51.51), учитывая, конечно, специфику рассматриваемого случая.

Вспомнив, что (см. п. 50.4)

+∞

sin ηt	dt =	π		(54.21)
			, η > 0,
t		2

378 Гл. 6. Гармонический анализ

преобразуем разность между S(η)

f (x + 0) + f (x − 0)

следующим

образом:

S(η)

f (x + 0) + f (x − 0)

+∞

sin ηt

−

[f (x + t) + f (x

−

t)]

−

(54.20)

(54.21)

+∞

f (x + 0) + f (x − 0)

sin ηt

dt =

(54.22)

−

+∞

sin ηt

+∞

sin ηt

[f (x + t) − f (x + 0)]

dt +

[f (x − t)

− f (x − 0)]

dt.

Получившиеся интегралы представим в виде сумм интегралов по промежуткам [0, 1] и [1, +∞]:

+∞	1	+∞
=	+	(54.23)
0	0	1

и исследуем каждый из получившихся интегралов отдельно.

Так как в силу условий теоремы существует конечный предел

lim f (x + t) −t f (x + 0) = f+(x),

t→0

и так как функция f (x + t) − f (x + 0) абсолютно интегрируема по переменному t на отрезке [0, 1] (напомним, что x фиксировано),

то и функция

f (x + t) − f (x + 0)

абсолютно интегрируема на этом

отрезке. Поэтому по теореме Римана (п. 51.3, теорема 3)

f (x + t) − f (x + 0)

lim

sin ηt dt = 0.

(54.24)

η→+∞

Для соответствующего интеграла по промежутку [1, +∞) имеем

+∞

sin ηt

[f (x + t) − f (x + 0)]

+∞

f (x + t)

sin ηt dt −

f (x + 0)

sin ηt

dt.

(54.25)

Поскольку при t 1 выполняется неравенство

|f (x + t)|

f (x + t) ,

§ 54. Интеграл Фурье и преобразование Фурье

379

то в силу абсолютной интегрируемости функции f на всей числовой оси будем иметь

+∞

|f (x + t)|

f (x + t)

dt =

u=x+t

−∞

+∞

du < +

∞

u=x+t

f (u)

−∞

т. е. функция

f (x + t)

абсолютно

интегрируема

на

промежутке

[1, +∞), и поэтому снова по теореме Римана получим

lim

+∞

f (x + t)

sin ηt dt = 0.

(54.26)

η→+∞ π

+∞

Наконец, из сходимости интеграла

sin x dx следует, что

f (x + 0)

+∞

f (x + 0)

+∞

lim

sin ηt

lim

sin u

du = 0.

(54.27)

η→+∞

ηt=u

η→+∞

В результате из полученных равенств (54.24)–(54.27) вытекает, что

+∞

f (x + 0)] sin ηt dt = 0.

lim

[f (x + t)

−

(54.28)

→ ∞

Аналогично доказывается, что

lim

+∞

sin ηt

[f (x − t)

− f (x −

54 29

η +

)]

dt = .

( . )

→ ∞

Таким образом, для интеграла Фурье (54.3) функции f имеем

+∞	+∞				S(η) = f (x + 0) + f (x − 0) .
dy	f (t) cos y(x	−	t) dt =	lim	S(η) = f (x + 0) + f (x − 0) .
			(54.19) η	→ ∞	2
			(54.19) η	+	2

0−∞

Пр и м е р. Представим интегралом Фурье функцию

1,	если	x 1,
f (x) = 0,	если	\|\|x\|\| > 1.

<<< < Предыдущая 23 24 25 26 27 28 29 30 31 32 33 34 35 36 3738 / 4738 39 40 41 42 43 44 45 46 47 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.09.2019317.95 Кб17Копия Т Ф К П.doc
#
10.05.20151.13 Mб11КР по ТПР Чекменёв А.С..docx
#
10.05.2015649.22 Кб91КР_Ромашин_РС110_2012_1.doc
#
24.09.2019131.07 Кб7КРАТКАЯ ХАРАКТЕРИСТИКА ОСНОВНЫХ АХОВ.doc
#
10.05.20155.57 Mб813Краткий курс математического анализа. Том 1.pdf
#
10.05.20154.49 Mб383Краткий курс математического анализа. Том 2.pdf
#
22.12.2019144.9 Кб0Кратко 31-40.doc
#
10.05.20151.56 Mб92краткое сожержание курса БЖД.doc
#
16.11.201929.92 Кб34кризис.docx
#
16.03.20162.51 Mб740Криминология Малков В. Д..doc
#
27.11.2019524.29 Кб78Курс лекций Интернет-технологии.doc