
- •5. Мониторинг процесса выполнения курсового проекта (работы)
- •Оглавление
- •Задание 1 Теоретическая часть
- •Условия задания
- •Исходные данные
- •Расчетная часть
- •I.Сигнал
- •II. Переменная составляющая
- •Условия задания
- •Исходные данные
- •Расчетная часть
- •Задание 3 Теоретическая часть
- •Условия задачи
- •Расчетная часть
- •Задание 4
- •Теоретическая часть
- •Условия задания
- •Исходные данные
- •Расчетная часть
- •Задание 5. Теоретическая часть
- •Условия задания
- •Исходные данные
- •Расчетная часть
Условия задания
На входы амплитудно-импульсного модулятора (АИМ) поданы:
1.) несущее колебание в виде периодической последовательности однополярных прямоугольных импульсов со следующими параметрами:
амплитуда импульсов

 =
(N1+2) В,
=
(N1+2) В,частота сигнала F= (N1 +N2 + 1)·103Гц,
длительность импульса tи=
 ,
где Т – период последовательности
импульсов.
,
где Т – период последовательности
импульсов.
2.) модулирующий сигнал: e(t) = (N2+2)·Cos(2Ωt) + (N1+1)·Cos(3Ωt), где Ω = πF/6.
Выберите глубину модуляции импульсов М такой, чтобы передаваемая информация не искажалась.
Приведите аналитическое выражение и изобразите временную диаграмму для сигнала на выходе модулятора.
Рассчитайте параметры спектра и постройте спектральную диаграмму сигнала на выходе модулятора.
Исходные данные
1) несущее колебание
 Um
=4В
Um
=4В
 F=8*10-3 Гц
F=8*10-3 Гц
 tu
=1/48 = 0.0208 *10-3 c=
20.8 *10-6 c
tu
=1/48 = 0.0208 *10-3 c=
20.8 *10-6 c
 T=
1/8 мс = 0.125 *10-3с=125 *10-6с
T=
1/8 мс = 0.125 *10-3с=125 *10-6с


Несущее колебание
2) модулирующий сигнал:
Ω= πF/6 =4118.39 рад/с
e(t) = 5*Cos (8234.78*t) + 6*Cos (12354.25*t)

Модулирующее колебание
Расчетная часть
Выбор глубины модуляции
Искажение сигнала возникает из-за перемодуляции сигнала.
Методом построения результирующего сигнала определяем допустимую глубину модуляции: М=10%
Сигнал на выходе модулятора
Уравнение модулированного сигнала:
UUM(t)
= 1+M* [Bm*cos(2Ωt) +Em
* cos(3Ωt)])
* (Ao
+∑nk=1
Amk
cos(k* ω
*t), где : 
Ao=Um/Q
 Amk
= (2Um/Q)*
[sin((kωtu)/2))/
((kωtu)/2))]
Amk
= (2Um/Q)*
[sin((kωtu)/2))/
((kωtu)/2))]
 Q= T/tu
Q= T/tu
 ω = 2п
ω = 2п
M-глубина модуляции в долях.
Подставим исходные данные:

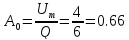


Тогда, уравнение модулированного сигнала приобретёт вид:


Вид сигнала для К=10 в масштабе времени как и на графике с изображением модулирующего сигнала.


Промодулированный сигнал
Для построение спектра сигнала раскроем скобки в уравнении модулированного сигнала и посмотрим какие составляющие будут у спектра:
 В выражении
приведённом выше использовалось правило
произведения косинусов:
В выражении
приведённом выше использовалось правило
произведения косинусов:

Видно, что спектр будет иметь тот же вид, что и спектр АИМ с однотональной модуляцией, но будет иметь дополнительные боковые составляющие в каждом интервале.
Подставим исходные данные:

Graph.png
Спектральное представление сигнала
Задание 3 Теоретическая часть
В теории спектрального анализа непериодических сигналов используется искусственный прием: одиночный импульс заменяется периодической последовательностью с бесконечно большим периодом следования.
Тогда сигнал запишется как:

В этом случае выражение рядов Фурье для периодического сигнала сохраняет смысл и приобретает вид:

Поскольку Т=2π/ω, то формула перепишется:

В предельном
случае, когда T
 и спектр сигнала станет не дискретным,
а сплошным, а амплитуды отдельных
составляющих будут стремиться к нулю.
и спектр сигнала станет не дискретным,
а сплошным, а амплитуды отдельных
составляющих будут стремиться к нулю.
При этом
 и переходит вdw,
и переходит вdw,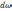 ,
аnω превращается в текущую
частоту ω.
,
аnω превращается в текущую
частоту ω.
Тогда Сумма в последнем выражении превращается в интеграл:


Отсюда получим:

S(ω) -спектральная плотность сигнала
И соответственно:

Эти два выражения носят названия прямого и обратного преобразования Фурье.
Они связывают
вещественную функцию
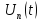 (сигнал) и комплексную функцию частоты
(сигнал) и комплексную функцию частоты (спектральная плотность сигнала)
(спектральная плотность сигнала)
S(ω) характеризует интенсивность сплошного распределения амплитуд гармоник непериодического сигнала вдоль оси частот.
