Практические работы по МММ_ 1-2_16_10_2014

Практические работы по предмету

"Методы математического моделирования"

Практическая работа №1

Расчёт распределения примеси при ионной имплантации

1. Цель работы.

Провести расчёт профилей распределения различных типов примеси в результате проведения процесса ионной имплантации с помощью двух математических моделей.

2. Общие положения

Ионная имплантация – процесс внедрения в мишень ионизированных атомов с энергией, достаточной для проникновения в ее приповерхностные области. На рис. 1 представлено схематическое изображение процесса, а также профиль распределения имплантированной примеси.

Рис. 1 Схематическое изображение процесса ионной имплантации и профиль распределения примеси в результате её проведения

При анализе профиля распределения примеси, полученного с помощью процесса ионной имплантации, используются следующие термины и определения:

- общая длина траектории движения иона – длина пробега (R);

- расстояние, проходимое ионом до остановки в направлении, нормальном к поверхности мишени – проецированная длина пробега (R_p);

- случайный разброс проецированной длины пробега (DR_p);

- среднеквадратичное отклонение (DR_p²);

- доза имплантации (число имплантированных атомов на единицу площади см^-2) – Q.

Первым математическим описание распределения внедренных ионов по глубине является описание с помощью симметричной функции распределения Гаусса (1):

(1)

Максимальная концентрация на глубине проецируемой длины пробега n(R_p) определяется соотношением (2):

(2)

Таблица 1 Параметры имплантированных ионов бора, алюминия, фосфора, мышьяка и сурьмы для распределения Гаусса

E (кэВ)			B		Al		P		As		Sb
20	Rp (нм)	78		29		26		16		14
	ΔRp (нм)	32		11		9,4		3,7		2,4
40	Rp (нм)	161		56		49		27		23
	ΔRp (нм)	54		19		16,4		6,2		3,8
60	Rp (нм)	244		85		73		38		31
	ΔRp (нм)	71		27		23		8,4		5,1
80	Rp (нм)	324		114		98		48		38
	ΔRp (нм)	84		35		30		10,5		6,3
100	Rp (нм)	398		144		123		58		46
	ΔRp (нм)	94		42		35		12,5		7,4
120	Rp (нм)	469		175		149		68		53
	ΔRp (нм)	102		48		41		14,5		8,4
140	Rp (нм)	537		205		175		79		60
	ΔRp (нм)	110		54		47		16		9,5
160	Rp (нм)	603		236		201		89		67
	ΔRp (нм)	116		60		52		18		10,5
180	Rp (нм)	665		266		228		99		74
	ΔRp (нм)	121		60		57		20		11,5
200	Rp (нм)	725		297		254		110		81
	ΔRp (нм)	126		70		61		22		12,5

Недостатком описания с помощью функции Гаусса является отсутствие учета зависимости пробега внедренных ионов от различных факторов в многослойные мишени и эффекты каналирования.

Усовершенствование модели является использование функции распределения ионов, имеющей вид сдвоенной полугауссианы - гауссианы с различными значениями дисперсии на левом и правом плечах распределения. Функция распределения примеси имеет вид согласно выражению (3), а общее распределение примеси рассчитывается согласно выражению (4):

(3)

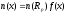(4)

Представленный тип распределения примеси удовлетворительно описывает распределения фосфора, мышьяка и сурьмы. Основные параметры для данного распределения представлены в таблице 2.

Таблица 2 Параметры имплантированных ионов фосфора, мышьяка и сурьмы для сдвоенного распределения Гаусса

	E (кэВ)	20	40	60	80	100	200	400	600	800	1000
Rp (нм)	P	21,8	44,34	68,94	94,95	122	263,6	545,7	810	1060	1295
	As	19,0	31,60	44,32	35,25	72,8	134,7	253,2	344,7	484,6	609,2
	Sb	12,36	20,67	27,84	–	41,45	174,1	140,5	210,7	284,3	360,3
σ1 (нм)	P	7,343	15,66	24,7	34	43,35	87,54	161	220	270	316,5
	As	9,11	14,44	19,864	25,484	31,50	55,08	86,96	96,55	133,5	157,3
	Sb	2,07	4,21	5,622	–	8,53	15,55	29,83	45,33	61,43	77,53
σ2 (нм)	P	15,6	25,8	34,35	41,63	47,8	68,97	81,39	50	13,5	15,6
	As	7,957	13,04	17,17	20,17	22,55	39,16	81,36	136,7	161,3	192,6
	Sb	5,925	9,543	12,78	–	18,65	31,83	55,85	77,25	96,84	115

Для совершенствования расчёта распределения имплантированной примеси может быть использовано распределение Пирсона. Распределение Пирсона учитывает четыре параметра процесса имплантации: R_p, DR_p, несимметричность g и затухание b. В общем виде распределение Пирсона определяется дифференциальным уравнением (5):

(5)

Постоянные в распределении Пирсона могут быть выражены с помощью следующих соотношений (6) – (10) и рассчитываются на основе параметров процесса имплантации (11) – (14):

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

Основные параметры распределения бора приведены в таблице 3.

Таблица 3 Параметры имплантированных ионов бора для распределения Пирсона

E (кэВ)	10	30	50	70	100	200	300	400	600	800
Rp (нм)	40	101,5	164,5	226	310	556	735,5	900	1237,5	1515
ΔRp (нм)	28	42,5	57	70	84,5	110	116	127	130	146,5
γ	–0,3	–0,55	–1,0	–1,0	–1,3	–2,15	–2,25	–2,75	–2,6	–3,3
β	2,9	3,6	5,5	5,5	7,5	17,5	19	32	28	60

Таким образом, функция распределения Пирсона определяется следующим соотношением (15):

(15 )

Общее распределение примеси как и ранее определяется соотношением (4).

3. Задания для работы

В результате выполнения работы необходимо:

а) Провести расчёт распределений примеси по глубине с использованием распределения распределение Гаусса или. Варианты задания приведены в таблице 4.

Таблица 4 Задание для расчета имплантации с помощью распределения Гаусса

Вариант	Примесь	Энергия (кэВ)	Доза (мкКл/см2)
1	B	80	5
2	Al	20	50
3	As	20	25
4	B	140	50
5	P	100	100
6	Sb	200	500
7	Sb	160	25
8	As	100	50
9	B	60	50
10	As	60	100
11	B	200	1000
12	Sb	80	5
13	As	200	1000
14	B	180	25
15	P	20	5
16	As	80	25
17	B	200	200
18	Al	70	5
19	B	20	300
20	P	60	500

б) Провести расчёт распределений примеси по глубине с использованием сдвоенного распределения Гаусса. Варианты задания приведены в таблице 5.

Таблица 5 Задание для расчета имплантации с помощью сдвоенного распределения Гаусса

Вариант	Примесь	Энергия (кэВ)	Доза (мкКл/см2)
1	As	20	5
2	Sb	40	25
3	P	600	50
4	P	80	100
5	Sb	100	500
6	P	400	100
7	Sb	80	50
8	As	1000	25
9	P	40	50
10	As	800	100
11	P	60	5
12	Sb	1000	1000
13	P	200	25
14	As	20	50
15	Sb	60	5
16	As	80	5
17	P	100	1000
18	Sb	40	25
19	P	800	50
20	Sb	60	5

в) Оформить результаты измерения.

Учебная литература:

1. Технология СБИС: В 2-х кн. Кн.1 Пер. с англ. /Под ред. С. Зи. – М.: Мир, 1986. – 404 с., ил.

2. Моделирование интегральных микротехнологий, приборов и схем: Учеб. пособие для спец. "Физика и технология материалов и компонентов электронной техники". – М.: Высш. шк., 1989. – 320 с.:ил.

Практическая работа №2

Расчёт распределения примеси при диффузии

1. Цель работы.

Провести расчёт коэффициента диффузии в зависимости от температуры, профилей распределения различных типов примеси в результате проведения процесса диффузии из бесконечного и ограниченного источников.

2. Общие положения

Диффузией называется перенос атомов вещества, обусловленный их хаотическим тепловым движением, в направлении уменьшения концентрации. Основные механизмы диффузии представлены на рис. 1.

Рис. 1 Основные механизмы диффузии примеси

В диапазоне температур коэффициент диффузии обычно описывается уравнением Аррениуса (1):

(1)

где E_A – энергия активации; k – постоянная Больцмана; T – температура.

Данная модель предполагает взаимодействие примеси при диффузии только с одним каким-либо видом дефектов, находящимся в состоянии равновесия. Параметры, используемые в уравнении (1) для различных типов примеси приведены в таблице 1.

Таблица 1 Параметры уравнения Аррениуса

Элемент	D0 (см2/с)	EA (эВ)
B	10,5	3,69
Al	8,0	3,47
Ga	3,6	3,51
In	16,5	3,90
P	10,5	3,69
As	0,32	3,56
Sb	5,60	3,95

Для анализа процесса диффузии используется два закона Фика.

Первый закон Фика (2):

(2)

где j – плотность потока атомов; D – коэффициент диффузии; N – концентрация атомов.

Второй закон Фика 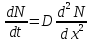(3):

(3)

Диффузия обычно проводится в два этапа: загонка и разгонка.

Двум этапам диффузионного процесса соответствует два решения уравнения Фика при различных граничных условиях:

- первый этап – диффузия с постоянной поверхностной концентрацией или диффузия из бесконечного источника;

- второй этап – диффузия из ограниченного источника.

Цель первого этапа – внедрение в полупроводник точно контролируемого количества примеси. Решение уравнений Фика для данного этапа диффузии определяется соотношением (4). Общее количество примеси, поступившее в полупроводник определяется соотношением (5).

(4)

(5)

Предел растворимости примеси в кремнии, определяющий максимальное значение концентрации N₀, для различных температур (сплошная линия) представлен на рис. 2.

Рис. 2 Зависимость предела твердой растворимости в кремнии в диапазоне температур

Цель второго этапа – получение заданного распределения примеси. Решением уравнения Фика для данного этапа является соотношение (6):

(6)

3. Задания для работы

а) Построить зависимость коэффициента диффузии от температуры

Вариант	Примесь
1	B
2	Sb
3	P
4	As
5	Sb
6	As
7	B
8	Sb
9	B
10	As
11	P
12	Sb
13	P
14	B
15	Sb
16	As
17	P
18	B
19	Sb
20	B