Метод Ньютона

Этот метод обладает гораздо более быстрой сходимостью, чем метод простой итерации и метод Зейделя. В случае одного уравнения алгоритм метода Ньютона был легко получен путем записи уравнения касательной к кривой . По сути для нахождения нового приближения функция заменялась линейной функцией (то есть раскладывалась в ряд Тейлора, при это член, содержащий вторую производную, отбрасывался, как и все последующие члены). Так же идея лежит в основе метода Ньютона для системы уравнений: функции .

Действительная функция называется аналитической в точке , если в некоторой окрестности этой точки функция разлагается в степенной ряд (ряд Тейлора):

При получаем ряд Маклорена

Разность называется остаточным членом и представляет собой ошибку при замене функции полиномом Тейлора:

Раскладываются в ряд Тейлора, причем члены, содержащие второй и более высоких порядков производные, отбрасываются. Предполагая, что функция непрерывно дифференцируема в некоторой области, содержащей и разложим левые части системы уравнений (7.3), ограничиваясь линейными членами относительно приращений: . Таким что:

(7.9)

- приближенные значения неизвестных системы, полученных на предыдущей итерации. Задача состоит в нахождении приращений (поправок).

Разложение левых частей уравнений системы (7.3):

(7.10)

… … … … … …

В правых частях значения и их производных вычисляются в точке . Поскольку в соответствии с (7.3) левые части (7.10) должны обращаться в пустое множество, приравняем к нулю и правые части, то есть найдем новое приближение из условия равенства пустого множества разложений функции .

Получим след. СЛАУ относительно приращений:

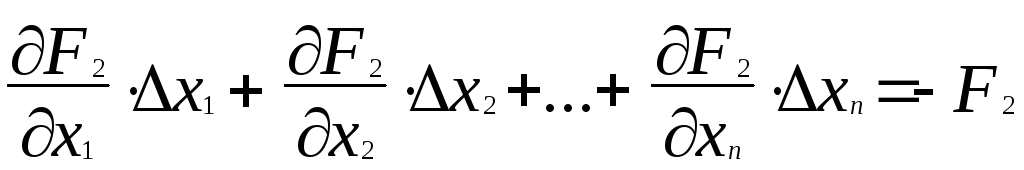(7.11)

… …

Под производной следует понимать матрицу Якоби системы функция относительно переменных

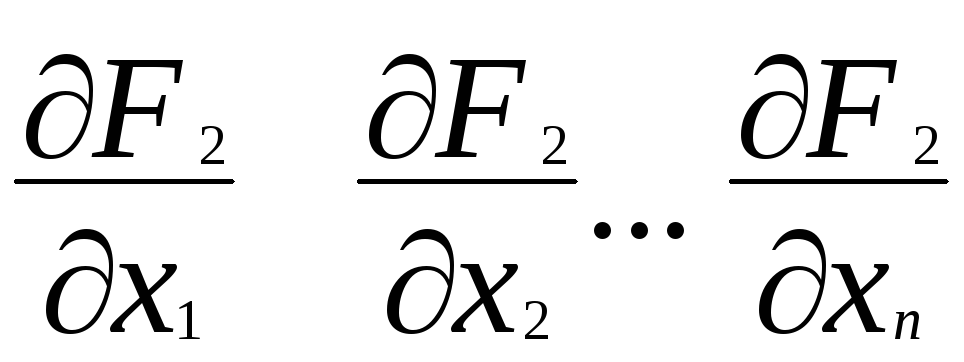(7.12)

Определитель матрицы Якоби иногда называется Якобианом: . Для существования единственного решения системы (7.11) якобиан на любой итерации. Таким образом итерационный процесс решения системы уравнений (7.3) методом Ньютона состоит в определении приращений к значениям неизвестных на каждой итерации посредством решения системы (7.11). Счет прекращается при выполнении одного из условий (7.6) – (7.8) или условия малости невязки, где . Например, условие (7.7) сведется к виду . В методе Ньютона также важен удачный выбор начала приближения для обеспечения сходимости. Сходимость ухудшается с возрастанием п.

Рассмотрим использование метода Ньютона для решения системы двух уравнений:

Пусть приближенные значения неизвестных равны .

Предположим, что якобиан системы при отличен от пустого множества, то есть:

Тогда следующие приближения неизвестных можно записать в виде:

Правые части вычисляются при .

Составим алгоритм метода Ньютона для решения системы двух уравнений. В качестве исходных данных задаются начальные приближения неизвестных , погрешность , допустимое число итераций . Если итерации сойдутся, то выводятся значения ; в противном случае текущие значения и соответствующее сообщение.

Ввод

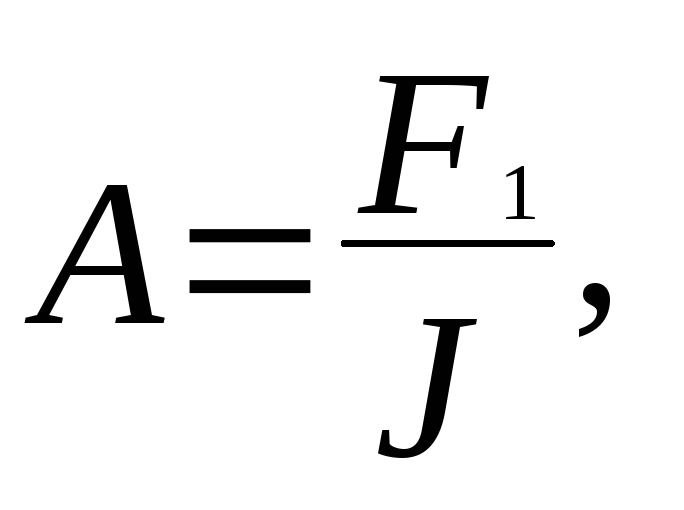
Здесь и – логическая операция, существующая во многих современных языках программирования

+ _

и

+ _

+ -

Вывод Вывод итерации

Расходятся

У Демидовича страница 452-455 рассмотрены примеры, как приближенно находятся положительные решения системы уравнений методом Ньютона.