
Лекция №7
Отступление о собственных векторах и собственных значениях матрицы.
Умножение матриц:

![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]() -
условие существования матрицы
-
условие существования матрицы
![]()
![]() ,
,
![]()
То есть, чтобы получить элемент, стоящий в i-строке и j-столбце, нужно элементы i-строки первой матрицы умножить на соответствующие элементы j-го столбца второй матрицы и полученные произведения сложить.
Свойства произведения матрицы:
(![]() -
матрицы;
-
матрицы;
![]() -
число)
-
число)

 Произведение
матриц не обладает переместительным
свойством, то есть
Произведение
матриц не обладает переместительным
свойством, то есть
![]()
Пример: ![]() 1 2
1 2 ![]() 5 6
5 6
3 4 7 8


![]() 19 22
19 22 ![]() 23 34
23 34
43 50 31 46
Может случиться, что произведения двух матриц, взятых в одном порядке, будет иметь смысл, а произведение тех же матриц, взятых в противоположном порядке, смысле иметь не будет.


Пример:
![]() 1 2 3 3 2 1
1 2 3 3 2 1
4 5 6 ![]() 2 1 3
2 1 3
 4 3 0
4 3 0
![]() 19 13 7
19 13 7
46 31 19
![]() -
не существует
-
не существует

Пусть дана квадратная матрица
![]() .
Рассмотрим линейное преобразование
.
Рассмотрим линейное преобразование
![]() (7.1)
(7.1)
![]() -
n-мерные векторы некоторого,
вообще говоря, комплексного n-мерного
пространства.
-
n-мерные векторы некоторого,
вообще говоря, комплексного n-мерного
пространства.
Определение: Ненулевой вектор называется собственным вектором данной матрицы, если в результате соответствующего линейного преобразования этот вектор переходит в коллинеарный ему, то есть если преобразованный вектор отличается от исходного только скалярным множителем.
Иначе говоря, вектор
![]() называется
собственным вектором матрицы
называется
собственным вектором матрицы
![]() ,
если эта матрица переводит вектор
,
если эта матрица переводит вектор
![]() в
вектор
в
вектор
![]() (7.2)
(7.2)
Число
![]() называется
собственным значением (или характеристическим
числом) матрицы
называется
собственным значением (или характеристическим
числом) матрицы
![]() ,
соответствующим данном собственному
вектору
,
соответствующим данном собственному
вектору
![]() .
.
Пример: Рассмотрим преобразование
проектирования в двумерном пространстве
![]() ,
определяемое матрицей:
,
определяемое матрицей:

![]() 1 0
1 0
-
0
![]()


![]()


![]()
![]()
Здесь собственными векторами являются:
-
Ненулевые векторы
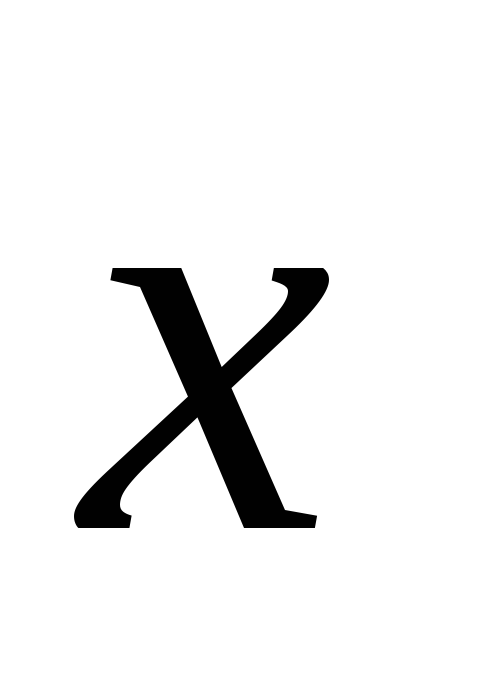 ,
направленные по оси
,
направленные по оси
 с собственным значением
с собственным значением

-
ненулевые векторы
 ,
направленные по оси
,
направленные по оси
 ,
с собственным значением
,
с собственным значением
 .
.
Уравнение (1) можно записать
![]() -
характеристическое уравнение, где
-
характеристическое уравнение, где
![]() -
характеристическая матрица
-
характеристическая матрица
![]() -
характеристический множитель.
-
характеристический множитель.
Пример:

2 1 1
![]() 1 2 1
1 2 1
1 1 2
Найти собственные значения и собственные векторы матрицы.
Решение: составим характеристическое уравнение:

![]()
![]()
![]()
![]()
Отсюда:
![]() ,
,
![]() ,
,
![]()

 Возьмем:
Возьмем:
![]() ,
подставим в уравнение
,
подставим в уравнение
![]() .
.
Имеем: 1 1 1 x1
1 1 1 ![]() x2
x2 ![]()
1 1 1 x3
Или
![]()

![]()
![]()
Достаточно решить одно из этих уравнений:
положив
![]() ;
;![]() ,
получим
,
получим
![]() ,
где
,
где
![]() и
и
![]() -
любые числа не равные пустому множеству
одновременно.
-
любые числа не равные пустому множеству
одновременно.
В
 частности, выбирая сперва
частности, выбирая сперва
![]() ,
,
![]() ,
а затем
,
а затем
![]() ,
,
![]() будем
иметь простейшую фундаментальную.
Систему решений, состоящую из двух
линейно независимых векторов матрицы
будем
иметь простейшую фундаментальную.
Систему решений, состоящую из двух
линейно независимых векторов матрицы
![]() :
:
1 0
![]() 0 и
0 и ![]() 1
1
-1 -1
Все остальные собственные векторы
матрицы
![]() соответствующие
характеристическому числу
соответствующие
характеристическому числу
![]() ,
являются линейной комбинацией этих
базисных векторов и заполняют плоскость,
натянутую на векторы
,
являются линейной комбинацией этих
базисных векторов и заполняют плоскость,
натянутую на векторы![]() и
и
![]() (исключая начало координат).
(исключая начало координат).
Возьмем теперь
![]() .
Подставляя это значение в уравнение,
получим:
.
Подставляя это значение в уравнение,
получим:


-2 1 1 x1
1 -2 1 ![]() x2
x2 ![]()
1 1 -2 x3
Или
![]()

![]()
![]()
Отсюда:
![]() -
постоянная, отличная от пустого
множества. Положим
-
постоянная, отличная от пустого
множества. Положим
![]() ,
получим простейшее решение, реализующее
собственный вектор матрицы
,
получим простейшее решение, реализующее
собственный вектор матрицы
![]()

1
![]() 1
1
1
Задача нахождения собственных значений
и собственных векторов возникает во
многих задачах механики, физики и химии.
С точки зрения линейной алгебры задача
о собственных значениях и векторах
включает в себя составление
характеристического мн-на, отыскание
корней этого мн-на (собственных
значений), однородной системы, то есть
определение собственных векторов
матрицы
![]() .
.
В рассмотренных метода на каждой итерации
исходная функция аппроксимируется
линейной функцией. Для итерации формул
можно использовать информацию о функции
в нескольких точках, предшествующих
точке
![]() .
Например, в методе парабол по трем
последовательным приближениям строится
мн-н второй степени (парабола),
приближающий исходную функцию. Этот
метод называется n-дополнительных
парабол, меьод Мюллера, или методом
квадратичной интерполяции.
.
Например, в методе парабол по трем
последовательным приближениям строится
мн-н второй степени (парабола),
приближающий исходную функцию. Этот
метод называется n-дополнительных
парабол, меьод Мюллера, или методом
квадратичной интерполяции.
