- •Лабораторная работа №4 исследование индуктивной катушки и конденсатора цель работы
- •Основные теоретические положения
- •Объект и средства исследования
- •Порядок проведения эксперимента
- •1.Исследование индуктивной катушки в цепи постоянного тока
- •2.Исследование индуктивной катушки в цепи переменного тока
- •3. Исследование конденсатора в цепи постоянного тока
- •4.Исследование конденсатора в цепи переменного тока
- •Обработка результатов эксперимента
- •Контрольные вопросы и задачи
- •Протокол испытаний к лабораторной работе №4 "Исследование индуктивной катушки и конденсатора"
- •1. Исследовательская часть
- •2. Расчётно-графическая часть
Лабораторная работа №4 исследование индуктивной катушки и конденсатора цель работы
1.Получить навыки экспериментального определения параметров индуктивной катушки и конденсатора.
2.Освоить методы анализа электрической цепи синусоидального тока состоящей из индуктивной катушки или конденсатора.
Основные теоретические положения
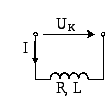
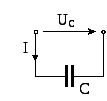
В данной работе исследуются отдельные элементы цепей синусоидального тока – индуктивная катушка с постоянными параметрами R и L (рис.1), а также конденсатор переменной ёмкости С (рис.2).
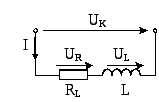
При анализе цепи индуктивную катушку представляют в виде эквивалентной схемы замещения, представляющей собой последовательной соединение резистивного элемента c сопротивлением RL, равным активному сопротивлению катушки и индуктивного элемента с индуктивностью L, равной индуктивности катушки (рис. 3).
|
|
|
|
|
Рис. 1 |
Рис. 2 |
Рис. 3 |
Полное сопротивление катушки
Zк=Uк/I, (4.1)
где UкиI– соответствующие значения напряжения и тока катушки.
Полное сопротивление связано с сопротивлениями схемы замещения следующей формулой:
![]() ,
(4.2)
,
(4.2)
где ![]() – активное сопротивление катушки;
– активное сопротивление катушки;
ХL=ωL= 2πfL– индуктивное сопротивление катушки;
ω= 2πf– угловая частота;
f –частота тока в цепи (f= 50Гц).
Полное сопротивление катушки можно представить как гипотенузу прямоугольного треугольника сопротивлений (рис. 4), один катет которого равен RL, а другой ХL.
|
|
Из треугольника сопротивлений следуют расчётные формулы:
|
|
Рис. 4 Треугольник сопротивлений катушки |
В
соответствии со вторым законом Кирхгофа
вектор напряжения индуктивной катушки
![]() определяется выражением:
определяется выражением:
![]() .
(4.6)
.
(4.6)
Вектор
напряжения на резистивном элементе UR
(активная составляющая вектора UK)
совпадает по направлению с вектором
тока I. Вектор
напряжения на индуктивном элементе UL.
(реактивная составляющая вектора UK)
опережает вектор тока I
на угол 90°. Действующие значения
напряжений
![]() и UL,
тока I и соответствующие
сопротивления катушки связаны следующими
формулами:
и UL,
тока I и соответствующие
сопротивления катушки связаны следующими
формулами:
UR =RL×I; UL = XL×I. (4.7)
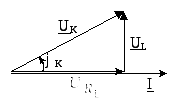
Вектор напряжения индуктивной катушки UK опережает вектор тока I на угол φк (0 < φк < 90°). Векторная диаграмма тока и напряжений индуктивной катушки приведена на рис. 5.
|
|
Векторы
напряжений Uк,
|
|
Рис. 5 Векторная диаграмма тока и напряжений индуктивной катушки |
![]() ;
(4.8)
;
(4.8)
![]() ;
(4.9)
;
(4.9)
![]() (4.10)
(4.10)
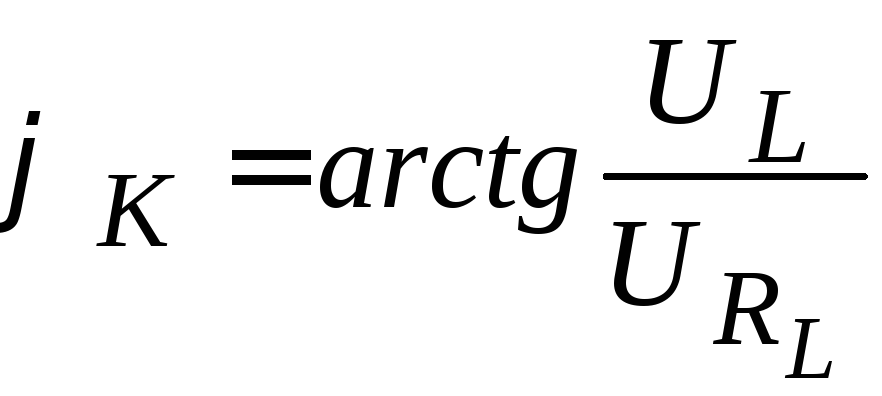 .
(4.11)
.
(4.11)
Полная мощность катушки Sк по определению равна произведению действующих значений напряжения на катушке UK и тока катушки I, т.е.
Sк=Uк·I. (4.12)
Учитывая, что Uк = Zк·I , получаем Sк = Zк·I2.
Полная мощность Sк связана с активной Р и реактивной QL мощностями индуктивной катушки выражением
![]() .
(4.13)
.
(4.13)
Активная мощность Р численно равна электрической энергии, преобразующейся в катушке в теплоту за единицу времени, и определяется формулами:
![]() .
(4.14)
.
(4.14)
Реактивная мощность QL численно равна амплитуде мгновенной мощности, находящейся в процессе обмена между магнитным полем катушки и источником электрической энергии. Величина. реактивной мощностиQL. определяется формулами:
![]() .
(4.15)
.
(4.15)
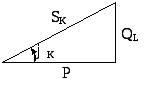
Графическая связь между полной мощностью SK, активной мощностью Р и реактивной мощностью QL можно представить в виде прямоугольного треугольника мощностей (рис.6), гипотенуза которого равна SK, а катеты Р и QL.
|
|
Треугольник мощностей подобен треугольникам сопротивлений и напряжений. Из данного треугольника вытекают следующие соотношения:
|
|
Рис. 6 – Треугольник мощностей |
![]() ;
;
![]() .
(4.16)
.
(4.16)
Из треугольника мощностей (рис. ) следует:
![]() .
(4.17)
.
(4.17)
Поэтому величину cosφк называют коэффициентом мощности, т.к. он показывает: какую часть активная мощность Р составляет от полной мощности S.
При исследовании конденсатора его представляют, пренебрегая потерями, в виде ёмкостного элемента, обладающего ёмкостью С.
Ёмкостное сопротивление конденсатора
![]() ,
(4.18)
,
(4.18)
где UCиI– действующие значения напряжения и тока конденсатора.
Величина ХC зависит от ёмкости конденсатора С и частоты протекающего в нём тока.
 (Ом).
(4.19)
(Ом).
(4.19)
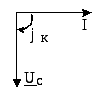
Векторная диаграмма тока и напряжения конденсатора приведена на рис. 7. На ней видно, что вектор напряжения на ёмкостном элементе UC отстает от вектора тока I на угол 90 градусов.
|
|
В электрической цепи с ёмкостным элементом работа не совершается, поэтому активная мощность Р, потребляемая ёмкостным элементом, равна нулю. Однако, в цепи происходит периодический обмен энергией между источником и ёмкостным элементом. |
|
Рис. 7 – Векторная диаграмма тока и напряжения конденсатора |
Интенсивность такого обмена характеризуют реактивной мощностью
![]() .
(4.20)
.
(4.20)


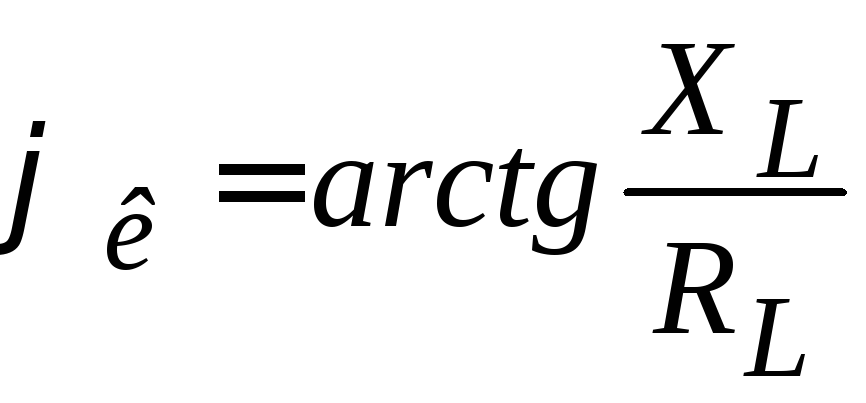 .
(4.5)
.
(4.5)