
LK / Лекция 21
.docБаранов Виктор Павлович. Дискретная математика.
Раздел 4. Функциональные системы с операциями. Алгебра логики.
Лекция 21. Принцип двойственности. Разложение функций по переменным. Совершенные ДНФ и КНФ

Лекция 21. ПРИНЦИП ДВОЙСТВЕННОСТИ. РАЗЛОЖЕНИЕ БУЛЕВЫХ
ФУНКЦИЙ ПО ПЕРЕМЕННЫМ. СОВЕРШЕННЫЕ ДИЗЪЮНКТИВНАЯ И
КОНЪЮНКТИВНАЯ НОРМАЛЬНЫЕ ФОРМЫ
План лекции:
-
Принцип двойственности.
-
Разложение булевых функций по переменным. Совершенные дизъюнктивная и конъюнктивная нормальные формы.
-
Принцип двойственности
Функция
![]() ,
равная
,
равная
![]() ,
называется двойственной функцией
к функции
,
называется двойственной функцией
к функции
![]() .
.
Очевидно, что таблица истинности для
двойственной функции
![]() получается из таблицы истинности для
функции
получается из таблицы истинности для
функции
![]() инвертированием (т. е. заменой 0 на 1 и 1
на 0) значений переменных и функции.
Например,
инвертированием (т. е. заменой 0 на 1 и 1
на 0) значений переменных и функции.
Например,
![]() .
.
Легко установить для функций 0, 1,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
что
,
что
-
функция 0 двойственна 1;
-
функция 1 двойственна 0;
-
функция
 двойственна
двойственна
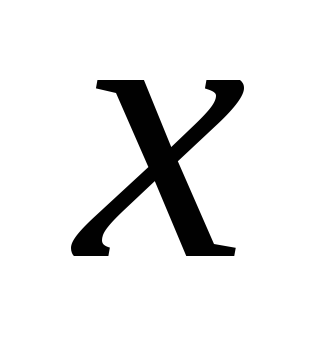 ;
; -
функция
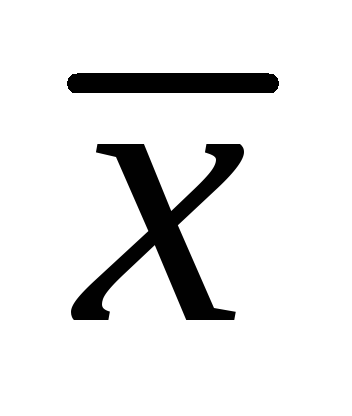 двойственна
двойственна
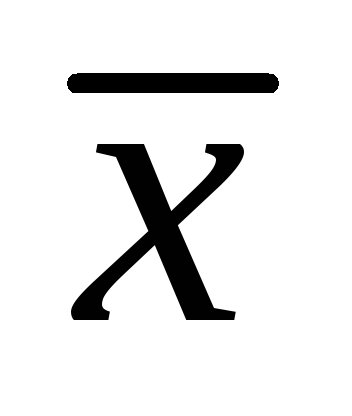 ;
; -
функция
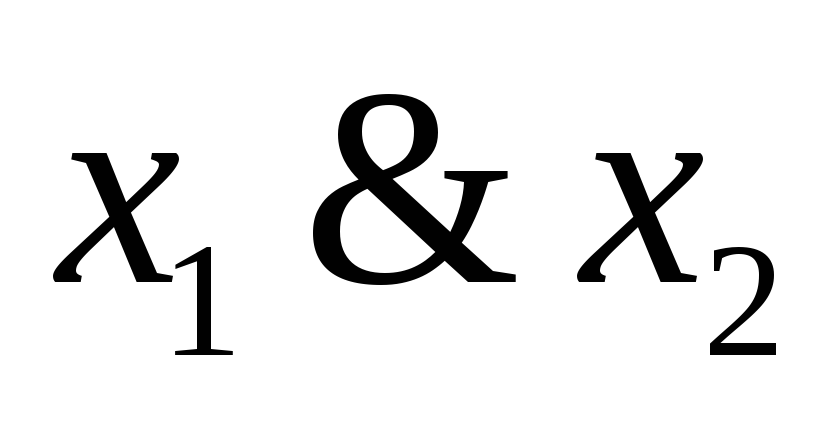 двойственна
двойственна
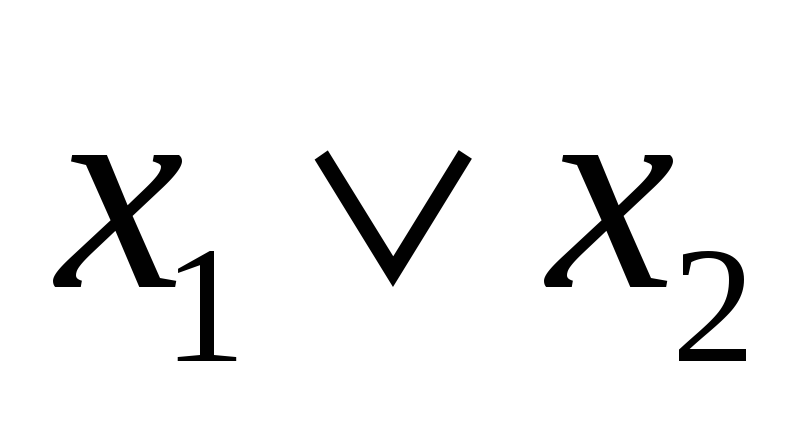 ;
; -
функция
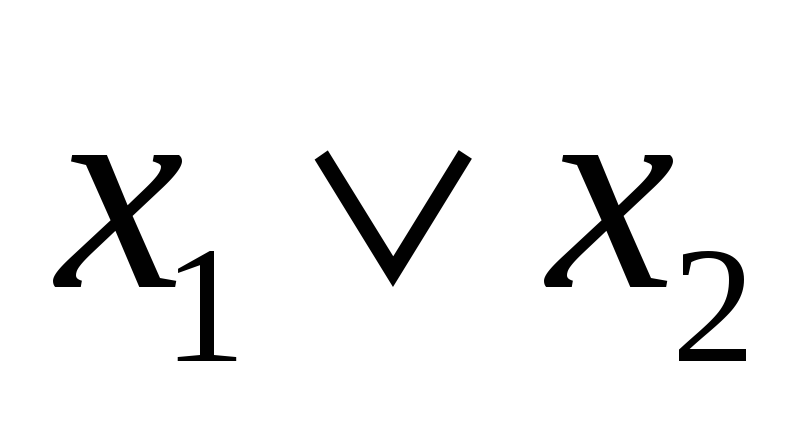 двойственна.
двойственна.
Из определения двойственности следует, что
![]() ,
,
т. е. функция
![]() является двойственной к
является двойственной к
![]() (свойство взаимности).
(свойство взаимности).
Принцип двойственности. Если формула
![]() реализует функцию
реализует функцию
![]() ,
то формула
,
то формула
![]() ,
т. е. формула, полученная из
,
т. е. формула, полученная из
![]() заменой функций
заменой функций
![]() соответственно на
соответственно на
![]() ,
реализует функцию
,
реализует функцию
![]() .
.
Формулу
![]() будем называть формулой, двойственной
к
будем называть формулой, двойственной
к
![]() .
.
Для доказательства этого утверждения
необходимо проверить его справедливость
для элементарных шагов суперпозиции
![]() и
и
![]() .
.
Пусть, например, функция
![]() получается из функции
получается из функции
![]() в результате следующей подстановки
переменных
в результате следующей подстановки
переменных
![]() :
:
![]() .
.
Тогда
![]()
т. е. функция
![]() получается из
получается из
![]() в результате той же самой подстановки
переменных.
в результате той же самой подстановки
переменных.
Доказательство справедливости принципа
двойственности для шага
![]() проведем на примере. Пусть
проведем на примере. Пусть
![]() .
.
Тогда

т. е. функция
![]() получается из
получается из
![]() и
и
![]() так же, как функция
так же, как функция
![]() из
из
![]() и
и
![]() .
.
Принцип двойственности позволяет упростить вывод основных тавтологий и имеет целый ряд полезных применений, которые будут рассмотрены далее.
Пример 1. Из тождества
![]() следует тождество
следует тождество
![]() .
.
Действительно,
![]() ;
;![]() ;
;
![]() .
.
Пример 2. Построение формулы для отрицания функции.
Из определения двойственной функции следует
![]() .
.
Получаем следующее правило: пусть
формула
![]() реализует функцию
реализует функцию
![]() .
Чтобы получить формулу для функции
.
Чтобы получить формулу для функции
![]() нужно в формуле
нужно в формуле
![]() заменить все переменные на их отрицания.
заменить все переменные на их отрицания.
Найдем отрицание для функции![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
-
Разложение булевых функций по переменным. Совершенные
дизъюнктивная и конъюнктивная нормальные формы
Введем обозначение
![]() ,
,
где
![]() – параметр, равный либо 0, либо 1. Очевидно,
что
– параметр, равный либо 0, либо 1. Очевидно,
что
![]()
Легко видеть, что
![]() 1
тогда и только тогда, когда
1
тогда и только тогда, когда
![]() .
.
Теорема о разложении
функций по переменным. Каждую функцию
алгебры логики
![]() при любом
при любом
![]() (
(![]() )
можно представить в следующей форме:
)
можно представить в следующей форме:
![]() ,
(1)
,
(1)
где дизъюнкция берется по всевозможным
наборам значений переменных
![]() .
.
Это представление называется разложением
функции по
![]() переменным
переменным
![]() .
.
Доказательство.
Рассмотрим произвольный набор
значений переменных
![]() и покажем, что левая и правая части
соотношения (1) принимают на нем одно и
то же значение. Левая часть дает
и покажем, что левая и правая части
соотношения (1) принимают на нем одно и
то же значение. Левая часть дает
![]() .
Правая –
.
Правая –

В качестве следствий из теоремы рассмотрим два специальных случая разложения.
-
Разложение по переменной:
![]() .
.
Функции
![]() и
и
![]() называются компонентами разложения.
Данное разложение полезно, когда
какие-либо свойства устанавливаются
по индукции.
называются компонентами разложения.
Данное разложение полезно, когда
какие-либо свойства устанавливаются
по индукции.
-
Разложение по всем
 переменным:
переменным:
![]() .
.
При
![]() тождественно не равной 0 оно может быть
преобразовано:
тождественно не равной 0 оно может быть
преобразовано:
![]() .
.
В результате окончательно получим
![]() .
(2)
.
(2)
Такое разложение называется совершенной дизъюнктивной нормальной формой (совершенной д. н. ф.).
Непосредственно к понятию совершенной д. н. ф. примыкает следующая теорема.
Теорема. Каждая
функция алгебры логики может быть
представлена формулой в базисе![]() .
.
Доказательство.1)
Пусть
![]() .
Тогда, очевидно,
.
Тогда, очевидно,
![]() .
.
-
Пусть
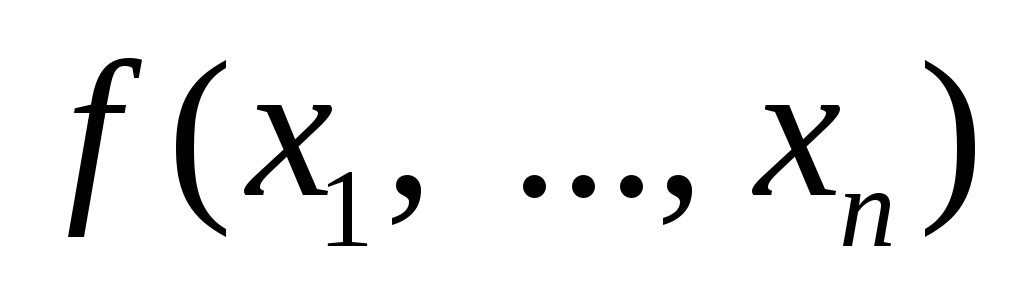 тождественно не равна 0. Тогда ее можно
представить формулой (2).
тождественно не равна 0. Тогда ее можно
представить формулой (2).
Данная теорема носит конструктивный
характер, так как она позволяет для
каждой функции построить реализующую
ее формулу в виде совершенной д. н. ф.
Для этого в таблице истинности для
каждой для функции
![]() отмечаем все строки
отмечаем все строки
![]() ,
в которых
,
в которых
![]() .
Для каждой такой строки образуем
логическое произведение
.
Для каждой такой строки образуем
логическое произведение
![]() ,
а затем все полученные конъюнции соединим
знаком дизъюнкции.
,
а затем все полученные конъюнции соединим
знаком дизъюнкции.
Пример 3. Найти совершенную д.
н. ф. для функции
![]() .
.
|
|
|
|
0 0 |
1 |
|
0 1 |
1 |
|
1 0 |
0 |
|
1 1 |
1 |
Совершенная д. н. ф. есть выражение типа
![]() П. Покажем, что при
П. Покажем, что при
![]() тождественно не равной 1 ее можно
представить в виде
тождественно не равной 1 ее можно
представить в виде
![]() .
Запишем для двойственной функции
(очевидно не равной тождественно 0)
разложение в виде совершенной д. н. ф.:
.
Запишем для двойственной функции
(очевидно не равной тождественно 0)
разложение в виде совершенной д. н. ф.:
![]() .
.
Из принципа двойственности следует
![]() .
.
Таким образом, получаем разложение, которое называется совершенной конъюнктивной нормальной формой (совершенной к. н. ф.):
![]() .
(3)
.
(3)
Пример 4. Построить совершенную
к. н. ф. для функции
![]() .
.
Имеем
![]() .
.
