LK / Лекция 14

Баранов Виктор Павлович. Дискретная математика. Раздел 3. Графы, сети, коды.

Лекция 14. Алгоритм построения максимального потока в транспортной сети

Лекция 14. АЛГОРИТМ ПОСТРОЕНИЯ МАКСИМАЛЬНОГО ПОТОКА В ТРАНСПОРТНОЙ СЕТИ

План лекции:

1. Определение прибавляющей цепи.

2. Алгоритм построения максимального потока в транспортной сети.

1. Определение прибавляющей цепи

Из теоремы Форда-Фолкерсона следует, что максимальный поток в сети не превосходит минимальной пропускной способности разреза, то есть

. (1)

Анализ неравенства (1) показывает, что величина потока совпадает с пропускной способностью разреза тогда и только тогда, когда выполняется условие:

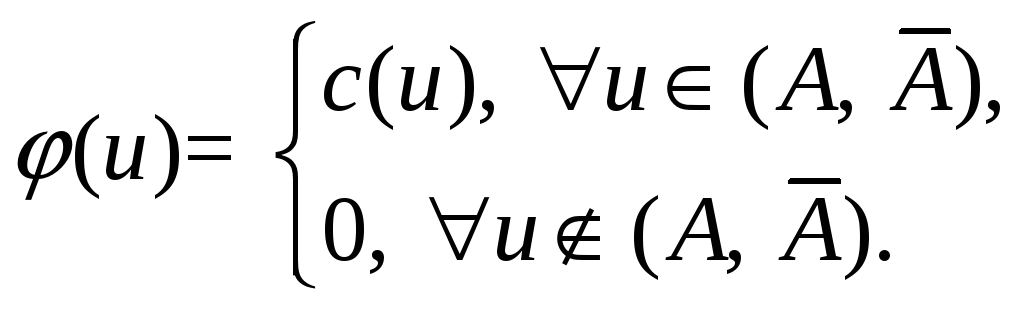(2)

Алгоритм, который приводится ниже, направлен на построение такого разреза, для которого выполняется условие (2). Если удается построить такой разрез, то задача решена, если нет, то производится увеличение потока с помощью прибавляющих цепей.

Дадим определение прибавляющей цепи. Рассмотрим в сети цепь из источника в сток, то есть последовательность вершин

такую, что между вершинами и есть дуга (), которой может оказаться прямой или обратной .

Пусть в сети задан поток . Цепь из в называется прибавляющей, если для каждой ее прямой дуги выполняется строгое неравенство , а для каждой обратной дуги – строгое неравенство .

Предположим, что для потока удалось найти прибавляющую цепь. Тогда увеличивая на максимально возможное число единиц на прямых дугах (с обеспечением условия ) и уменьшая на столько же единиц на обратных дугах (с обеспечением условия ), получим новый поток, величина которого на единиц больше, чем величина .

Пример 1. Пусть прибавляющая цепь имеет вид (рис. 1):

5, 3 6, 2 2, 2 4, 2 7, 3 5, 2 6, 4

Рис.1.

С помощью это цепи можно перейти к новому потоку (рис. 2.):

5, 5 6, 4 2, 0 4, 4 7, 1 5, 4 6, 6

Рис. 1.

2. Алгоритм построения максимального потока в транспортной сети

Алгоритм состоит в последовательном просмотре вершин сети и присвоении им отметок. На каждом шаге алгоритма любая вершина находится в одном из трех состояний: а) не помечена; б) помечена, но не просмотрена; в) помечена и просмотрена.

0-й шаг. Зададим какой-нибудь, например, нулевой поток по сети.

1-й шаг. Помети источник любой отметкой, например, звездочкой *. После этого вершина помечена, но не просмотрена. Остальные вершины не помечены.

2-й шаг. Берем очередную помеченную, но не просмотренную вершину . Просматриваем все дуги, инцидентные этой вершине. Если вторая вершины дуги не помечена, то помечаем ее отметкой в следующих двух случаях:

а) дуга выходит из вершины и поток по ней строго меньше пропускной способности;

б) дуга входит в вершину и поток по ней строго больше нуля.

После завершения этого шага вершина объявляется помеченной и просмотренной, а вершины, получившие при просмотре отметку , объявляются помеченными, но не просмотренными.

Шаг 2 циклически повторяется до тех пор, пока не произойдет одно из двух событий, рассматриваемых далее на 3-ем и 4-ом шагах.

3-й шаг. Сток получил отметку, например, . Переходим из в вершину , по отметке вершины отыскиваем следующую вершину и т. д. до тех пор, пока не дойдем до вершины . В результате получаем прибавляющую цепь, с помощью которой увеличиваем текущий поток. Далее стираем отметки всех вершин и повторяем выполнение алгоритма с 1-го шага.

4-й шаг. Процесс расстановки отметок закончился тем, что все помеченные вершины просмотрены, но сток при этом не помечен. Пусть – множество помеченных вершин. Так как , а , то можно определить разрез . Для , то есть дуги, идущей из помеченной вершины в непомеченную, , иначе другой конец этой дуги был бы помечен. По той же причине для . Следовательно, для построенного потока и разреза , образованного помеченными вершинами, выполняются условия (1). В таком случае имеем максимальный поток.

Пример 2. Пусть задана транспортная сеть и поток по ней (рис. 2).

5, 3

10, 7 4, 4 5, 5

3, 2

6, 4 2, 2

5, 5 6, 2

2, 2 9, 5

3, 3

Рис. 2.

Процесс расстановки отметок показан в таблице 1.

Таблица 1

Номер шага	Отметки вершин
1	*
2	*
3	*
4	*
5	*
6	*
7	*

Поскольку сток получил отметку, то строим прибавляющую цепь (рис. 3).

10, 7 5, 3 3, 2 6, 4 6, 2 9, 5

Рис. 3.

Увеличиваем поток на две единицы на прямых дугах этой цепи и уменьшаем на две единицы на обратных. В результате получаем поток, изображенный на рис. 4.

5, 5

10, 9 4, 4 5, 5

3, 0

6, 2 2, 2

5, 5 6, 4

2, 2 9, 7

3, 3

Рис. 4.

В процессе расстановки отметок для нового потока удается пометить только вершины и . Тогда – множество помеченных вершин, которое порождает минимальный разрез . Его пропускная способность

совпадает с величиной потока

или

.

3