Амплитудная модуляция

Колебания носителя гармонических видов модуляции можно представить в следующем виде:

где и— соответственно постоянные амплитуда, круговая частота и начальная фаза гармонического колебания.

Модулирующую функцию, т. е. закон изменения информацион­ного сигнала обозначают . При амплитудной модуляции моду­лирующий сигнал воздействует на постоянную амплитуду колебаний переносчика, к которой будет добавляться перемен­ная, изменяющаяся пропорционально модулирующему сигналу:

где - наибольшее отклонение амплитуды АМ-колебания.

С учетом этого АМ-колебание запишется

(2.12)

где отношение называется коэффициентом амплитуд­ной модуляции. Во избежание перемодуляции, когда на выходе модулятора резко расширяется спектр модулирующего сигнала,не должен превышать единицы.

Выражение (2.12) можно записать так:

(2.13)

Если модулирующая функция представляет собой гармоническое колебание одной частоты с единичной амплитудой (рис. 2.9,а), то при AM согласно (2.10)

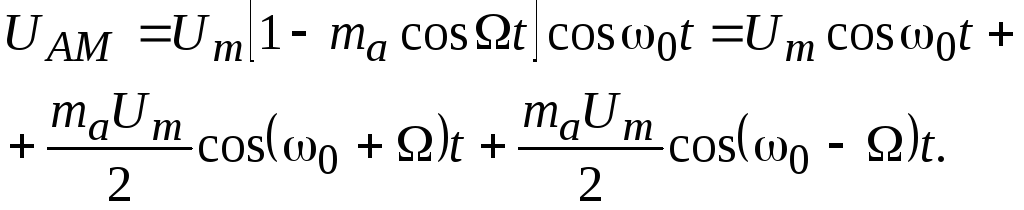(2.14)

Здесь первое слагаемое описывает не модулируемое колебание несущей частоты, второе и третье слагаемое с частотами иназываются соответственно верхней и нижней боковыми частотами. На рис. 2.9, б представлен график напряжения несу­щей частоты, модулированного по амплитуде по закону информа­ционного сигнала. Спектр АМ-сигнала для рассматривае­мого случая, который можно получить, используя преобразование Фурье, содержит несущую и две боковые частоты (рис. 2.9, в). Ширина спектра при этом равна .

При модуляции несущей частоты сложным сигналом, имеющим широкий спектр частот, АМ-колебание будет содержать верхнюю и нижнюю боковые полосы частот (рис. 2.9, г). При этом ширина спектра определяется значением удвоенной максимальной частоты спектра модулирующего сигнала

Рис. 2.9. Графики модулирующего (а) и модулированного (б) сигналов; спектры амплитуд амплитудно-модулированных сигналов для простого (в) и сложного (г) модулирующих сигналов.

Рис. 2.10. Амплитудная манипуляция: а – модулирующий сигнал; б – амплитудно-манипулированный сигнал при ; в – при; г – спектр модулирующего сигнала; д – спектр амплитудно-манипулированного сигнала.

Лекция 3 Частотная модуляция

При частотной модуляции амплитуда модулируемого напряже­ния остается постоянной, а частота несущей частоты изменяется во времени относительно своего центрального значения по закону изменения первичного сигнала f(t):

(2.15)

где — наибольшее отклонение угловой частоты от централь­ного значения , называемое девиацией частоты.

Отношение называется индексом частотной модуляции. Так как в выражение для модулируемого сигнала входит постоян­ная частота, то амплитуду колебания переносчика можно описать выражением

(2.16)

где — фаза колебания, связанная с частотой соотношением

Форма ЧМ-сигнала с постоянной амплитудой представлена на рис. 2.11, а. При ЧМ фаза колебания

(2.17)

Рис. 2.11. Частотно-модулированный сигнал (а) и его спектр (б) Рис. 2.12. Частотная манипуляция: а - модулирующий сигнал, б -частотно-манипулированный сигнал, в и г – амплитудно-манипулированные сигналы, д – спектр частотно-манипулированного сигнала.

Подставив выражение (2.17) в (2.16), получим

(2.18)

При модуляции несущей модулирующим колебанием одной частоты спектр ЧМ-сигнала (рис. 2.11, б), как и при АМ, состоит из несущей частоты и двух боковых полос, но каждая боковая полоса содержит бесконечную последовательность гармонических колебаний, отстоящих друг от друга на , причем амплитуда k-го колебания (k=1, 2, 3, ...), считая от модулируемого сигнала , пропорциональна значению функции Бесселя первого родаk-го порядка при аргументе, равном индексу частотной мо­дуляции .

Так как амплитуда боковых составляющих убывает по мере удаления от несущей частоты, то практически ширину спектра всегда ограничивают частотными составляющими, амплитуды которых не меньше некоторой определенной величины (5—10% амплитуды несущей частоты V_т до модуляции).

Приближенно ширину спектра ЧМ-сигнала можно определить из выражения

(2.19)

Видно, что чем меньше индекс частотной модуляции , тем уже практически необходимый спектр ЧМ-сигнала.

В зависимости от выбранного индекса модуляции различают узкополосную частотную модуляцию с малыми индексами и широкополосную — с большими индексами . При узкополосной ЧМ ширина спектра приближается к АМ, а при широкополосной — много больше, чем при АМ.

Основным преимуществом широкополосной ЧМ является высокая помехоустойчивость, значительно большая, чем при АМ, так как частота сигнала менее подвержена действию помех, чем, амплитуда.

При частотной манипуляции в качестве информационного сиг­нала используется последовательность прямоугольных импульсов (рис. 2.12, а). При этом ЧМ-сигнал имеет два граничных значения частоты: (рис. 2.12,б) . Если представить ЧМ-сигнал суммой двух сигналов U₁ и U₂ с амплитудной манипуля­цией (рис. 2.12, в, г), то легко определить спектр сигнала при частотной манипуляции (рис 2.12, д).

Необходимая ширина спектра частотно-манипулированного сиг­нала будет равна , что больше, чем при амплитуд­ной манипуляции на величину.