3.3.1. Линейная парная регрессия

Рассмотрим связь между одной причиной и следствием, то есть парную регрессию (однофакторную регрессионную модель). В этом случае исходными данными являютсязначений() фактораи соответствующие значения() результативной величины.

Предположим, что связь между и описывается линейной функцией

.

Для отдельного наблюдения имеем соотношение: , где и – коэффициенты регрессии; – независимая нормально распределенная случайная величина – остаток с нулевым математическим ожиданием и постоянной дисперсией.

Если , то переменныеХ и Y положительно коррелированы, если , то – отрицательно коррелированы;

Случайная величина отражает тот факт, что изменение будет неточно описываться изменением (присутствуют другие факторы, не учтенные в данной модели).

Оценка параметров уравнения парной регрессии

_{Для линейной регрессионной модели критерий метода наименьших квадратов запишется в виде:}

Нахождение параметров регрессионного уравнения приводит к следующей системе линейных алгебраических уравнений:

_или

Решая эту систему двух уравнений с двумя неизвестными, получаем

;

.

Можем записать

Такое решение может существовать только при выполнении условия

.

Это условие называется условием идентифицируемости модели и означает, что не все значения совпадают между собой. Принарушении этого условия все точки () лежат наодной вертикальной прямой .

Выражение для b можно записать и в другом виде

В случае системы двух нормальных случайных величин и линейной связи между ними имеем уравнения регрессиинаинасоответственно (рис.5.3.):

;

где – среднее значений величины при значении;

–среднее значений величины при значении;

Рис. 3.3.3. Графическое представление уравнений регрессии

Оценка качества линейного уравнения парной регрессии

Для оценки качества парной линейной регрессионной модели целесообразно:

1) вычислить и оценить значимость коэффициента корреляции;

2) проверить адекватность (значимость) всей модели регрессии;

3) оценить среднее квадратическое отклонение остатков ;

4) проверить значимость параметров а и b модели регрессии;

5) определить доверительные границы модели регрессии;

6) определить интервальные оценки параметров а и b модели регрессии.

Для проверки значимости модели парной линейной регрессии используется F–критерий Фишера:

.

В качестве меры точности парной линейной регрессии применяют стандартную ошибку

С помощью величины можно построить доверительные границы для уравнения регрессии.

Проведем анализ значимости параметров модели парной линейной регрессии .

Наблюдаемые значения , соответствующие данным,являются случайными. Случайными являются и рассчитанные по ним значения коэффициентов а и b. Надежность получаемых оценок а и b зависит от дисперсии случайных отклонений (ошибок).

По данным выборки эти отклонения и соответственно их дисперсия не оцениваются, а используются отклонения зависимой переменной от ее расчетных значений :

.

Так как предполагается, что ошибки (остатки) _i нормально распределены, то среднеквадратическое отклонение ошибок используется для измерения вариации параметров регрессионной модели. Среднеквадратические отклонения коэффициентов определяются по формулам:

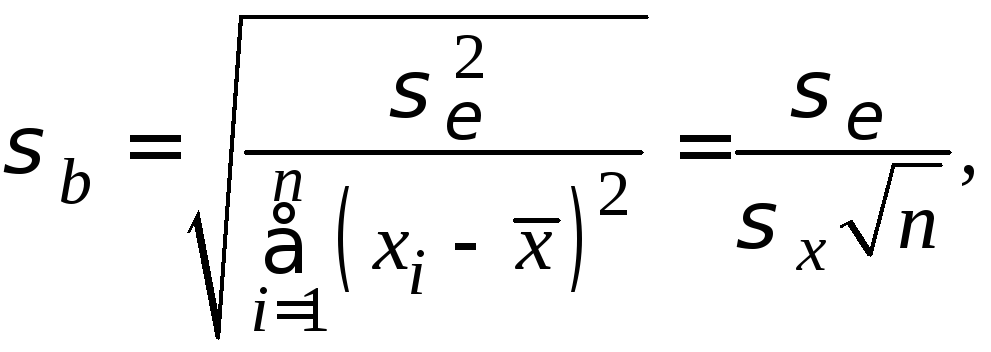
где – оценка математического ожидания (среднее значение) независимой переменной Х; – стандартная ошибка оценки регрессии.

Проверка значимости отдельных коэффициентов регрессии связана с определением наблюдаемых (расчетных) значений Т–критерия (Т–статистики) для соответствующих коэффициентов регрессии. Нулевая (проверяемая) гипотеза в данном случае имеет вид:

Наблюдаемые значения критерия и сравниваются с табличными (при двухсторонней критической области)

Если расчетное значение критерия превосходит его табличное значение при заданном уровне значимости  (0.1; 0.05; 0.01), коэффициент регрессии считается значимым.

В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится).

Для значимого уравнения регрессии представляет интерес построение интервальных оценок для параметра b и свободного члена а

; ,

где определяется по таблице распределения Стьюдента для уровня значимости  и числа степеней свободы ν = п –2; – стандартные отклонения свободного члена и коэффициента регрессии соответственно; n – число наблюдений.