
- •Иванов в.И.
- •Лекция 1 Два определения интеграла Римана по прямоугольнику. Критерий Коши
- •1. Два определения интеграла Римана по прямоугольнику
- •2. Критерий Коши
- •2. Колебание функции по прямоугольнику и в точке. Критерий непрерывности функции в точке
- •3. Замкнутость множества точек, в которых колебание функции не меньше заданного положительного числа
- •1. Измеримость множества по Жордану в r2. Критерий измеримости
- •2.Достаточное условие измеримости
- •3. Определение двойного интеграла Римана по измеримой по Жордану области. Достаточное условие интегрируемости
- •Лекция 6
- •Лекция 8
- •2. Ортогональные криволинейные координаты. Якобиан в случае ортогональных координат
- •2. Сферические координаты в Rn. Их ортогональность
- •2. Сходимость кратных интегралов
- •3. Кратные несобственные интегралы 2-го рода. Абсолютная сходимость.
- •4. Сходимость кратных интегралов
- •2. Приложения криволинейного интеграла 1-го рода
- •Лекция 16 Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в r2
- •1. Криволинейный интеграл 2-го рода. Его физический смысл
- •2. Формула Грина
- •3. Условия независимости интеграла от пути в r2
- •Лекция 17 Площадь поверхности в r3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
- •1. Площадь поверхности в r3
- •2. Поверхностный интеграл 1-го рода. Его свойства, вычисление
- •2. Связь поверхностного интеграла 2-го рода с интегралом 1-го рода
- •Лекция 20 Скалярное и векторное поля. Поток, дивергенция, циркуляция и ротор векторного поля. Векторные линии и векторные трубки
- •1. Скалярное и векторное поля
- •2. Поток, дивергенция, циркуляция и ротор векторного поля
- •3. Векторные линии и векторные трубки
- •Лекция 21
- •Лекция 23 Дифференциальные формы. Замена переменных в дифференциальной форме. Дифференциал от дифференциальной формы. Второй дифференциал. Замкнутые и точные дифференциальные формы
- •1. Дифференциальные формы. Замена переменных в дифференциальной форме
- •2. Дифференциал от дифференциальной формы. Второй дифференциал
- •2. Площадь поверхности сферы в Rn
- •Лекция 25 Ориентация на поверхности и ее границе. Интегрирование дифференциальной формы по ориентированной поверхности
- •1. Ориентация на поверхности и ее границе
- •2. Интегрирование дифференциальной формы по ориентированной поверхности
Лекция 16 Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в r2
1. Криволинейный интеграл 2-го рода. Его физический смысл
Пусть
 - гладкая кривая,
- гладкая кривая,
![]() .
.
Пусть
![]() - разбиение отрезка
- разбиение отрезка![]() ,
,
![]() -
мелкость разбиения,
-
мелкость разбиения,
![]() -
-![]() разметка
разбиения.
разметка
разбиения.
Образуем следующую интегральную сумму:
 Будем
говорить, что для функций
Будем
говорить, что для функций
![]() существует криволинейный интеграл
второго рода по кривой
существует криволинейный интеграл
второго рода по кривой![]() в направлении возрастания параметра
в направлении возрастания параметра![]() (от
начальной точки кривой к конечной
точке), если существует
(от
начальной точки кривой к конечной
точке), если существует![]() ,
не зависящий от
,
не зависящий от![]() ,
т.е.
,
т.е.

Этой интеграл имеет следующее обозначение
![]() .
.
Он зависит от ориентации кривой
![]() .
.
В случае замкнутой кривой различают положительную и отрицательную ориентацию: против часовой стрелки и по часовой стрелке.
Этот случай подчеркивают следующим обозначением
![]() .
.
Функции
![]() в записи интеграла можно считать
координатами вектора
в записи интеграла можно считать
координатами вектора![]() .
Его называют векторным полем, заданным
на кривой
.
Его называют векторным полем, заданным
на кривой![]() .
.
Обозначим

Криволинейный
интеграл
![]() определяет работу векторного (силового)
поля
определяет работу векторного (силового)
поля![]() вдоль кривой
вдоль кривой![]() в направление от точки А к точке В. Работу
по замкнутой кривой часто называют
циркуляцией.
в направление от точки А к точке В. Работу
по замкнутой кривой часто называют
циркуляцией.
2. Формула Грина
Теорема
(Формула Грина). Пусть
в односвязной области
![]() задано векторное поле
задано векторное поле![]() таким, что функции
таким, что функции - непрерывные в Е. Кривая
- непрерывные в Е. Кривая![]() ,
множество
,
множество![]() ,
ограниченное этой кривой, выпуклое .
Тогда справедлива формула
,
ограниченное этой кривой, выпуклое .
Тогда справедлива формула
 .
.
Здесь
кривая
![]() обходится в положительном направлении
(против часовой стрелки).
обходится в положительном направлении
(против часовой стрелки).
Доказательство. Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.
 y
y
y = y2(x)
D
A
C
B
y= y1(x)
0 x1 x2 x
Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде:
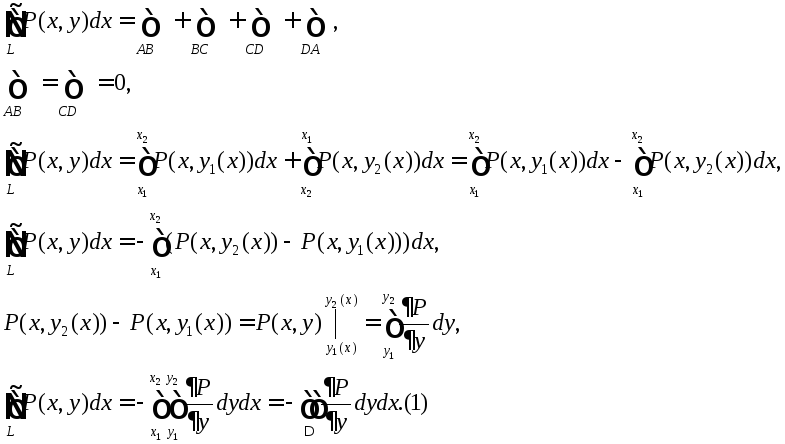
Рассуждая
аналогично, для области правильной при
проектировании на ось
![]() ,
получим
,
получим
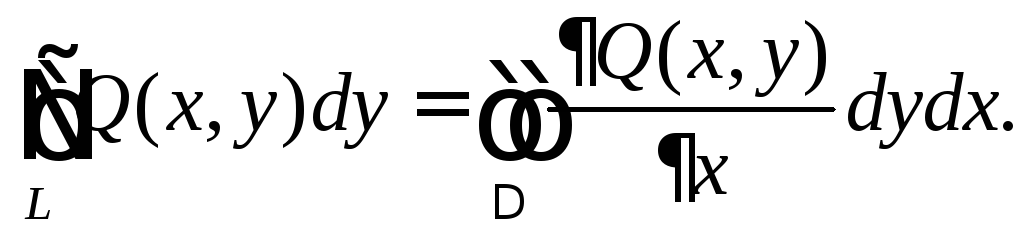 (2)
(2)
Складывая (1) и (2), получим формулу Грина.
3. Условия независимости интеграла от пути в r2
Лемма. Работа векторного поля не зависит от пути тогда и только тогда, когда любая циркуляция равна 0.
Доказательство.
Пусть
![]() произвольный замкнутый контур, точки
А и В – любые точки на
произвольный замкнутый контур, точки
А и В – любые точки на![]() .
Тогда
.
Тогда
![]() .
.
Работа
векторного поля не зависит от пути
![]() .
.
Лемма доказана.
Векторное
поле
![]() называется потенциальным, если существует
функция 2-х переменных
называется потенциальным, если существует
функция 2-х переменных![]() - скалярное поле такое, что
- скалярное поле такое, что ,
т.е
,
т.е .
.
Замечание.
В
дифференциальных уравнениях уравнение
первого порядка, записанное в дифференциалах
![]() ,
называется уравнением в полных
дифференциалах, если существует скалярное
поле
,
называется уравнением в полных
дифференциалах, если существует скалярное
поле![]() :
:![]() .
.
В
этом случае общий интеграл уравнения
имеет вид
![]()
Теорема.
Если в
односвязной области
![]() функции
функции
 непрерывны, то следующие условия
эквивалентны:
непрерывны, то следующие условия
эквивалентны:
поле
 - потенциальное в
- потенциальное в ;
;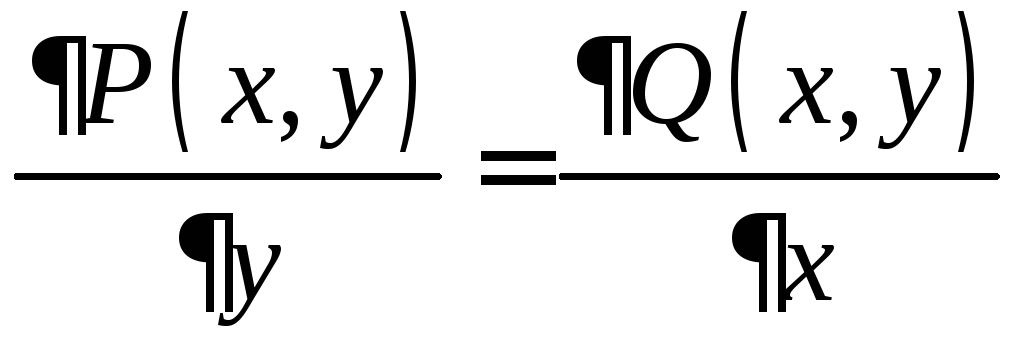 в
в
 ;
;Работа поля
 в
в не зависит от пути.
не зависит от пути.
Доказательство.
Будем
следовать схеме
![]() .
.
Поле
![]() - потенциальное в
- потенциальное в![]() ,
поэтому
,
поэтому![]()
![]() -скалярное
поле:
-скалярное
поле: ,
т.е.
,
т.е.
 .
.
Достаточно
проверить, что любая циркуляция в
![]() равна 0.
равна 0.
Используем формулу Грина, получим
 .
.
Покажем, что следующее скалярное поле и есть искомый потенциал:

Итак,

![]() .
Аналогично доказывается другое равенство.
Отсюда
.
Аналогично доказывается другое равенство.
Отсюда
![]()
![]() -
потенциальное поле в
-
потенциальное поле в
![]() .
.
Лекция 17 Площадь поверхности в r3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
