
- •Иванов в.И.
- •Лекция 1 Два определения интеграла Римана по прямоугольнику. Критерий Коши
- •1. Два определения интеграла Римана по прямоугольнику
- •2. Критерий Коши
- •2. Колебание функции по прямоугольнику и в точке. Критерий непрерывности функции в точке
- •3. Замкнутость множества точек, в которых колебание функции не меньше заданного положительного числа
- •1. Измеримость множества по Жордану в r2. Критерий измеримости
- •2.Достаточное условие измеримости
- •3. Определение двойного интеграла Римана по измеримой по Жордану области. Достаточное условие интегрируемости
- •Лекция 6
- •Лекция 8
- •2. Ортогональные криволинейные координаты. Якобиан в случае ортогональных координат
- •2. Сферические координаты в Rn. Их ортогональность
- •2. Сходимость кратных интегралов
- •3. Кратные несобственные интегралы 2-го рода. Абсолютная сходимость.
- •4. Сходимость кратных интегралов
- •2. Приложения криволинейного интеграла 1-го рода
- •Лекция 16 Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в r2
- •1. Криволинейный интеграл 2-го рода. Его физический смысл
- •2. Формула Грина
- •3. Условия независимости интеграла от пути в r2
- •Лекция 17 Площадь поверхности в r3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
- •1. Площадь поверхности в r3
- •2. Поверхностный интеграл 1-го рода. Его свойства, вычисление
- •2. Связь поверхностного интеграла 2-го рода с интегралом 1-го рода
- •Лекция 20 Скалярное и векторное поля. Поток, дивергенция, циркуляция и ротор векторного поля. Векторные линии и векторные трубки
- •1. Скалярное и векторное поля
- •2. Поток, дивергенция, циркуляция и ротор векторного поля
- •3. Векторные линии и векторные трубки
- •Лекция 21
- •Лекция 23 Дифференциальные формы. Замена переменных в дифференциальной форме. Дифференциал от дифференциальной формы. Второй дифференциал. Замкнутые и точные дифференциальные формы
- •1. Дифференциальные формы. Замена переменных в дифференциальной форме
- •2. Дифференциал от дифференциальной формы. Второй дифференциал
- •2. Площадь поверхности сферы в Rn
- •Лекция 25 Ориентация на поверхности и ее границе. Интегрирование дифференциальной формы по ориентированной поверхности
- •1. Ориентация на поверхности и ее границе
- •2. Интегрирование дифференциальной формы по ориентированной поверхности
Лекция 8
Формула
Дирихле-Лиувилля. Вычисление объема
![]() n-мерного
n-мерного
симплекса и шара
1. Формула Дирихле-Лиувилля
Пусть
 -n-мерный
симплекс,
-n-мерный
симплекс,
![]() ,
,
![]() -
интегрируема по Риману (несобственном
смысле),
-
интегрируема по Риману (несобственном
смысле),
![]() .
.
Рассмотрим кратный интеграл
![]() .
.
Справедлива следующая формула Дирихле-Лиувилля:

Здесь
![]() -
гамма-функция,
-
гамма-функция, .
.
Эта формула позволяет вычислить объемы некоторых тел.
2.
Вычисление объема
![]() n-мерного
симплекса и шара
n-мерного
симплекса и шара
Объем симплекса
 .
Имеем
.
Имеем

Объем октаэдра
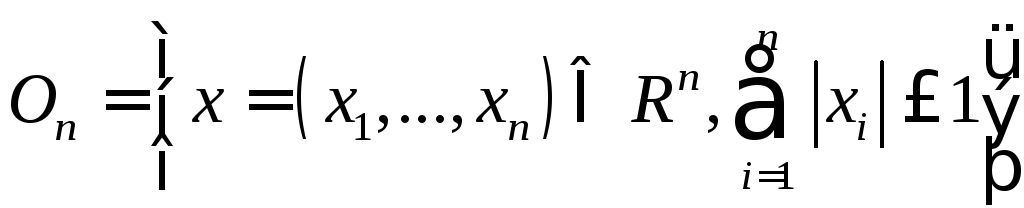 :
:
![]()

Объем шара
 :
:

Объем шара произвольного радиуса
 .
.
ЛЕКЦИЯ 9
Криволинейные координаты в Rn. Координатные линии и поверхности. Коэффициенты Ламе. Ортогональные криволинейные координаты. Якобиан в случае ортогональных координат. Формула замены переменных в кратном интеграле
1. Криволинейные координаты в Rn. Координатные линии и поверхности. Коэффициенты Ламе
Будем
говорить, что отображение
![]() определяет криволинейные координаты
определяет криволинейные координаты![]() в области
в области![]() ,
если:
,
если:
 -биекция
между
-биекция
между

 -гладкое
отображение, т.е
-гладкое
отображение, т.е
 или
или
Якобиан
 отображения
отображения
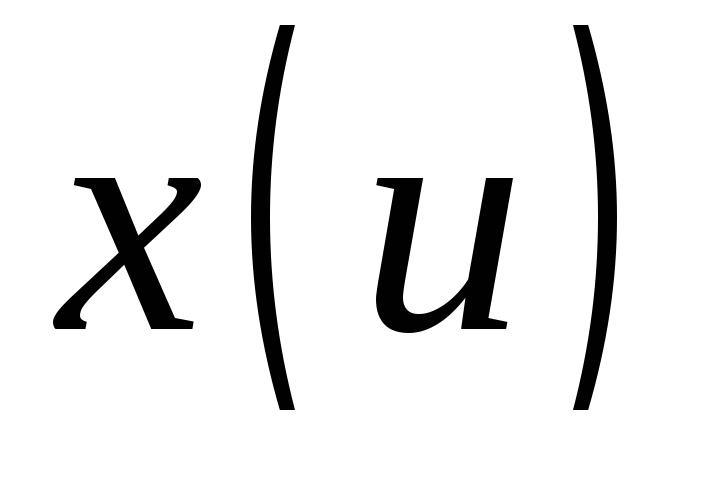 отличен от
0.
отличен от
0.
Здесь
 ,
,
![]() .
.
Если
в отображении
 зафиксируем все переменные
зафиксируем все переменные![]() кроме одной, то получим параметрическое
уравнение кривой, называемое координатной
линией. Если фиксируем все переменные
кроме одной, то получим параметрическое
уравнение кривой, называемое координатной
линией. Если фиксируем все переменные![]() кроме двух, то получим координатную
поверхность размерности 2 и т.д.
кроме двух, то получим координатную
поверхность размерности 2 и т.д.
Касательные векторы к координатным линиям имеют вид:

Модули этих векторов называются коэффициентами Ламе
![]() .
.
В якобиане касательные векторы стоят по столбцам, поэтому геометрический смысл модуля Якобиана - объем параллелепипеда, натянутого на касательные векторы.
2. Ортогональные криволинейные координаты. Якобиан в случае ортогональных координат
Криволинейная
система координаты
![]() называется ортогональной, если для
называется ортогональной, если для![]() :
:![]() .
.
В
случае ортогональных координат модуль
Якобиана
![]() .
.
3. Формула замены переменных в кратном интеграле
Теорема
(о замене переменных в кратном интеграле)
Если
![]() -компактные,
измеримые по Жордану множества в
-компактные,
измеримые по Жордану множества в![]() ,
,![]() - криволинейная система координат,
функция
- криволинейная система координат,
функция![]() , то
, то![]() и
и
![]() .
.
ЛЕКЦИЯ 10
Полярная система координат в R2. Двойной интеграл в полярных координатах. Цилиндрическая система координат в R3. Тройной интеграл в цилиндрических координатах
1. Полярная система координат в R2. Двойной интеграл в полярных координатах
Связь полярных координат с декартовыми имеет вид:
 .
.
Найдем касательные векторы и коэффициенты Ламе:

Полярные координаты – ортогональные:
![]() .
.
Область называется правильной областью в полярной системе координат, если ее можно записать системой неравенств
 .
.
В этом случае формула замены переменных выглядит следующий образом:
 .
.
2. Цилиндрическая система координат в R3. Тройной интеграл в цилиндрических координатах
Цилиндрические
координаты являются обобщением полярных
координат. Точка задается полярными
координатами
![]() проекции на плоскость
проекции на плоскость
![]() и координатой
и координатой
![]() по оси
по оси
![]() .
.
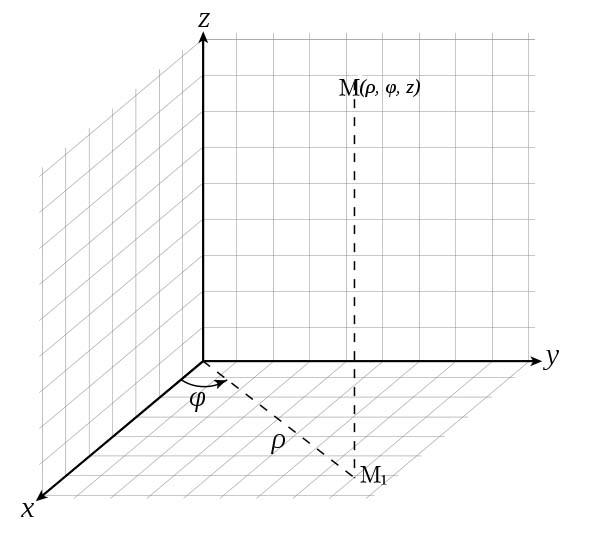
Название
координат связано с тем, что уравнение
прямого кругового цилиндра в них имеет
наиболее простое уравнение
![]() .
.
Соответствующее отображение имеет вид:
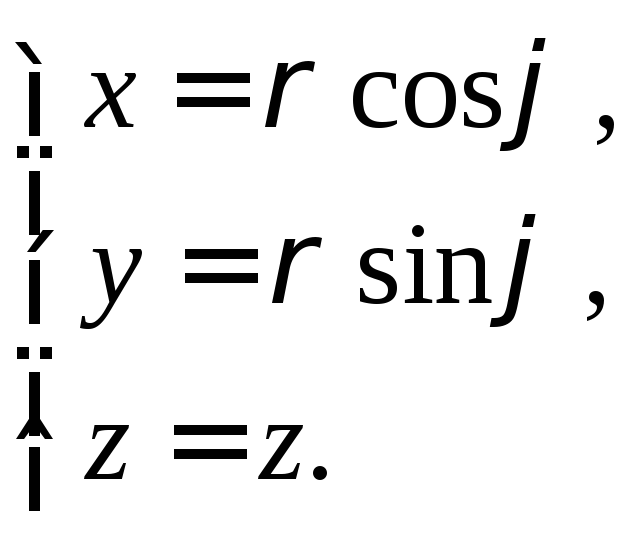
Якобиан для них такой же, как и для полярных координат:
 .
.
В этом случае формула замены переменных выглядит следующим образом:
![]() .
.
ЛЕКЦИЯ 11
Сферическая
система координат в R3.
Тройной интеграл в сферических
координатах. Сферические координаты в
Rn.
Их ортогональность.
Вычисление
объема
![]() n-мерного
шара
n-мерного
шара
1. Сферическая система координат в R3. Тройной интеграл
в сферических координатах
В
сферической системе координат точка
![]() задается тройкой
задается тройкой
![]() ,
где
,
где
![]() - расстояние от точки до начала координат,
- расстояние от точки до начала координат,
![]() - полярный угол проекции точки на
плоскость
- полярный угол проекции точки на
плоскость
![]() (иначе говоря, угол
(иначе говоря, угол
![]() ,
где
,
где
![]() - проекция точки
- проекция точки
![]() ),
),
![]() - угол между
- угол между
![]() и
и
![]() .
.

Название
связано с тем, что у точек на сфере с
центром в начале координат
![]() .
.
Формулы перехода имеют вид:

Найдем касательныу векторы, коэффициенты Ламе и убедимся в ортогональности сферических координат:
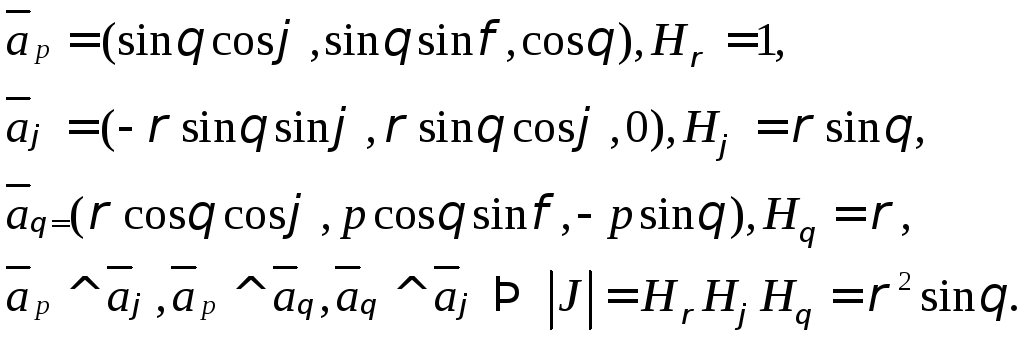
Сферические
координаты обычно используют только в
случае, когда тело
![]() в сферических координат имеет следующее
описание:
в сферических координат имеет следующее
описание:
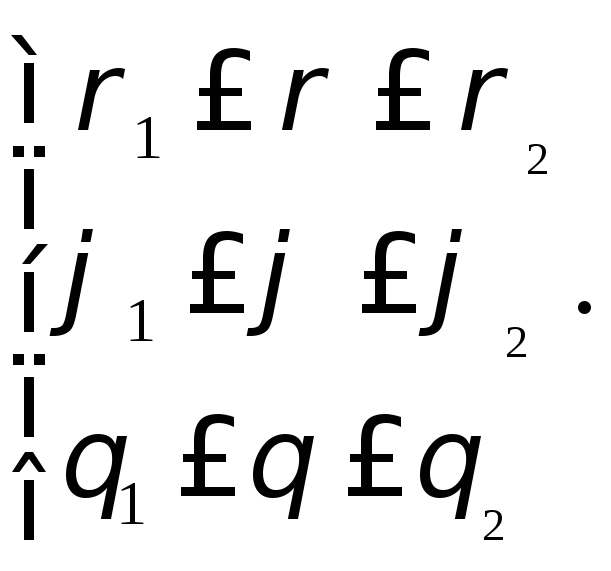
В этом случае формула замены переменных выглядит следующим образом:

