2.Достаточное условие измеримости

Достаточным условием измеримости по Жордану является гладкость границы множества (гладкость кривой, ограничивающей множество).

3. Определение двойного интеграла Римана по измеримой по Жордану области. Достаточное условие интегрируемости

Пусть ограниченное множество, А- прямоугольник,

-ограниченная функция,

.

Определение. Функция , если. При этом.

Можно показать, что это определение корректное, т.е. не зависит от выбора прямоугольника А.

Отметим, в частности, что по этому определению .

Теорема. (Достаточное условие интегрируемости по Риману). Если и Е измеримо по Жордану, то функция.

Доказательство. Достаточно доказать следующее включение

.

Пусть , Е измеримо по Жордану, т.е..

Пусть - точка непрерывности функции,, т.е существует окрестность:.

Отсюда следует, что - точка непрерывности функции.

Пусть, т.е существует окрестность:. Это также точка непрерывности.

Искомое включение доказано. Теорема доказана.

Лекция 6

Свойства двойного интеграла Римана. Теорема о среднем

1. Свойства двойного интеграла Римана

Будем предполагать, что все множества является измеримыми по Жордану.

Отметим следующие свойства интеграла Римана.

1. Если

(линейность интеграла Римана по функциям).

2. Если .

3. Если , то

(линейность интеграла Римана по множествам).

Доказательство.

,

, .

Имеем .

Отсюда .

4. Если .

5. Если , тои

Следует из неравенств .

6. Если , то.

Следует из неравенств

7. Если ,ограничена на Е, то

Следует из неравенств

2. Теорема о среднем

Теорема. Если Е компактное и связное множество в ,, то существует точка:.

Доказательство. Из непрерывности и компактности вытекает, что существуют точки .

Из свойства 6 следует, что . Если

.

По теореме о промежуточных значениях из непрерывности и связности Е следует, что существует точка:.

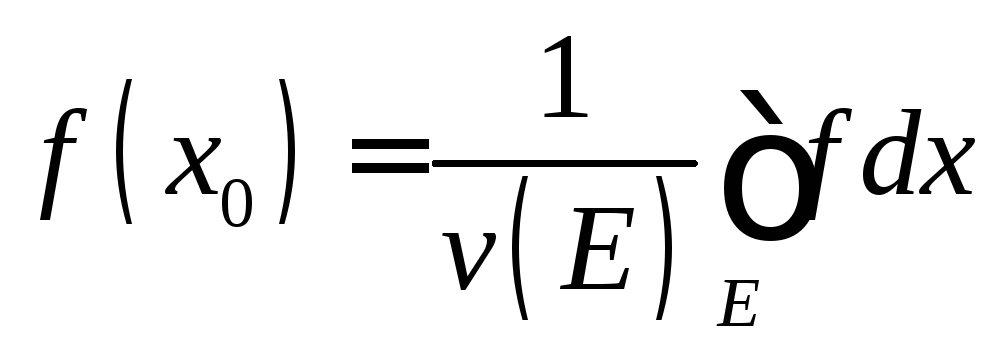Теорема доказана.

Если , то число называется средним значением функции на множестве .

ЛЕКЦИЯ 7

Определение кратного интеграла по параллелепипеду и по измеримой по Жордану области. Мера Жордана. Теорема Фубини. Вычисление кратного интеграла путем сведения к повторному

1. Определение кратного интеграла по параллелепипеду и по измеримой по Жордану области. Мера Жордана

Определение кратного интеграла Римана по параллелепипеду, меры Жордана, измеримой области по Жорану, интеграла Римана по произвольной измеримой по Жордану области дословно переносится с двумерного случая на общий -мерный случай.

2. Теорема Фубини

Пусть - параллелепипед в,

- параллелепипед в ,

- параллелепипед в , ,

Можно рассматривать интегралы

, ,.

Теорема Фубини. Если , то для любого,и справедливы следующие равенства

.

Последние два интеграла называют повторными.

3. Вычисление кратного интеграла путем сведения к повторному

Применим теорему Фубини к вычислению двойного интеграла по произвольной области.

Пусть ,. Такая область называется правильной при проектировании на осьАналогично, областьназывается правильной при проектировании на ось.

С помощью теоремы Фубини сведем вычисление двойного интеграла по правильной области при проектировании на ось к повторному интегралу. Пусть,

По определению интеграла и теореме Фубини

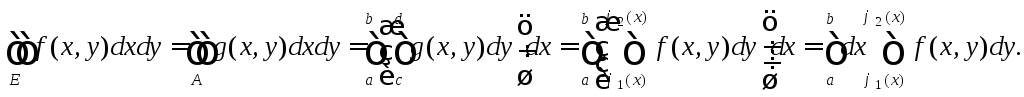
В случае тройного интеграла правильная область (цилиндрическое тело) при проектировании на плоскость записывается так:

.

Если , то применение теоремы Фубини сводит вычисление тройного интеграла к следующему повторному интегралу: