
- •Иванов в.И.
- •Лекция 1 Два определения интеграла Римана по прямоугольнику. Критерий Коши
- •1. Два определения интеграла Римана по прямоугольнику
- •2. Критерий Коши
- •2. Колебание функции по прямоугольнику и в точке. Критерий непрерывности функции в точке
- •3. Замкнутость множества точек, в которых колебание функции не меньше заданного положительного числа
- •1. Измеримость множества по Жордану в r2. Критерий измеримости
- •2.Достаточное условие измеримости
- •3. Определение двойного интеграла Римана по измеримой по Жордану области. Достаточное условие интегрируемости
- •Лекция 6
- •Лекция 8
- •2. Ортогональные криволинейные координаты. Якобиан в случае ортогональных координат
- •2. Сферические координаты в Rn. Их ортогональность
- •2. Сходимость кратных интегралов
- •3. Кратные несобственные интегралы 2-го рода. Абсолютная сходимость.
- •4. Сходимость кратных интегралов
- •2. Приложения криволинейного интеграла 1-го рода
- •Лекция 16 Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в r2
- •1. Криволинейный интеграл 2-го рода. Его физический смысл
- •2. Формула Грина
- •3. Условия независимости интеграла от пути в r2
- •Лекция 17 Площадь поверхности в r3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
- •1. Площадь поверхности в r3
- •2. Поверхностный интеграл 1-го рода. Его свойства, вычисление
- •2. Связь поверхностного интеграла 2-го рода с интегралом 1-го рода
- •Лекция 20 Скалярное и векторное поля. Поток, дивергенция, циркуляция и ротор векторного поля. Векторные линии и векторные трубки
- •1. Скалярное и векторное поля
- •2. Поток, дивергенция, циркуляция и ротор векторного поля
- •3. Векторные линии и векторные трубки
- •Лекция 21
- •Лекция 23 Дифференциальные формы. Замена переменных в дифференциальной форме. Дифференциал от дифференциальной формы. Второй дифференциал. Замкнутые и точные дифференциальные формы
- •1. Дифференциальные формы. Замена переменных в дифференциальной форме
- •2. Дифференциал от дифференциальной формы. Второй дифференциал
- •2. Площадь поверхности сферы в Rn
- •Лекция 25 Ориентация на поверхности и ее границе. Интегрирование дифференциальной формы по ориентированной поверхности
- •1. Ориентация на поверхности и ее границе
- •2. Интегрирование дифференциальной формы по ориентированной поверхности
3. Замкнутость множества точек, в которых колебание функции не меньше заданного положительного числа
Лемма
4.![]() множество
множество
![]() -
ограниченное и замкнутое, т.е. компактное.
-
ограниченное и замкнутое, т.е. компактное.
Доказательство.
Так как
![]() ,
то
,
то
![]() -
ограниченное.
-
ограниченное.
Пусть
![]() - предельная точка
- предельная точка![]() .
Покажем, что она принадлежит
.
Покажем, что она принадлежит![]() .
Поскольку
.
Поскольку![]() предельная точка, то существует
последовательность
предельная точка, то существует
последовательность![]() ,
сходящая к
,
сходящая к![]() .
Отсюда для любого
.
Отсюда для любого![]() найдется
найдется![]() ,
,![]() открытое, поэтому существует
открытое, поэтому существует![]() такое, что
такое, что![]() .
Отсюда имеем
.
Отсюда имеем![]() ,
то есть
,
то есть
![]() .
.
Лемма доказана.
4. Описание множества точек разрыва функции
Пусть
![]() -
множество точек разрыва функции
-
множество точек разрыва функции![]() на прямоугольнике А.
на прямоугольнике А.
Лемма
5.
 .
.
Множество,
которое можно представить в виде счетного
объединения замкнутых множеств называется
множеством типа
![]() .
Итак,
.
Итак,
множество
точек разрыва функции
![]() -
множество типа
-
множество типа![]() .
.
ЛЕКЦИЯ 4
Критерий Лебега интегрируемости по прямоугольнику
1. Критерий Лебега интегрируемости по прямоугольнику
Теорема
1. (Критерий
Лебега).
Ограниченная
функция ![]() тогда и только
тогда, когда
тогда и только
тогда, когда
![]() .
.
Следствие. Всякая функция, имеющая не более чем счетное множество точек разрыва интегрируемая.
Теорема
2. (Критерий
интегрируемости). Ограниченная функция
![]() тогда и только
тогда, когда для любого
тогда и только
тогда, когда для любого
![]() .
.![]() .
.
Сначала
![]() выведем
теорему 1 из теоремы 2.Доказательство
теоремы 1.
выведем
теорему 1 из теоремы 2.Доказательство
теоремы 1.
Необходимость.Ограниченная функция![]() по теореме 2, если для любого
по теореме 2, если для любого![]() .
. .
.
Достаточность.
![]()
По
теореме 2 имеем ![]() .
.
Теорема доказана.
Доказательство теоремы 2.
Необходимость
. Предположим,
что существует
![]() ,
,![]() .
То есть найдется
.
То есть найдется![]() такое, что для любого набора
такое, что для любого набора![]() ,
, ,
но
,
но .
Рассмотрим любое разбиение Т прямоугольника
А на прямоугольники
.
Рассмотрим любое разбиение Т прямоугольника
А на прямоугольники![]() .
Пусть
.
Пусть![]() -множество
всех тех прямоугольников
-множество
всех тех прямоугольников![]() ,
внутри которых находится хотя бы одна
точка множества
,
внутри которых находится хотя бы одна
точка множества![]()
![]() .
Заметим что для любого прямоугольника
из
.
Заметим что для любого прямоугольника
из![]() колебание функции на этом прямоугольнике
не меньше чем
колебание функции на этом прямоугольнике
не меньше чем![]() .
Отсюда для любого разбиения Т
.
Отсюда для любого разбиения Т![]() Это означает, что функция не интегрируема
на прямоугольнике. Получили противоречие.
Значит, для любого
Это означает, что функция не интегрируема
на прямоугольнике. Получили противоречие.
Значит, для любого![]()
![]() .
.
Достаточность.
Положим
![]() .
.
Так
как
![]() ,
то его можно покрыть открытыми
прямоугольниками
,
то его можно покрыть открытыми
прямоугольниками![]() ,
, .
Выделим из
.
Выделим из![]() конечное подпокрытие
конечное подпокрытие![]() .
Рассмотрим
.
Рассмотрим![]() .
Оно является компактом. Для любого
.
Оно является компактом. Для любого![]() ,
,![]() .Из
определения
.Из
определения![]() получим,
что существует открытый квадратP
такой, что колебание функции на нем
меньше чем
получим,
что существует открытый квадратP
такой, что колебание функции на нем
меньше чем
![]() .
КвадратыP
образуют открытое покрытие множества
К. Выделим из него конечное покрытие
II.
Продолжим стороны прямоугольников,
составляющих I
и II
до пересечения со сторонами прямоугольника
А. Получим разбиение Т, для которого
.
КвадратыP
образуют открытое покрытие множества
К. Выделим из него конечное покрытие
II.
Продолжим стороны прямоугольников,
составляющих I
и II
до пересечения со сторонами прямоугольника
А. Получим разбиение Т, для которого
![]() .
.
Таким
образом, ![]() .
.
Теорема доказана.
Следствия из критерия Лебега.
 .
. .
.Пусть
 .
Тогда
.
Тогда .
.
ЛЕКЦИЯ 5
Измеримость множества по Жордану в R2. Критерий измеримости. Достаточное условие измеримости. Определение двойного интеграла Римана по измеримой по Жордану области. Достаточное условие интегрируемости
1. Измеримость множества по Жордану в r2. Критерий измеримости
Пусть
![]() - ограниченное множество, А- прямоугольник,
- ограниченное множество, А- прямоугольник,
![]() ,
,
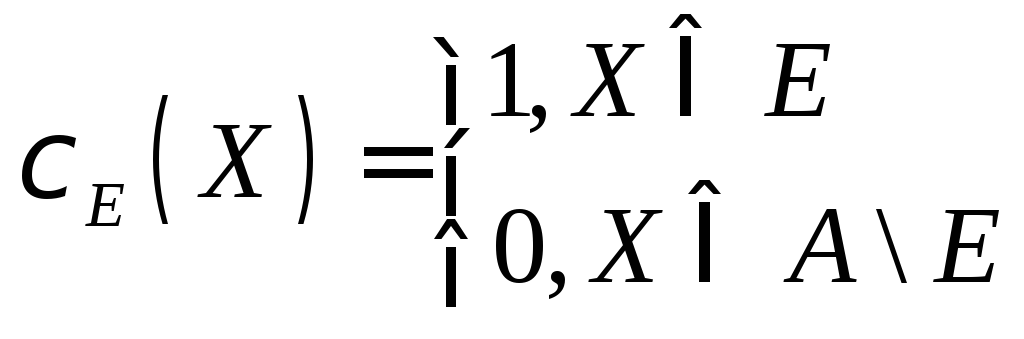 -
характеристическая
функция
множества E.
-
характеристическая
функция
множества E.
Определение.
Множество
Е измеримо по Жордану или имеет объем
![]() ,
если
,
если![]() ,
при этом
,
при этом![]() .
.
Это определение на самом деле не зависит от выбора прямоугольника А и в этом смысле является корректным.
Пусть
![]() -
множество всех внутренних точек множества
Е,
-
множество всех внутренних точек множества
Е,
![]() -
внешность множества Е или внутренность
дополнения множества Е,
-
внешность множества Е или внутренность
дополнения множества Е,
![]() -граница
множества Е.
-граница
множества Е.
Теорема.
(Критерий измеримости по Жордану). Е
измеримо по Жордану тогда и только
тогда, когда
![]()
Доказательство.
Е измеримо
по Жордану
![]()
![]()
![]()
![]() .
.
Докажем
равенство
![]() ,
т.е. что множество точек разрывахарактеристической
функции совпадает с границей множества.
,
т.е. что множество точек разрывахарактеристической
функции совпадает с границей множества.
Рассмотрим три случая для точек прямоугольника А
Точка
 .
Тогда существует окрестность
.
Тогда существует окрестность такая, что
такая, что .
.Точка
 существует окрестность
существует окрестность такая, что
такая, что
![]() .
.
Точка

![]() .
.
