
- •Иванов в.И.
- •Лекция 1 Два определения интеграла Римана по прямоугольнику. Критерий Коши
- •1. Два определения интеграла Римана по прямоугольнику
- •2. Критерий Коши
- •2. Колебание функции по прямоугольнику и в точке. Критерий непрерывности функции в точке
- •3. Замкнутость множества точек, в которых колебание функции не меньше заданного положительного числа
- •1. Измеримость множества по Жордану в r2. Критерий измеримости
- •2.Достаточное условие измеримости
- •3. Определение двойного интеграла Римана по измеримой по Жордану области. Достаточное условие интегрируемости
- •Лекция 6
- •Лекция 8
- •2. Ортогональные криволинейные координаты. Якобиан в случае ортогональных координат
- •2. Сферические координаты в Rn. Их ортогональность
- •2. Сходимость кратных интегралов
- •3. Кратные несобственные интегралы 2-го рода. Абсолютная сходимость.
- •4. Сходимость кратных интегралов
- •2. Приложения криволинейного интеграла 1-го рода
- •Лекция 16 Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в r2
- •1. Криволинейный интеграл 2-го рода. Его физический смысл
- •2. Формула Грина
- •3. Условия независимости интеграла от пути в r2
- •Лекция 17 Площадь поверхности в r3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
- •1. Площадь поверхности в r3
- •2. Поверхностный интеграл 1-го рода. Его свойства, вычисление
- •2. Связь поверхностного интеграла 2-го рода с интегралом 1-го рода
- •Лекция 20 Скалярное и векторное поля. Поток, дивергенция, циркуляция и ротор векторного поля. Векторные линии и векторные трубки
- •1. Скалярное и векторное поля
- •2. Поток, дивергенция, циркуляция и ротор векторного поля
- •3. Векторные линии и векторные трубки
- •Лекция 21
- •Лекция 23 Дифференциальные формы. Замена переменных в дифференциальной форме. Дифференциал от дифференциальной формы. Второй дифференциал. Замкнутые и точные дифференциальные формы
- •1. Дифференциальные формы. Замена переменных в дифференциальной форме
- •2. Дифференциал от дифференциальной формы. Второй дифференциал
- •2. Площадь поверхности сферы в Rn
- •Лекция 25 Ориентация на поверхности и ее границе. Интегрирование дифференциальной формы по ориентированной поверхности
- •1. Ориентация на поверхности и ее границе
- •2. Интегрирование дифференциальной формы по ориентированной поверхности
Лекция 23 Дифференциальные формы. Замена переменных в дифференциальной форме. Дифференциал от дифференциальной формы. Второй дифференциал. Замкнутые и точные дифференциальные формы
1. Дифференциальные формы. Замена переменных в дифференциальной форме
Пусть
![]() открытое множество, точка
открытое множество, точка
![]() ,
,
![]() .
.
Определение.
Дифференциальной формой
![]() порядкаk
в области
порядкаk
в области
![]() называется выражение:
называется выражение:
![]()
где
функции
![]() - гладкие,
- гладкие,![]() -
внешнее произведение (операция),
обладающее свойствами:
-
внешнее произведение (операция),
обладающее свойствами:
1)
![]() - ассоциативность;
- ассоциативность;
2)
![]() -антисимметричность;
-антисимметричность;
3)
![]()
![]() некоторые функции – полилинейность.
некоторые функции – полилинейность.
Определим
замену переменных в дифференциальной
форме. Пусть
![]() - дифференциальная форма порядкаk
в пространстве
- дифференциальная форма порядкаk
в пространстве
![]() ,
,![]() ,
,![]() ,
открытое - замена переменных, т.е.
,
открытое - замена переменных, т.е.

Дифференциалы этих функций имеет вид:

Замена
переменных
![]() в дифференциальной форме
в дифференциальной форме![]() порядкаk
в пространстве
порядкаk
в пространстве
![]() определяет новую дифференциальную
форму
определяет новую дифференциальную
форму![]() порядкаk
в пространстве
порядкаk
в пространстве
![]() по правилу:
по правилу:
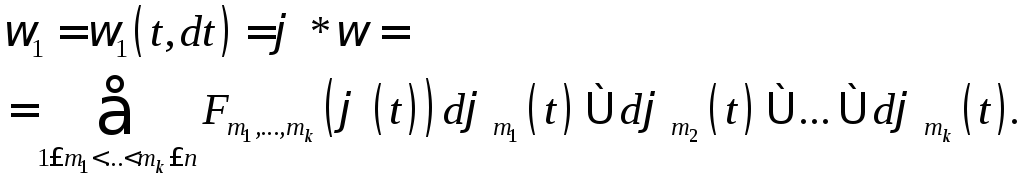
2. Дифференциал от дифференциальной формы. Второй дифференциал
Пусть
![]() -
дифференциальная форма порядкаk
в
-
дифференциальная форма порядкаk
в
![]() .
.
Дифференциалом
![]() дифференциальной формы
дифференциальной формы![]() порядкаk
в
порядкаk
в
![]() называется новая дифференциальная
форма порядкаk+1
в
называется новая дифференциальная
форма порядкаk+1
в
![]() ,
получаемая по правилу:
,
получаемая по правилу:

Теорема.
Для любой формы
![]()
![]() .
.
Доказательство. Достаточно доказать для формы вида
![]() .
.
Имеем

Рассмотрим следующие случаи:
1)
если
![]() соответствующие слагаемые =0;
соответствующие слагаемые =0;
2)
если
![]() в
в![]() есть два слагаемых
есть два слагаемых ,
сумма которых =0. Теорема доказана.
,
сумма которых =0. Теорема доказана.
3. Замкнутые и точные дифференциальные формы
Дифференциальная
форма
![]() называется замкнутой в области
называется замкнутой в области![]() ,
если
,
если![]() вU.
вU.
Дифференциальная
форма
![]() называется точной в области
называется точной в области![]() ,
если
,
если![]() .
.
Лемма. Всякая точная форма является замкнутой.
Доказательство
вытекает из того, что
![]() - замкнутая форма.
- замкнутая форма.
Теорема
Пуанкаре.
Если ![]() - гладкая форма и
U
– односвязная область, то всякая
замкнутая форма является точной.
- гладкая форма и
U
– односвязная область, то всякая
замкнутая форма является точной.
ЛЕКЦИЯ 24
![]() -мерные
гладкие поверхности в Rn.
Площадь поверхности. Площадь поверхности
сферы в Rn
-мерные
гладкие поверхности в Rn.
Площадь поверхности. Площадь поверхности
сферы в Rn
1.
![]() -мерные
гладкие поверхности вRn.
Площадь поверхности
-мерные
гладкие поверхности вRn.
Площадь поверхности
Определение.
![]() -мерная
поверхностьS
в
-мерная
поверхностьS
в
![]() задается параметрически при помощи
задается параметрически при помощи![]() параметров следующим образом:
параметров следующим образом:


Если
![]()
![]() -мерная
поверхность в
-мерная
поверхность в![]() .
.![]() -
дифференциальная форма порядкаk
в
-
дифференциальная форма порядкаk
в
![]() ,
то ее сужение наS
есть новая дифференциальная форма
,
то ее сужение наS
есть новая дифференциальная форма
![]() порядкаk
в
порядкаk
в
![]() ,
определенная по правилу:
,
определенная по правилу:
Пусть
![]() ,
,
![]() -
k-мерная
поверхность в
-
k-мерная
поверхность в
![]() ,
,![]() .
.
Пусть
![]() - множество изk
векторов в
- множество изk
векторов в
![]() .
.
![]() -
объем параллелепипеда, натянутого на
эти k
векторов.
-
объем параллелепипеда, натянутого на
эти k
векторов.
Этой объем можно определить по индукции:

Пусть
матрица порядка
![]() имеет вид
имеет вид![]() .
Эта симметричная матрица называется
матрицей Грама. Её определитель обозначим
.
Эта симметричная матрица называется
матрицей Грама. Её определитель обозначим
![]() .
.
Отметим некоторые свойства определителя Грама:
1.![]() ,
,
2.
![]() - линейны зависимы.
- линейны зависимы.
Отметим,
что

Теорема.
![]() .
.
Запишем
касательные векторы к поверхности
![]() :
:
 -
-
Определение.
Площадью
поверхности
![]() называется число
называется число .
.
Понятие
площади поверхности позволяет легко
определить поверхностный интеграл
первого рода. Пусть
![]() -
-![]() -мерная
поверхность в
-мерная
поверхность в![]() и задана функция
и задана функция![]() .
.
Определение.
Поверхностным
интегралом первого рода от функции
![]() по поверхности
по поверхности![]() называется число
называется число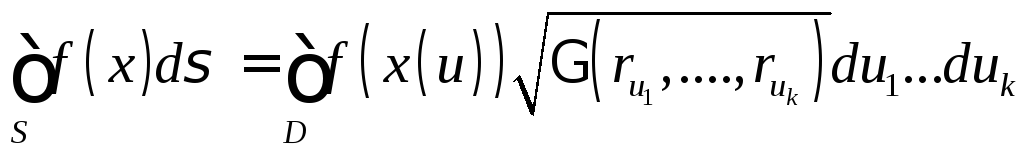 .
.
В
частности,
![]() .
.
Если
векторы
![]() - попарно ортогональны то
- попарно ортогональны то![]() .
.
2. Площадь поверхности сферы в Rn
Пусть
![]() - сфера радиуса
- сфера радиуса![]() .
Будем использовать ортогональную
сферическую систему координат для
параметрической записи сферы:
.
Будем использовать ортогональную
сферическую систему координат для
параметрической записи сферы:
![]() ,
,
![]()

Найдем касательные векторы и их длины:



………….

Отсюда
![]() .
.
Площадь поверхности сферы равна

