
- •Иванов в.И.
- •Лекция 1 Два определения интеграла Римана по прямоугольнику. Критерий Коши
- •1. Два определения интеграла Римана по прямоугольнику
- •2. Критерий Коши
- •2. Колебание функции по прямоугольнику и в точке. Критерий непрерывности функции в точке
- •3. Замкнутость множества точек, в которых колебание функции не меньше заданного положительного числа
- •1. Измеримость множества по Жордану в r2. Критерий измеримости
- •2.Достаточное условие измеримости
- •3. Определение двойного интеграла Римана по измеримой по Жордану области. Достаточное условие интегрируемости
- •Лекция 6
- •Лекция 8
- •2. Ортогональные криволинейные координаты. Якобиан в случае ортогональных координат
- •2. Сферические координаты в Rn. Их ортогональность
- •2. Сходимость кратных интегралов
- •3. Кратные несобственные интегралы 2-го рода. Абсолютная сходимость.
- •4. Сходимость кратных интегралов
- •2. Приложения криволинейного интеграла 1-го рода
- •Лекция 16 Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в r2
- •1. Криволинейный интеграл 2-го рода. Его физический смысл
- •2. Формула Грина
- •3. Условия независимости интеграла от пути в r2
- •Лекция 17 Площадь поверхности в r3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
- •1. Площадь поверхности в r3
- •2. Поверхностный интеграл 1-го рода. Его свойства, вычисление
- •2. Связь поверхностного интеграла 2-го рода с интегралом 1-го рода
- •Лекция 20 Скалярное и векторное поля. Поток, дивергенция, циркуляция и ротор векторного поля. Векторные линии и векторные трубки
- •1. Скалярное и векторное поля
- •2. Поток, дивергенция, циркуляция и ротор векторного поля
- •3. Векторные линии и векторные трубки
- •Лекция 21
- •Лекция 23 Дифференциальные формы. Замена переменных в дифференциальной форме. Дифференциал от дифференциальной формы. Второй дифференциал. Замкнутые и точные дифференциальные формы
- •1. Дифференциальные формы. Замена переменных в дифференциальной форме
- •2. Дифференциал от дифференциальной формы. Второй дифференциал
- •2. Площадь поверхности сферы в Rn
- •Лекция 25 Ориентация на поверхности и ее границе. Интегрирование дифференциальной формы по ориентированной поверхности
- •1. Ориентация на поверхности и ее границе
- •2. Интегрирование дифференциальной формы по ориентированной поверхности
2. Связь поверхностного интеграла 2-го рода с интегралом 1-го рода
Имеем

Отсюда
![]() .
.
3. Теорема Гаусса-Остроградского
Пусть
![]() замкнутая поверхность с внешней нормалью
замкнутая поверхность с внешней нормалью![]() .
.![]() -
тело, ограниченное этой поверхностью,
-
тело, ограниченное этой поверхностью,![]() .
.
Тогда имеет место следующая теорема.
Теорема (теорема Гаусса - Остроградского). Справедливо равенство:

где
 -
дивергенция поля
-
дивергенция поля
![]() .
.
Доказательство.
Имеем
![]() ,
,
 .
.
Поэтому достаточно доказать следующие равенства:
 ,
,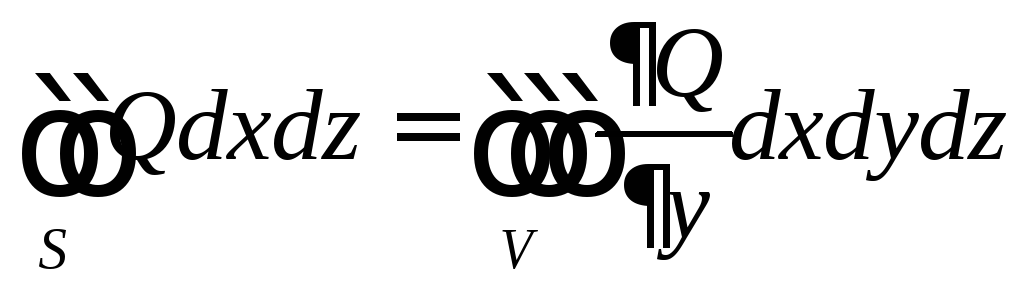 ,
, .
.
Пусть
![]() .
Тогда
.
Тогда

Далее


Аналогично
 ,
, .
.
Теорема доказана.
ЛЕКЦИЯ 19
Формула Стокса. Условия независимости криволинейного интеграла
2-го рода от пути в R3
1. Формула Стокса
Пусть![]()

![]() -
двусторонняя поверхность
-
двусторонняя поверхность
 .
.
Тогда
множество
![]() - граница (или край) поверхностиS.
Определим важное понятие ротора
векторного поля:
- граница (или край) поверхностиS.
Определим важное понятие ротора
векторного поля:
 ,
,
где
![]()
 - символический оператор из частных
производных, оператор « набла».
- символический оператор из частных
производных, оператор « набла».
Теорема
(Формула Стокса).
Если ориентации на
![]() и
и![]() согласованы, то
согласованы, то
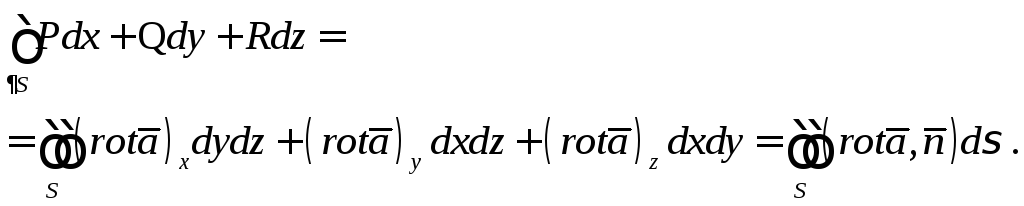
Доказательство. Необходимо доказать равенство:

или три равенства

Для простоты докажем первое равенство в предложении, что поверхность
![]() .
.
Имеем
![]()





![]()
![]()


Что и требовалось показать.
2. Условия независимости криволинейного интеграла
2-го рода от пути в R3
Векторное
поле
![]() называетсяпотенциальным,
если существует скалярное поле
называетсяпотенциальным,
если существует скалярное поле
![]() - потенциал такой, что
- потенциал такой, что или
или ,
,
т.е.
![]() есть решение системы
есть решение системы
Лемма.
Работа векторного поля
![]() в области
в области![]() не
зависит от пути, а зависит только от
начала и конца пути
не
зависит от пути, а зависит только от
начала и конца пути![]() любая
циркуляция вE
равна 0.
любая
циркуляция вE
равна 0.
Доказательство. Точно такое же, как в плоском случае.
Теорема. Следующие условия эквивалентны:
поле
 потенциальное, в односвязной областиE;
потенциальное, в односвязной областиE;ротор
 в областиE;
в областиE;работа поля
 вE
не зависит от пути.
вE
не зависит от пути.
Доказательство.
Будем следовать схеме
![]() .
.
![]() :
:
![]()
![]()
![]()
![]() .
.
![]() Имеем
Имеем


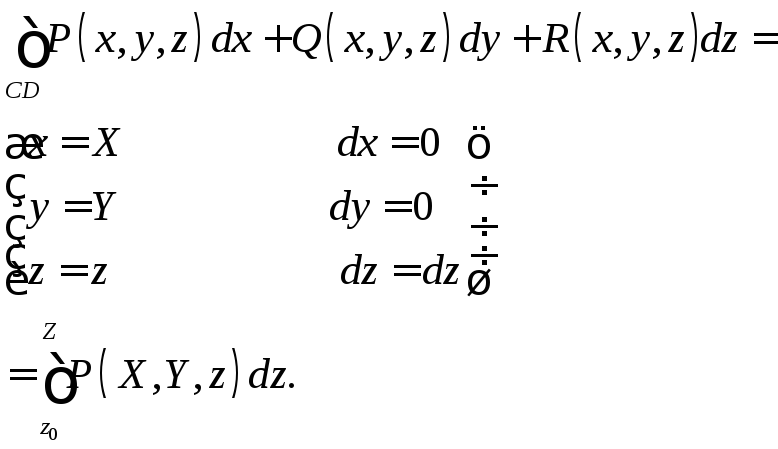
Отсюда
 .
Аналогично доказываются остальные
равенства.
.
Аналогично доказываются остальные
равенства.
Лекция 20 Скалярное и векторное поля. Поток, дивергенция, циркуляция и ротор векторного поля. Векторные линии и векторные трубки
1. Скалярное и векторное поля
Напомним определения, с которыми мы уже работали.
Если
в каждой точке
![]() некоторой области V пространства (или
плоскости) определена скалярная функция
u = u(M), то говорят, что в области V заданоскалярное
поле u =
u(M) = u(x,y,z).
некоторой области V пространства (или
плоскости) определена скалярная функция
u = u(M), то говорят, что в области V заданоскалярное
поле u =
u(M) = u(x,y,z).
Если в каждой точке M(x,y,z) некоторой области V пространства (или плоскости) определен вектор
![]()
то
говорят, что в области V задано
векторное
поле
![]() .
.
2. Поток, дивергенция, циркуляция и ротор векторного поля
Важнейшими характеристиками векторных полей являются поток, дивергенция, циркуляция и ротор векторного поля
Пусть
в каждой точке некоторой поверхности
S определен непрерывный вектор
![]() .
Зададим
направление нормали
.
Зададим
направление нормали![]() к поверхности S.
к поверхности S.
Напомним,
что поток векторного поля
![]() через поверхность
через поверхность![]() в направлении нормали
в направлении нормали![]() задается поверхностным интегралом 2-го
рода или поверхностным интегралом 1-го
рода:
задается поверхностным интегралом 2-го
рода или поверхностным интегралом 1-го
рода:
![]() .
.
Дивергенцией
(или расходимостью) дифференцируемого
векторного поля
![]() называется
скалярное поле
называется
скалярное поле
 .
.
Циркуляцией
векторного
поля
![]() вдоль замкнутой кривой L называется
криволинейный интеграл второго рода
вдоль замкнутой кривой L называется
криволинейный интеграл второго рода
![]()
В
случае, когда векторное поле
![]() является
силовым полем,циркуляция
даёт величину работы этого поля вдоль
кривой L.
Ротором
(или вихрем) дифференцируемого векторного
поля
является
силовым полем,циркуляция
даёт величину работы этого поля вдоль
кривой L.
Ротором
(или вихрем) дифференцируемого векторного
поля
![]() называется вектор
называется вектор
 .
.
Операторы grad, div, rot называются основными операторами теории поля.
