
- •Иванов в.И.
- •Лекция 1 Два определения интеграла Римана по прямоугольнику. Критерий Коши
- •1. Два определения интеграла Римана по прямоугольнику
- •2. Критерий Коши
- •2. Колебание функции по прямоугольнику и в точке. Критерий непрерывности функции в точке
- •3. Замкнутость множества точек, в которых колебание функции не меньше заданного положительного числа
- •1. Измеримость множества по Жордану в r2. Критерий измеримости
- •2.Достаточное условие измеримости
- •3. Определение двойного интеграла Римана по измеримой по Жордану области. Достаточное условие интегрируемости
- •Лекция 6
- •Лекция 8
- •2. Ортогональные криволинейные координаты. Якобиан в случае ортогональных координат
- •2. Сферические координаты в Rn. Их ортогональность
- •2. Сходимость кратных интегралов
- •3. Кратные несобственные интегралы 2-го рода. Абсолютная сходимость.
- •4. Сходимость кратных интегралов
- •2. Приложения криволинейного интеграла 1-го рода
- •Лекция 16 Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в r2
- •1. Криволинейный интеграл 2-го рода. Его физический смысл
- •2. Формула Грина
- •3. Условия независимости интеграла от пути в r2
- •Лекция 17 Площадь поверхности в r3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
- •1. Площадь поверхности в r3
- •2. Поверхностный интеграл 1-го рода. Его свойства, вычисление
- •2. Связь поверхностного интеграла 2-го рода с интегралом 1-го рода
- •Лекция 20 Скалярное и векторное поля. Поток, дивергенция, циркуляция и ротор векторного поля. Векторные линии и векторные трубки
- •1. Скалярное и векторное поля
- •2. Поток, дивергенция, циркуляция и ротор векторного поля
- •3. Векторные линии и векторные трубки
- •Лекция 21
- •Лекция 23 Дифференциальные формы. Замена переменных в дифференциальной форме. Дифференциал от дифференциальной формы. Второй дифференциал. Замкнутые и точные дифференциальные формы
- •1. Дифференциальные формы. Замена переменных в дифференциальной форме
- •2. Дифференциал от дифференциальной формы. Второй дифференциал
- •2. Площадь поверхности сферы в Rn
- •Лекция 25 Ориентация на поверхности и ее границе. Интегрирование дифференциальной формы по ориентированной поверхности
- •1. Ориентация на поверхности и ее границе
- •2. Интегрирование дифференциальной формы по ориентированной поверхности
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Тульский государственный университет»
Кафедра прикладной математики и информатики
Иванов в.И.
профессор, д.ф.-м.н.
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
Математический анализ
(Часть 4)
Направление подготовки: 010200 «Математика и компьютерные науки»
Профиль подготовки: «Математическое и компьютерное моделирование»
Направление подготовки: 010800 «Механика и математическое моделирование»
Профиль подготовки: «Общий профиль»
Форма обучения: очная
Тула 2013 г.
Рассмотрено на заседании кафедры
протокол № 1 от 02 сентября 2013 г.
Зав. кафедрой________________В.И. Иванов
СОДЕРЖАНИЕ
Тула 2013 г. 1
Лемма 4. множество - ограниченное и замкнутое, т.е. компактное. 10
Двойной интеграл позволяет вычислить массу, координаты центра тяжести, статичные моменты первого и второго порядка плоской пластинки, начиненной веществом. 32
и , 32
и . 33
53
- Формула Стокса. 63
5) , 63
ЛЕКЦИЯ 18. Поверхностный интеграл 2-го рода. Его связь с поверхностным интегралом 1-го рода. Теорема Гаусса-Остроградского 44
ЛЕКЦИЯ 19. Формула Стокса. Условия независимости криволинейного интеграла 2-го рода от пути вR3 47
ЛЕКЦИЯ 20 Скалярное и векторное поля. Поток, дивергенция, циркуляция и ротор векторного поля. Векторные линии и векторные трубки 49
ЛЕКЦИЯ 21. Потенциальные и соленоидальные векторные поля. Векторная интерпретация формул Стокса и Гаусса-Остроградского 51
ЛЕКЦИЯ 22. Дифференциальные векторные операции 2-го порядка. Гармоническое поле и уравнение Лапласа. Гармонические функции. Разложение векторного поля на сумму потенциального и соленоидального полей и уравнение Пуассона. Вторая формула Грина 52
ЛЕКЦИЯ 23. Дифференциальные формы. Замена переменных в дифференциальной форме. Дифференциал от дифференциальной формы. Второй дифференциал. Замкнутые и точные дифференциальные формы 54
ЛЕКЦИЯ
24.
![]() -мерные
гладкие поверхности в Rn.
Площадь поверхности. Площадь поверхности
сферы вRn 57
-мерные
гладкие поверхности в Rn.
Площадь поверхности. Площадь поверхности
сферы вRn 57
ЛЕКЦИЯ 25. Ориентация на поверхности и ее границе. Интегрирование дифференциальной формы по ориентированной поверхности 60
ЛЕКЦИЯ 26. Общая формула Стокса. Частные случаи общей формулы Стокса 61
Лекция 1 Два определения интеграла Римана по прямоугольнику. Критерий Коши
1. Два определения интеграла Римана по прямоугольнику
Пусть
![]()
![]() -параллелепипед
в
-параллелепипед
в![]() (замкнутый
параллелепипед с гранямипараллельными
координатным плоскостям),
(замкнутый
параллелепипед с гранямипараллельными
координатным плоскостям),
![]() -
объем параллелепипеда, функция
-
объем параллелепипеда, функция![]() -ограниченная.
-ограниченная.
Необходимо
определить число связанное с
![]() ,
называемое интегралом от
,
называемое интегралом от![]() по множеству
по множеству![]() :
:![]() .
.
Для
простоты все построения будем вести
для
![]() .
В этом случае
.
В этом случае
![]()
![]() ,
,
![]()
![]() .
.
Пусть
![]() ,
,
![]() -
разбиения отрезков
-
разбиения отрезков
![]() ,
,
![]() -разбиение
прямоугольника
-разбиение
прямоугольника
![]() ;
под разбиением
;
под разбиением![]() прямоугольника
прямоугольника![]() будем понимать и маленькие прямоугольники
будем понимать и маленькие прямоугольники
![]() .
.
Этих
прямоугольников будет
![]() .
Пусть далее
.
Пусть далее
![]() -
мелкость или диаметр разбиения
-
мелкость или диаметр разбиения
![]() (максимальная диагональ прямоугольников
(максимальная диагональ прямоугольников![]() ),
),
![]() -
разметка разбиения
-
разметка разбиения
![]() ,
,
![]() размеченное
разбиение.
размеченное
разбиение.
В
дальнейшем индексы у прямоугольников
![]() будем опускать, т.е будем писать
будем опускать, т.е будем писать![]() .
.
Определим 3 типа интегральных сумм:
 ,
, 
-
интегральная сумма, отвечающая
размеченному разбиению
![]() ;
;
 -
верхняя сумма Дарбу;
-
верхняя сумма Дарбу; -нижняя
сумма Дарбу.
-нижняя
сумма Дарбу.
Отметим следующие свойства этих сумм
Для любого
 :
: .
.При измельчении разбиения
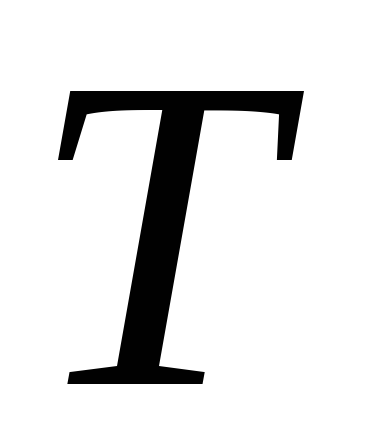 (получается
путем добавления новых точек на
(получается
путем добавления новых точек на или
или )
верхние суммы Дарбу не увеличиваются,
а нижние суммы Дарбу не уменьшаются.
)
верхние суммы Дарбу не увеличиваются,
а нижние суммы Дарбу не уменьшаются.Для любых
 :
: ,
,
Действительно,
если
![]() измельчение как
измельчение как![]() как и
как и![]() то
то![]() .
.
Если
 -
множество всех нижних сумм Дарбу,
-
множество всех нижних сумм Дарбу, -
множество всех верхних сумм Дарбу, то
-
множество всех верхних сумм Дарбу, то и по аксиоме непрерывности существует
и по аксиоме непрерывности существует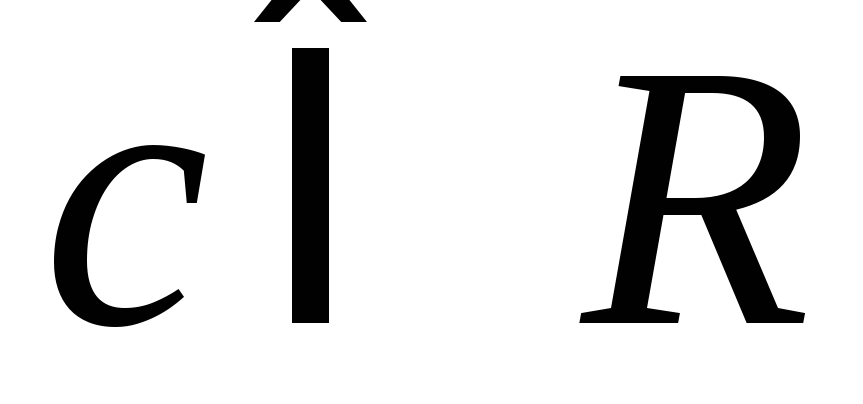 :
: .
.
Определение
1.
![]() -
нижний интеграл Дарбу.
-
нижний интеграл Дарбу.
Определение
2.
![]() -
верхний интеграл Дарбу.
-
верхний интеграл Дарбу.
Для любых
 :
: .
.
Определение 3. Первое определение интеграла Римана.
Будем
говорить, что функция
![]() интегрируема по Риману на прямоугольнике
интегрируема по Риману на прямоугольнике![]() и интеграл равен числу
и интеграл равен числу![]() ,
если существует
,
если существует![]() ,
не зависящий от разметки
,
не зависящий от разметки![]() ,
т.е для любого
,
т.е для любого![]() существует
существует![]() такое, что для любого разбиения
такое, что для любого разбиения![]() и любой разметки
и любой разметки![]() разбиения
разбиения![]() :
:![]() .
.
Будем
писать
![]() .
.
Определение 4. Второе определение интеграла Римана.
Будем
говорить, что функция
![]() интегрируема по Риману на прямоугольнике
интегрируема по Риману на прямоугольнике![]() и интеграл равен числу
и интеграл равен числу![]() ,
если
,
если![]() .
.
