8. Расчет и конструирование элементов сферического покрытия.

   1. Установление габаритных размеров сферического покрытия.

Назначаю стрелку подъема вычисляют радиус сферы купола ( рис. 6 ).Стрелка подъема куполаf :

Радиус сферы:

Центральный угол сферы определяется:

Длина дуги купола в вертикальной плоскости:

Половину длин дуги следует разделить на целое число ярусов щитов покрытия и выделить радиус верхнего центрального кольца. Принимаю длину щита по дуге окружности при этом радиус центрального кольца согласно рис. 6.:

- уплотняют после расчета радиальных ребер. Определяю число щитов в одном ярусе, исходя из ширины щита по опорному кольцу Количество щитов в одном ярусе:

принимаем

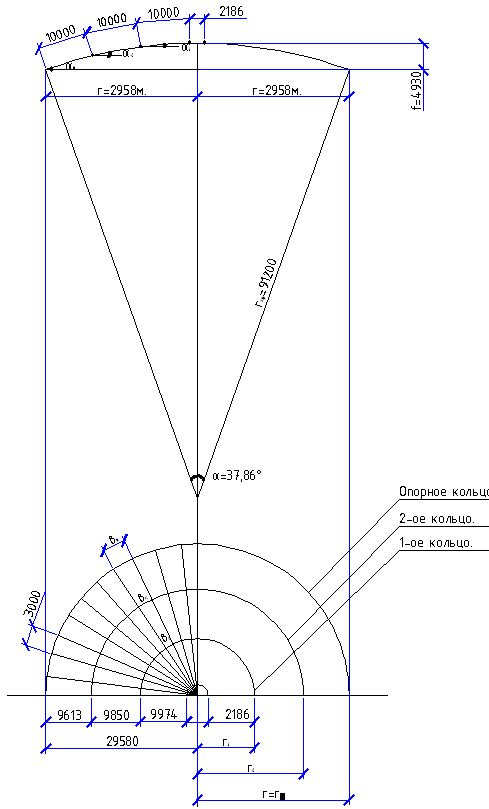
Рис. 6. Схема ребриста – кольцевого купола.

Купол собирается из трех типов трапециевидных щитов, изготовленных на заводе. Расчетными элементами купола являются:

- радиальные ребра;

- промежуточные кольца;

- опорное кольцо;

- настил.

Ширина щитов:

2. Сбор нагрузок на купол.

Нагрузки вертикального направления определяются по формуле:

- направленные вниз;

- направленные вверх;

где - нормативное значение средней составляющей ветровой нагрузке по высоте:

По интрополяции для местности типа В коэффициент, учитывающий изменение ветрового давления по высоте, имеет величину К=0,770.

где- дляIII района; (п. 6)

- знак «-» учтен направлением ветровой нагрузки на покрытие.

Нагрузки горизонтального направления на верхнюю часть резервуара (0,4Н) учитывают:

- нагрузки, вызывающие сжатие опорного кольца купола в виде активного давления ветра и вакуума, определяют по формуле:

где . Коэффициент К находится на высоте

где

- нагрузки, вызывающие растяжение опорного кольца;

ветровой откос и избыточное давление по формуле:

Вертикальная сосредоточенная нагрузка на узел пересечения радиального ребра с кольцом определяется по формуле:

Для 1-го кольца, при

- направленная вверх:

- направленная вниз:

Для 2-го кольца, при

- направленная вниз:

- направленная вверх:

3. Расчет радиального ребра купола.

Наиболее напряженным будет радиальное ребро между опорным и вторым кольцами. Расчетная схема радиального ребра изображена на рисунке 7.

Найдем углы наклона касательной с осью Х в уровнях опорного кольца () и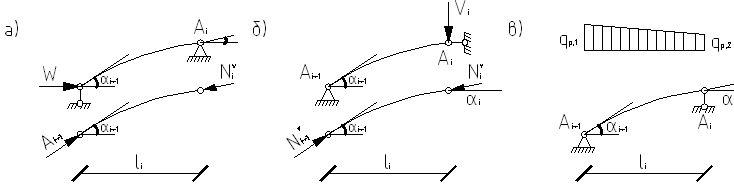2-го кольцапо формуле:

;

Рис. 7. Расчетные схемы радиального ребра купола на нагрузки:

а – горизонтальную; б – вертикальную; в – местную.

; .

.

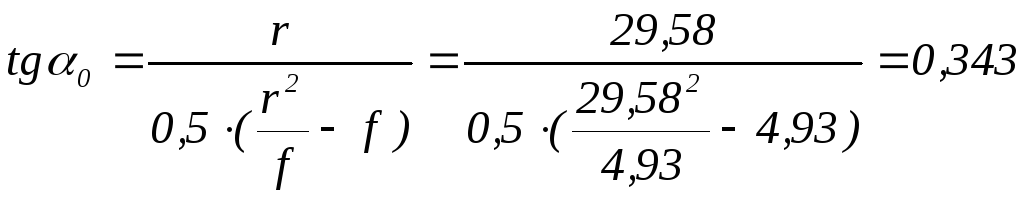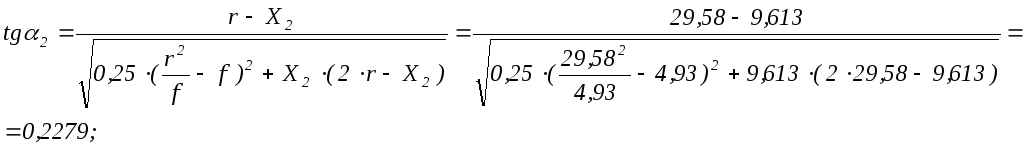
Вычислим в уровне первого кольца при

.

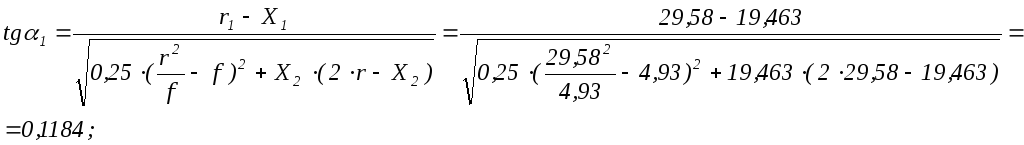
Для опорного радиального ребра средний угол наклона касательных:

;

то же для ребра между вторым и первым кольцами:

.

Определенная вертикальная нагрузка на опорное радиальное ребро находится:

;

.

Продольные сжимающие усилия в опорном ребре:

;

;

, где

.

Суммарное продольное сжимающее усилие в опорном ребре определяется по формуле:

.

Найдем наибольшее значение изгибающего момента в опорном радиальном ребре от распределенной нагрузки (рисунок 8):

Левая опорная реакция:

.

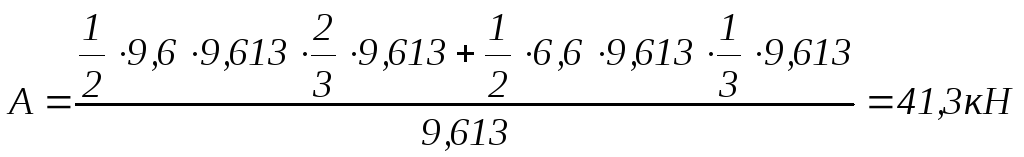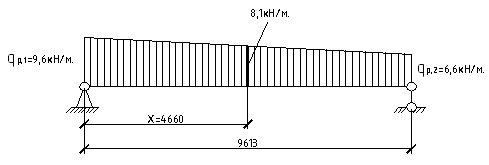
Рис. 8. Схема загружения опорного ребра распределенной нагрузкой.

Найдем положение сечения с наибольшим изгибающим моментом по формуле:

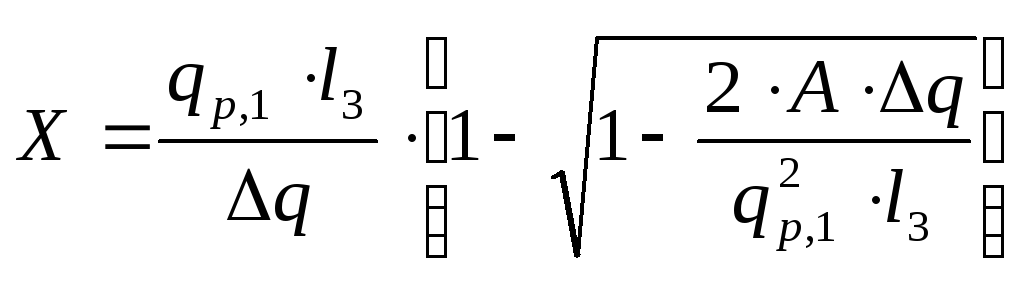
где

.

Максимальное значение изгибающего момента:

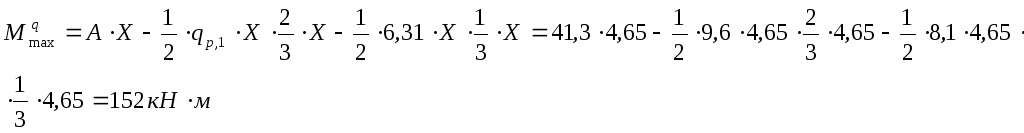
Радиальные ребра конструирую из двух прокатных швеллеров (рисунок 9), из стали марки ВСт3пс6-1 (). Ребро работает на сжатие с изгибом, т.е. на внецентренное сжатие.

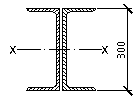
Рис. 9. Сечение радиального ребра. Швеллер № 30.

Считаю, что настил приваривается к радиальным и поперечным ребрам щитов, тем самым обеспечивается устойчивость ребра. Поэтому радиальное ребро буду рассчитывать только на прочность. Задаюсь швеллером №30 () и проверим радиальное ребро на прочность по формуле:;

.

Проверяю принятое сечение радиального ребра на другую комбинацию нагрузок (и), вызывающих растяжение.

Продольные растягивающие усилия в ребре:

;

.

Распределенные нагрузки:

;

.

;

.

Поскольку интенсивность распределенной нагрузки, направленной вверх, меньше интенсивности, направленной вниз, то проверку на прочность ребра по растягивающим усилиям проводить не следует.

Уточню радиус центрального кольца из условия закрепления в нем радиальных ребер щитов из двух швеллеров № 30 (). Учитывая, что ширина двух полок швеллера; толщина промежуточного ребра; зазор 5мм; ширина опирания ребра составит., тогда радиус центрального кольца:.

Длина щита верхнего яруса купола составит:

.

Радиальные ребра радиусов щитов испытывают меньшие нагрузки: и др. Поэтому можно оставить сечение радиальных ребер постоянным из двух швеллеров № 30.