МАТЕМАТИКА ZIP File / Лек бак 2 семестр / Примерыа

5

Примеры нахождения числовых характеристик случайной величины при помощи характеристических функций.

Пример 1. Распределение Пуассона

С учетом того, что для дискретной случайной величины, распределенной по закону Пуассона характеристическая функция имеет вид:

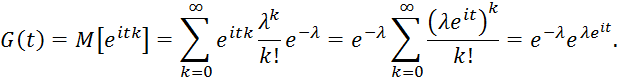
Тогда для математического ожидания получаем:

Для получения дисперсии и других центральных моментов рассмотрим характеристическую функцию центрированной случайной величины:

Представив в виде разложения в ряд получаем

Поскольку моменты случайной величины – это коэффициенты при то имеем: второй центральный момент или дисперсия ;

третий момент ; коэффициент асимметрии .

Пример 2. Нормальное распределение

Рассмотрим нормированную и центрированную случайную величину , функция плотности вероятности имеет вид .

где . С учетом того, что интеграл Пуассона ,

находим .

В результате для переменной получаем:

.

Для центрированной величины :

.

Далее разлагая экспоненту в ряд, получаем

Дисперсия распределения .

Все нечетные моменты .

Распределение полностью симметрично: .

Четвертый момент . Поэтому эксцесс

Пример 3. Пример решения задачи о композиции при помощи характеристической функции

Для показательного закона распределения характеристическая функция имеет вид

Найдем характеристическую функцию суммы каждое слагаемое которой является случайной величиной, распределенной по показательному закону с параметром как произведение характеристических функций:

Тогда числовые характеристики имеют вид:

.

Функцию плотности вероятности можно восстановить через преобразование Фурье:

.

Получили новый закон распределения, который называют законом Эрланга (композиция показательных распределений).

В случае, если не является целым числом, закон называют гамма-распределением, функция плотности вероятности которого имеет вид:

.

.
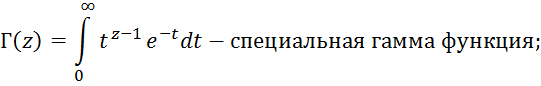