Кратные
интегралы
Лекция 1
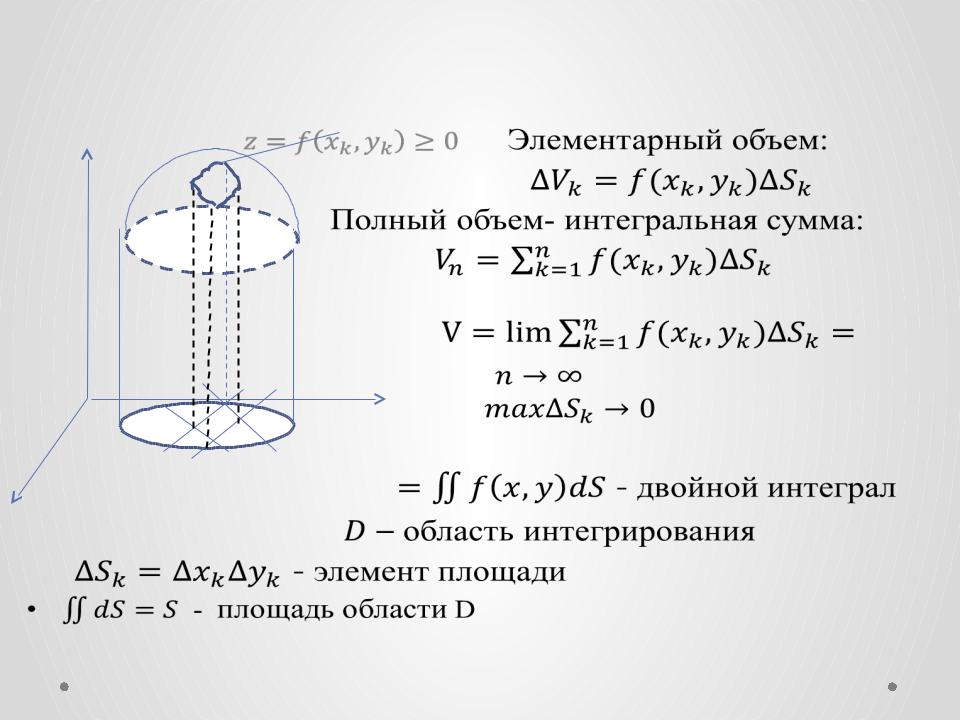
Двойной интеграл. Задача о вычислении объема |
|
• |
Элементарный объем: |
сумма: |
Полный объем- интегральная |
|
|
|
- двойной интеграл |
–область интегрирования
-элемент площади
•- площадь области D
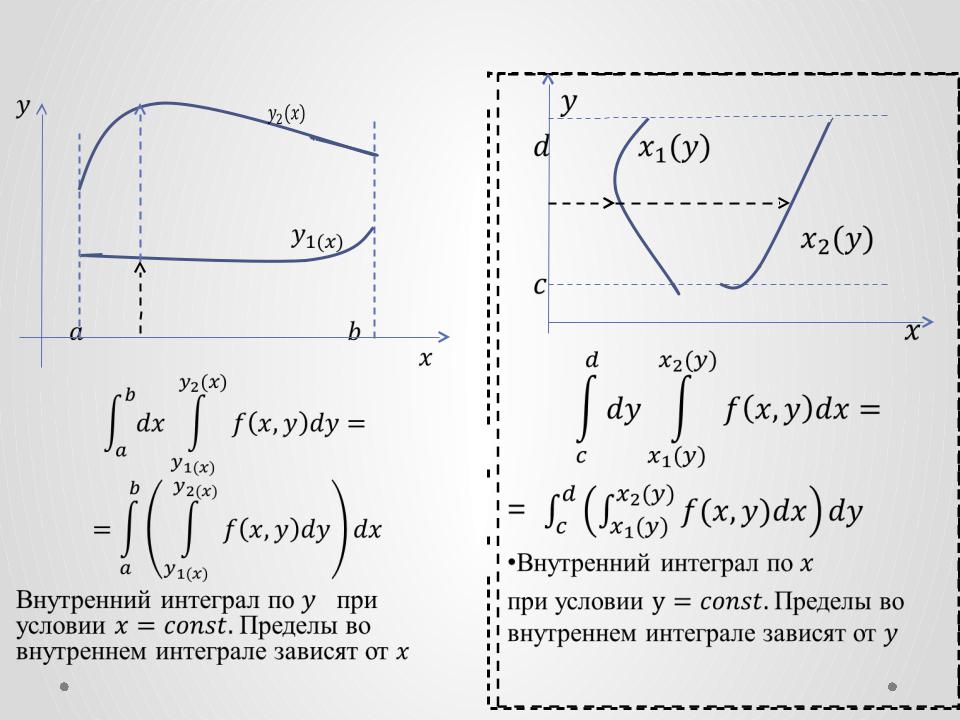
Вычисление двойного интеграла
•
Внутренний интеграл по при условии Пределы во внутреннем интеграле зависят от
•
=
•Внутренний интеграл по
при условии Пределы во внутреннем 
интеграле зависят от
Примеры вычислений двойного интеграла в |
||
декартовых координатах |
|
|
• |
|
|
Пример 1. Вычисляем двойной интеграл по области, заданной |
||
неравенствами |
|
|
y |
= |
|
|
= |
|
Пример 2. Вычислим Внутренний интеграл по |
«неберущийся». Но |
|
интеграл можно вычислить, изменив порядок интегрирования. Область |
||
интегрирования – треугольник: |
|
|
Вычисление двойного интеграла в полярной системе координат
Применяется• в случае, если область интегрирования – круг или его часть: ;
Пример 3. Вычислить Область интегрирования – часть смещенного круга , ограниченная кривыми
=
1 |
Тройной интеграл
Функция• непрерывна в замкнутой ограниченной пространственной области . Тогда тройным интегралом по этой области называют
элемент объема. объем области интегрирования
Вычисление в декартовой системе координат сводится к вычислению однократного интеграла по одной из координат и двойного интеграла по проекции на одну из координатных плоскостей. Пусть область интегрирования ограничена сверху и снизу гладкими поверхностями и однозначно проектируется на плоскость в область
(x , y)
(x,y) Двойной интеграл берется по проекции D 
D
Примеры
Пример• 1. Вычислить по области, ограниченной поверхностью конуса и плоскостями , которая проектируется на плоскость в треугольник:
1 |
1 |
) = = Пример 2. Найти объем тела, ограниченного параболическим цилиндром .
1 |
= |
|
|
|
= |
2 |
|
|
= |
= |
-1 |
1 |
1
Тройной интеграл в цилиндрической системе координат
• z |
Элемент объема |
r |
Пример: Найти объем тела, ограниченного |
параболоидами Параболоиды пересекаются в плоскости по окружности +
Пространственная область проектируется на плоскость в круг +
Записываем уравнения поверхностей в цилиндрической
системе координат :
z
2
2
|
Вычисление тройного интеграла в сферической |
|
|
системе координат |
|
• |
z |
– полярный угол, |
|
r |
азимутальный угол |
|
|
|
|
x |
|
|
|
= |
Пример: найти массу, распределенную по сфере |
||
с плотностью |
|
|
|
= |
|
|
= |
|
|
= |
= |