Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ФИЗИКА3673

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

730.69 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования

šКузбасский государственный технический университетŸ

Кафедра физики

ФИЗИКА

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Комплекс К-402.3. Методические указания по самостоятельной работе для подготовки к выполнению лабораторных работ по разделу физики šМеханические колебания, маятникиŸ

для студентов всех специальностей

Составители: В. В. Дырдин И. С. Елкин

Утверждены на заседании кафедры Протокол № 1 от 28.08.2008 Рекомендованы к печати учебно-методической комиссией специальности 130404 Протокол № 9 от 16.09.2008 Электронная копия находится

в библиотеке главного корпуса ГУ КузГТУ

Кемерово 2008

Содержание

Содержание …………………………………………….…….….….1

Введение……………………………………………………………..2

1. Лабораторная работа № 1 Определение момента инерции физического маятника ………….3

2. Лабораторная работа № 2 Определение момента инерции методом качаний………………...6

3.Лабораторная работа № 3 Определение постоянной кручения нити

баллистическим методом …………………………………...…….11

4.Лабораторная работа № 4

Изучение колебаний физического маятника.……..…….… …….16

5.Лабораторная работа № 5 Изучение механических колебаний

в упруго связанных системах …..……..……………… .………....22

6.Вопросы для самоподготовки………….………..……….…......30

7.Список литературы……………………………………….……..32

ВВЕДЕНИЕ

Комплекс К-402.3 представляет собой необходимый перечень лабораторных работ, предусмотренных образовательным стандартом и рабочей программой по разделу šМеханические колебанияŸ дисциплины šФизикаŸ. Он включает в себя описание лабораторных установок, порядок измерений и алгоритм расчета определенных физических величин.

Лабораторный практикум по физике призван помочь студентам усвоить основные физические явления и законы, ознакомиться с методами физических исследований, приобрести навыки экспериментальных измерений и оценки их результатов, выработать навыки экспериментального решения конкретных задач, умение формулировать постановку задачи, анализировать полученные погрешности измерений и делать вывод о соответствии ожидаемых и полученных результатов.

На самостоятельную работу студента отводится согласно учебному плану около половина учебного времени. Данные методические указания направлены помочь самостоятельно подготовиться и выполнить лабораторную работу. При подготовке к работе студент должен прочитать методические указания к выполнению лабораторной работы, прочитать указанные разделы в учебном пособии или учебнике, составить конспект в соответствие с общепринятыми требованиями. В лаборатории кафедры физики на лабораторной установке студент проводит опыты, результаты которых записываются в таблицы.

После всех расчетов и оформления отчета, студент должен сделать вывод, в котором конкретно указать те физические закономерности, которые были проверены в ходе выполнения работы.

На выполнение каждой из представленных в данном комплексе лабораторных работ отводится два часа аудиторных занятий.

			3
	1. ЛАБОРАТОРНАЯ РАБОТА №1.
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ФИЗИЧЕСКОГО
			МАЯТНИКА
1. Цель работы
Ознакомление с методом экспериментального определения
момента инерции физического маятника.
2. Подготовка к работе
Прочитать в учебниках следующие параграфы: [2] – µµ 16,
140 – 142, [3] – µµ 40, 41. Для выполнения работы необходимо
знать: а) закон динамики вращательного движения твердого тела;
б) основные уравнения кинематики; в) уметь пользоваться изме-
рительными приборами.
3. Выполнение работы
3.1. Описание лабораторной установки
На рис. 1.1 представлена схема используемого в работе фи-
зического маятника. Он состоит из цилиндра массой m1 и радиу-
сом основания R, стержня дли-
ной L и массой m2 и двух грузов
в виде тонких дисков массой m3					m1 О
каждый, которые можно закре-				R
пить на стержне		в нужном по-		R
ложении. Ось колебаний			маят-
ника проходит через точку O.					m2	X C
Грузы m3	располагают на				m3
стержне симметрично на рас-					m3
стояния a от центра масс стерж-					C	a
ня C.				L		a
ня C.
3.2. Методика измерений					m3	a
3.2. Методика измерений
и расчёта
и расчёта		величину m и
Рассчитаем		величину m и
определим	положение		центра
масс маятника:
m m1 m2 2m3 .					X
Для нахождения расстояния				Рис. 1.1. Схема установки
от оси колебаний до центра масс				Рис. 1.1. Схема установки
маятника, проведем ось OX с на-

чалом в оси колебаний (в точке O). Координата центра масс механической системы находится по формуле

X C

mi xi

(1.1)

где xi – координата центра масс i-го тела. В нашем случае

X1 0 ,

X 2

R ,

R a ,

X 4

R a .

Подставляя в (1.1), получаем

2m )(

X С

(1.2)

Отсюда видно, что положение центра масс маятника не за-

висит от положения грузов m3(a)

при их симметричном распо-

ложении относительно середины стержня.

Подставляя в формулу T 2π

, получаем рабочую

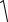mgXC

формулу для экспериментального определения момента инерции физического маятника:

I э	gT 2	(m	2m )(	L	R).	(1.3)

	4 2	2	3	2

Для удобства расчетов обозначим через K следующее выражение:

	g(m 2m )(		L	R)

2		3	2
K					,	(1.4)
		4π2

где K – постоянная для данного физического маятника величина.
Тогда
	I э KT 2 .					(1.5)
Период колебаний физического маятника, а значит и его
момент инерции зависят от положения грузов m3						на стержне,

т. е. от значения величины a . Найдем эту зависимость. Для этого рассчитаем момент инерции физического маятника теоретически. Так как момент инерции механической системы – величина аддитивная, то момент инерции маятника равен сумме моментов инерции всех составляющих его тел:

																			I т I	I	2	I		3	I		4	.
				1 m R 2															1		2			3			4
I				1 m R 2															– момент инерции цилиндра;
	1			2	1								L
				2
I2				1	2													2	– момент инерции стержня,
I2			12 m2L m2									(	2		R)				определенный по теореме Штейнера;
I		m ( L R a)2																	– моменты инерции тонких дисков m3 ,
	3		3				2												которые можно принять за материаль-
						L							2						ные точки.
I4 m3(								R a)					2						ные точки.
I4 m3(						2		R a)
Тогда										1							1									L
							I т			1	m1R2						1		m2 L2 (m2			2m3 )(				L		R)2 2m3a2	(1.6)
							I т				m1R2								m2 L2 (m2			2m3 )(						R)2 2m3a2	(1.6)
					2										12										2
или																			I т I 0 2m a2
																			I т I 0 2m a2						,				(1.7)
																			1			3
где				I10	1				m1R2				1			m2L2 (m2				2m3 )(			L		R)2 – момент инерции

								2						12									2

маятника при a 0 , т. е. при расположении грузов m3 в точке C. Из формулы (1.7) видно, что момент инерции физического

маятника линейно зависит от a 2 . Эта зависимость проверяется в работе экспериментально.

3.3. Измерение момента инерции маятника

3.3.1.Заполните табл. 1.1 и рассчитайте по формуле (1.4) постоянную физического маятника K.

3.3.2.Поместите оба груза m3 в середине стержня ( a 0 ).

Отклоните маятник на угол 5–6¹ и определите время t десяти полных колебаний маятника. Повторите опыт 5 раз, рассчитайте

t и период колебаний T t 10 . По формуле (1.5) рассчитайте момент инерции маятника. Данные занести в табл. 1.2.

	Характеристики установки			Таблица 1.1
	Характеристики установки

m2	m3	L	R	K
кг	кг	м	м	кг∙м2 с–2

3.3.3. Измените положение грузов m3 на стержне и для четырех, указанных в таблице значений a, повторите измерения и расчеты, описанные в 3.3.2.

Оцените погрешность измерений.

3.3.4. Постройте график зависимости I f (a2 ).

3.4. Сделайте вывод о соответствии полученного графика формуле (1.7).

Таблица 1.2

Определение момента инерции маятника

а	a2	t	t	T	I э	I т
м	м2	с	с	c	кг»м2	кг»м2
0
0,10
0,15
0,20
0,25

2. ЛАБОРАТОРНАЯ РАБОТА №2.

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МЕТОДОМ КАЧАНИЙ

1. Цель работы

1.1.Освоить метод экспериментального определения момента инерции диска с вырезом.

1.2.Теоретически рассчитать момент инерции диска с вырезом и сравнить его с экспериментальным.

2. Подготовка к работе

Прочитать в учебниках следующие параграфы: [2] – µµ 16, 140 – 142, [3] – µµ 40, 41. Для выполнения работы необходимо знать: а) закон динамики вращательного движения твердого тела; б) уметь пользоваться измерительными приборами.

3. Выполнение работы 3.1. Описание лабораторной установки

Установка для определения момента инерции твердого тела

методом качаний (рис. 2.1) состоит из призмы		1, прикрепленной
с помощью штифта к вертикальной	стойке 2. Стойка установле-
на в литой чугунной треноге 3,
две ножки которой снабжены	1
винтами 4. Это позволяет регу-	1
винтами 4. Это позволяет регу-
лировать установку по уровню 5
так, чтобы опорное ребро приз-
мы приняло горизонтальное по-
ложение. Грань призмы является		6
осью качаний тела, имеющего		6
отверстие. К стойке прикреплена	2
планка 6 клиновидной формы с	2
углом при вершине 4О, которая	5	3
является визиром, позволяющим		4
следить за тем, чтобы размах ко-
лебаний не превышал 7О.
На призму 1 устанавлива-	Рис. 2.1. Схема установки
ется диск с вырезом, колебания	Рис. 2.1. Схема установки
ется диск с вырезом, колебания
которого исследуются в данной
работе.
3.2. Методика измерений и расчёта

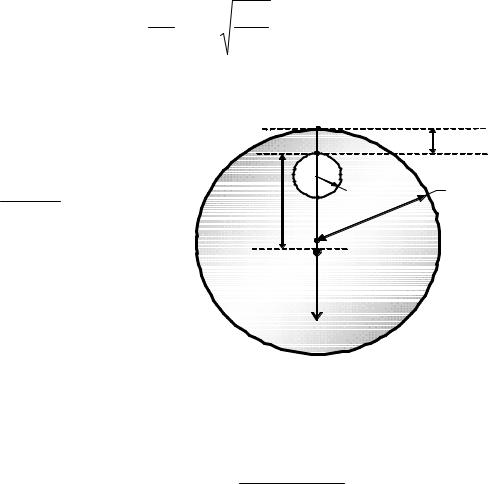
Момент инерции тела может быть определен экспериментально по методу качаний. В данной работе тело представляет собой однородный диск радиусом R , в котором вырезано отверстие радиусом R0 (рис. 2.2) Диск с вырезом может совершать колебания под действием силы тяжести относительно оси (опора D ), не проходящей через центр масс (точка C ). Такое тело называется физическим маятником. Период колебаний T физического маятника:

T 2π 2π

J .

(2.1)

ω0

mgl

Из формулы (2.1) выра-

зим момент инерции диска J

относительно оси колебаний:

mglT

(2.2)

4 2

где

–

период

колебаний;

l – расстояние

от

оси коле-

баний до центра масс маят-

ника.

Если начало отсчета по

оси

взять

точке

Рис. 2.2. Диск с вырезом

(рис. 2.2),

тогда

координата

центра инерции yc l

mi yi

или y

m1y1 m2 y2 ,

где m1 (m m0 ) масса сплошного диска; y1 (R l0 ) координата центра сплошного диска; m2 m0 – масса вынутой части диска; y2 R0 – координата центра вынутой части диска.

Подставляя значения масс и координат в формулу для yc ,

получим:
yc l	(m m0 )(R l0 ) m0 R0	.	(2.3)

	m

Массу вырезанной части можно определить косвенно:

mm0 ρν ρπ R 2 h,

m0 ρv0 ρπ R02 h.

Выражая из нижнего соотношения h и подставляя в верхние, получим, что

			mR2
	m0		0	.				(2.4)
	m0		R2 R2	.				(2.4)
			0
Подставляя	(2.4) в (2.3),		получим
		[R2 (R l ) R3				]
	l		0		0		.	(2.5)
	l		R2 R2				.	(2.5)
			R2 R2
			0
Рассчитав l	и экспериментально определив период колеба-

ний Т вычисляют момент инерции диска с вырезом. Момент инерции диска с вырезом можно рассчитать и теоретически по формуле (2.1), используя свойство аддитивности момента инерции:

J т J1 J 2 ,

(2.6)

где J1 момент инерции сплошного диска (без выреза) относительно оси; J2 момент инерции вырезанной части относительно той же оси.

Моменты инерции J1 и J2 рассчитывают по теореме Штей-

нера:
		(m m )R2								)2
J	1			0			(m m )(R l				,	(2.7)
J							(m m )(R l				,	(2.7)
				2				0	0
				2
		J	2		m0R02	m R2.						(2.8)
		J				m R2.						(2.8)
				2		0		0
				2

Подставляя (2.7) и (2.8) в (2.6) и учитывая (2.4), получают теоретическое значение момента инерции диска с вырезом отно-

сительно оси вращения:
		m[R4	2R	2 (R l	0	)2	3R4	]
J	т				0		0		.	(2.9)
J			2(R2 R2 )						.	(2.9)
			2(R2 R2 )
				0

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.05.2015368.1 Кб45Физика лаб 1,2.pdf
#
10.05.20151.52 Mб69физика,Лабораторные.doc
#
10.05.2015461.99 Кб236Физика. К-310.2.pdf
#
10.05.2015386.31 Кб308Физика. К-315.1.pdf
#
10.05.2015902.14 Кб58Физика. лаб 3.doc
#
10.05.2015730.69 Кб25ФИЗИКА3673.pdf
#
10.05.2015735.65 Кб97Физическая химия в 2 кн. Ч. 2..pdf
#
10.05.2015552.23 Кб64Физическая химия Обучающая программа.pdf
#
10.05.20151.03 Mб188Физическая химия Часть 1 учебное пособие.pdf
#
20.04.2019111.64 Кб7философия попытка № 2.docx
#
10.12.2018591.36 Кб11ФИЛОСОФИЯ РЕПЕТИЦИОННОЕ.doc