Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Линейная алгебра (2 к р)

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

261.16 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

€К у з б а с с к и й г о с у д а р с т в е н н ы й т е х н и ч е с к и й

ун и в е р с и т е т и м е н и Т . Ф . Г о р б а ч е в а €

Кафедра математики

ЛИНЕЙНАЯ АЛГЕБРА

Контрольная работа № 2 и методические указания для студентов 2 курса (4 семестр)

направления 080100.62 ©Экономика« заочной формы обучения

Составители В. М. Волков Е. А. Волкова А. И. Бабин

Утверждены на заседании

кафедры

Протокол № 7 от 16.05.2013 Рекомендованы к печати учебно-методической комиссией

направления 080100.62 Протокол № 28 от 22.05.2013

Электронная копия находится в библиотеке КузГТУ

Кемерово 2013

Контрольная работа № 2 составлена в соответствии с программой курса алгебра для студентов-заочников. В составлении работ и методических указаний к ним принимали участие преподаватели: В. М. Волков.

Номера задач контрольных работ студент должен выбрать по таблице ©Выбор номеров контрольных задач« следующим образом:

найти строку, соответствующую первой букве фамилии;

найти столбец, соответствующий последней цифре шифра;

на пересечении найденных строки и столбца взять номера

задач контрольной работы № 2.

Контрольные работы, выполненные не по своему варианту, возвращаются непроверенными.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ

Контрольная работа №2 При решении задач № 1-30 следует проработать тему ©Пре-

образование координат при переходе к новому базису« [1, 2].

Пример. Найти координаты вектора x 6, 1,3 в базисеe1 ,e2 ,e3 , если он задан в базисе e1 ,e2 ,e3 , где

e1 e1 e2 2e3 ,

e2 2e1 e2 ,

e3 e1 e2 e3 .

Решение. Строки матрицы перехода от старого базиса к новому являются коэффициентами в формулах преобразования координат. Подставим в систему e1 6,e2 1,e3 3 , получим систему:

e1 e2 2e3 6,2e1 e2 1,

e1 e2 e3 3.

Решив данную систему методом Гаусса или методом Крамера, получим e1 1,e2 3,e3 1.

					Выбор номеров задач контрольных работ

№		0		1	2			3		4		5		6		7		8		9
А,В,Д	1 31 80		2 32 79		3 33 78		4 34 77		5 35 76		6 36 75		7 37 74		8 38 73		9 39 72		10	40
	110		100		101		120		91		110		111		100		101		71	120
Ё,Е,З	11	41	12	42	13	43	14	44	15	45	16	46	17	47	18	48	19	49	20	50
	70	109	69	99	68	102	67		66	92	65	109	64	112	63	99	62 102		61 119
							119
Г,Ж,И,	21	51	22	52	23	53	24	54	25	55	26	56	27	57	28	58	29	59	30	60
Л	80	108	79	98	78	103	77		76	93	75	108	74	113	73	98	72		71
							118										103		118
К	1 60 90		2 59 69		3 58 88		4 57 87		5 56 86		6 55 85		7 54 84		8 53 83		9 52 82		10	51
	107		97		104		117		94		107		114		97		104		81	117
М,Н,О	11	49	12	48	13	47	14	46	15	45	16	44	17	43	18	50	19	42	20	41
	70	106	61	96	62	105	63	116	64	95	65	106	66	115	67	96	68		69	116	2
																	105
П,Ы	21	31	22	32	23	33	24	34	25	35	26	36	27	37	28	38	29	39	30	40
	80	105	71	95	72		73	115	74	96	75	105	76	116	77	95	78	106	79	115
					106
С,У,Б	1 60 90		2 59 81		3 58 82		4 57 83		5 56 84		6 55 85		7 54 86		8 53 87		9 52 88		10	51
	104		94		107		114		97		104		117		94		107		89	114
Р,Т,Ф	11	50	12	49	13	48	14	47	15	46	16	45	17	44	18	43	19	42	20	43
	70	104	61	96	62		63		64	98	65		66	118	67	93	68	108	69	113

					108		113				103
Х,Ц,Ш	21	40	22	39	23	38	24	37	25	36	26	35	27	34	28	33	29	32	30	31
	80 112		71	92	72	109	73	112	74	99	75	102	76	119	77	92	78	108	79
																			112
Ч,Щ,Э	1 51 90		2 52 82		3 53 81		4 54 83		5 55 65		6 55 84		7 57 86		8 58 87		9 59 88		10	60
Ю,Я	101		91		110		111		100		101		120		91		110		89	111

Следовательно, вектор x в новом базисе имеет вид

x 1,3,1 .

Для решения задач 31-60 необходимо разобрать тему ©Линейные преобразования и матрицы« [1, 2].

Пример. Найти характеристические числа и собственные векторы матрицы:

	3	1	1
		5	1
1				.
	1	1	3

Решение. Составляем характеристическое уравнение:

3	1	1
1	5	1	0 ,
1	1	3

или 3 5 3 3 1 1 5 0 . После

преобразований уравнение приводится к виду

3 2 8 12 0 , откуда 1 2, 1 3, 1 6 .

Находим собственный вектор, соответствующий характеристическому числу 1 2 . Из системы уравнений

e1 e2 e3 0,e1 3e2 e3 0,

e1 e2 e3 0

полагая, например, e2 0 найдём e3 e1 . Пусть e1				. Тогда
			.
собственный вектор r1 i k			.
Находим собственный вектор, соответствующий
характеристическому числу 2			3 . Из системы уравнений
		e 2 e 3 0,

		e1 2e2 e 3 0,

		e1 e2 0			i j k .
найдём e	e
найдём e	e	e . Тогда собственный вектор r
1	2	3	2

Находим собственный вектор, соответствующий характеристическому числу 3 6 . Из системы уравнений

		4
		3e1 e2 e3 0,

		e1 e2 e3 0,

		e1 e2 3e3 0
найдём e1 ,e2 2 ,e3 . Тогда собственный вектор

r3	i 2 j k .		i k ,

	Итак, собственные векторы матрицы имеют вид r1
		i 2 j k , где , , - произвольные отличные
r2	i j k , r3	i 2 j k , где , , - произвольные отличные

от нуля числа.

Более подробный теоретический материал и практические рекомендации по данной теме (№ 61-90) можно найти, например, в следующих учебниках: [3, 4].

Комплексными числами называются числа вида

z x i y , где

i2 1,

x, y – действительные

числа, x Re z – действительная

часть,

y Im z – мнимая часть комплексного числа.

По

определению,

два

комплексных

числа:

z1 x1 i y1

i y2 – равны

тогда и

только тогда, когда x1 x 2

y2 .

Комплексное число

называется

сопряженным

комплексному числу

z , если

Re z,

Im z . Другими

словами, если	z x i y , то			z	x i y .
Всякому комплексному				числу		x i y	можно поставить в
соответствие единственную точку плоскости M(x, y)									и обратно,
всякую точку	M(x, y) плоскости					XOY	можно рассматривать
как геометрический		образ		единственного			комплексного			числа
x i y .
y			Множество всех					действительных
			чисел изображается					точками		оси
	М		абсцисс, которая поэтому называется
			действительной				осью,		множество
			чисто мнимых чисел i y						точками
0		х	оси ординат,

Рис. 1

называемой мнимой осью. Заметим, что одна точка мнимой оси, а именно начало координат, изображает действительное число нуль. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.

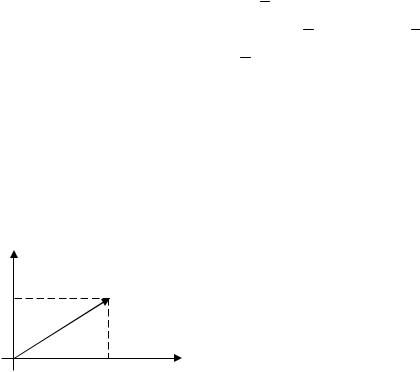
Внекоторых случаях удобно считать геометрическим

изображением числа			x i y радиус-вектор точки				M(x, y)	–
O M x, y .
y			Пример. Построить точки
			z1 5 5i ,	z2 2i ,		z3 5.
0	z3
			В дальнейшем,			наряду		с
	5	x
-2 z2			представлением комплексных

			чисел	в		декартовых

-5	z1		координатах, полезно иметь их
			представление		в обобщенных

Рис. 2			полярных координатах.
			Рассмотрим		число		x i y ,
			которому		на	плоскости
			соответствует		точка		M(x, y) .

M(x; y)

Рис. 3

Ее координаты		в	полярной
системе координат			, .
Тогда x cos ,
y sin .
z x i y cos i sin
cos i sin .
Полярный радиус				OM
Полярный радиус				OM
называется			модулем
комплексного		числа			и
обозначается	z	.

, .

Полярный угол называется аргументом комплексного числа и обозначается Arg z . Тогда

z cos i sin z cos Arg z i sin Arg z .

Эта форма называется тригонометрической формой комплексного числа.

Модуль комплексного числа определяется однозначно:

z x2 y2 .

Аргумент комплексного числа определяется с точностью до слагаемого, кратного 2 . Главным значением аргумента называется значение, заключенное в интервале Обозначается оно arg z . Таким образом, arg z .

Очевидно, Arg z arg z 2k .

Главное значение аргумента определяется однозначно.

Так как tg arg z y ,

	x
	y			x, y I, IV четвертям,
arctg		,	если
	x
				x, y II четверти,
	y

arg z arctg		,	если
	x
				x, y III четверти.
	y
arctg		,	если
	x

Тригонометрическая форма комплексного числа будет иметь

вид z z cos arg z 2k i sin arg z 2k .

Пример. Написать в тригонометрической форме комплексное

	y		число		z 1 i .
			Решение.				z					tg 1,
			Решение.				z		1 1		2,	tg 1,
z	1			arg z arctg 1											3	.
z	1			arg z arctg 1												.
										4				4
-1	0	x				3							3
-1	0	x				3							3
	Рис. 4		z 2		cos			2k		i sin				2k			.
			z 2		cos			2k		i sin			4	2k			.
						4							4

					7
Пусть	z x i y	z	cos Arg z i sin Arg z . Используя формулу
Пусть	z x i y	z	cos Arg z i sin Arg z . Используя формулу
Эйлера	cos i sin ei ,					получаем так называемую
показательную форму записи комплексного числа:
			z	z		ei Arg z .
			z	z		ei Arg z .

Пример. Представить в показательной форме комплексное

число z 1 i .		Решение.
	y	Решение.
-1	0		z		1 1	2,		tg 1,
			z		1 1	2,		tg 1,
									3
	x			arg z					3	,
	x			arg z						,
		4						4
							3	i 2k i
							3	i 2k i
			1 i 2 e				4	.

z-1

Рис. 5

Пример. Вычислить e i .

Решение. По формуле Эйлера e i cos i sin 1.

Для выполнения алгебраических действий над комплексными числами (№ 91-120) необходимо проработать литературу: [3, 4], где содержатся теоретический материал и практические рекомендации по данной теме.

Сложение и умножение комплексных чисел производится по правилам сложения и умножения алгебраических многочленов с учетом i i 1. При записи результата следует отделить действительную часть от мнимой, т. е. собрать отдельно члены,

содержащие множитель			i ,	и члены, не содержащие множитель
i : x1 i y1 x2 i y2 x1 x2 i y1 y2 ,
x1 i y1 x2 i y2 x1 x2 y1 y2 i x1 y2 y1 x2 ,
x1 i y1 x2 i y2 x1 x2 i y1 y2 .
В частности, z	z	z	2 .	Операции сложения и вычитания

сводятся к сложению и вычитанию векторов, изображающих эти числа. Отсюда расстояние между точками z1, z2 z1 z2 .

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.07.2025207.65 Кб0лекция ЭС металл5-6 + вопросы.docx
#
16.12.201899.84 Кб3Лекция. Риск..doc
#
10.05.20154.78 Mб61Лекцияри нов.doc
#
03.08.201971.68 Кб3Лекция№7_1.doc
#
10.05.2015879.64 Кб64Лемескина Т.В. Ценообразование.pdf
#
10.05.2015261.16 Кб8Линейная алгебра (2 к р).pdf
#
09.11.20191.16 Mб9Линейные цепи синусоидального тока.doc
#
10.05.2015712.7 Кб34Лицензирование и сертефикация.pdf
#
01.05.202560.83 Кб0Лицензирование моя.docx
#
01.05.20251.05 Mб0лицензирование.doc
#
10.05.2015223.91 Кб121Логика.docx