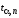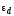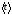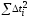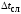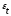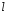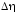Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

Учреждение высшего профессионального образования

«Кузбасский государственный технический университет

имени Т.Ф. Горбачева»

Кафедра физики

Отчет

по лабораторной работе № (К 304.1) 2

«Определение коэффициента внутреннего трения

жидкости методом Стокса»

Выполнил ст. группы МРб-121

Романов И. А.

(Ф.И.О.)

Преподаватель

Фофанов А. А.

(Ф.И.О.)

Цель работы: 

1) изучить особенности движения тела в вязкой среде;

2) познакомиться с методами определения коэффициента внутреннего трения;

3) определить коэффициент внутреннего трения жидкости методом Стокса.

Приборы и принадлежности: цилиндр с жидкостью (маслом), железный шарик, секундомер, магнит, линейка, штангенциркуль, воронка.

Схема экспериментальной установки

Где:

m - сила тяжести

– сила сопротивления среды

– сила Архимеда

-ускорение

Основные расчетные формулы:

среднее арифметическое значение результатов измерений

где – результат i-го измерения, – число измерений

абсолютные погрешности отдельных измерений₁

;;. . .;.

среднее квадратичное отклонение от среднего арифметического из 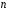измерений

.

истинное значение 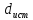измеряемой величины _d окажется в интервале

,

который называют доверительным интервалом.

случайная погрешность

.

где:

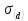- средняя квадратичная погрешность

t_α,n – коэффициент Стьюдента.

абсолютная погрешность

.

где:

_пр– практическая погрешность

_сл – случайная погрешность

результаты прямых измерений записываются в виде

.

коэффициент внутреннего трения η

где – расстояние между метками на измерительном цилиндре с маслом; – время равномерного движения шарика.

относительная погрешность измерений диаметра_d

%.

относительная и абсолютная погрешность результата косвенных измерений коэффициента внутреннего трения:

,

где ; – абсолютная погрешность, которая равна цене деления шкалы линейки, с помощью которой измеряется расстояние, пройденное шариком при установившемся движении,

.

Результат вычислений записать в виде:

.

Таблица 1

Результаты измерения диаметра шарика и расчета

погрешностей

№
	мм	мм	мм	мм2	мм2	мм	a= 0,95	мм	мм	мм	%	мм
1	1,74	1,748	0.008	0.000064	0.00048	0.0048	2.78	0.013	0.01	0.016	0.91	1.748±0.013
2	1,74		0.008	0.000064
3	1,76		0.012	0.000144
4	1,76		0.012	0.000144
5	1,74		0.008	0.000064

Таблица 2

Результаты измерения времени падения шарика и расчета погрешностей

№ п/п
	с	с	с	с2	с2	с	a= 0,95	с	с	с	%	с
1	19,3	18.5	0.8	0.64	0.94	0.216	2.78	0.6	0.1	0.6	3.2	18.5±0.6
2	18,0		0.5	0.25
3	18,4		0.1	0.01
4	18,3		0.2	0.04
5	18,5		0.0	0.0

Таблица 3

Результаты измерения коэффициента внутреннего трения

м	м	с	кг/м3	кг/м3	Па · с	%	Па · с
0.001748	0.178	18.5	7900	960	1.19	3.7	0.044

Примеры расчетов:

; ; . . .;

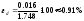
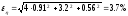
Вывод: Полученное значение коэффициента внутреннего трения жидкости методом Стокса составило (1.27±0.046) .

Сначала движение шарика было ускоренным, т.к. вязкость воздуха мала, после попадания в жидкость шарик начал двигаться равнозамедленно и на него действовали силы:,

После уравновешивания всех сил шарик начал двигаться равномерно. Формула вязкости жидкости была получена из второго закона Ньютона для n-ого движения шарика.

Романов И.А.