15

Индивидуальные задания

«Технология транспортных процессов» бакалавры

5. Электростатика и электромагнетизм Характеристики электростатического и магнитного полей

- напряженность и потенциал электростатического поля;

- принцип суперпозиции электростатических полей;

- связь напряженности и потенциала;

- напряженность и потенциал поля точечного заряда;

- теорема Гаусса для поля в вакууме;

- напряженность поля плоскости;

- напряженность поля конденсатора;

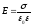- напряженность поля нити;

- энергия и объемная плотность энергии электростатического поля;

- индукция магнитного поля;

– закон Био-Савара-Лапласа;

– закон полного тока для стационарных полей в вакууме;

– принцип суперпозиции магнитных полей;

– индукция магнитного поля длинного прямого тока;

– индукция магнитного поля прямого отрезка проводника;

– индукция магнитного поля в центре кругового тока;

– индукция магнитного поля длинного соленоида;

– энергия и объемная плотность энергии магнитного поля.

Проводники в электрическом поле

, - электроемкость проводника, конденсатора;

- электроемкость шара;

- емкость плоского конденсатора;

- общая емкость при параллельном соединении конденсаторов;

- общая емкость при последовательном соединении конденсаторов;

- энергия заряженного проводника;

- энергия заряженного конденсатора.

Электрический ток. Законы Ома и Джоуля-Ленца

- сила и плотность тока;

- закон Ома и Джоуля-Ленца в локальной форме;

- сопротивление проводника;

- общее сопротивление при последовательном соединении;

- общее сопротивление при параллельном соединении;

- закон Ома для однородного участка цепи;

- закон Ома для замкнутой цепи;

- полезная мощность тока.

Магнитный поток. Явление электромагнитной индукции

; – определение магнитного потока;

– работа поля по перемещению контура с током в магнитном поле;

– индуктивность соленоида;

ε_i – закон Фарадея для электромагнитной индукции;

– разность потенциалов на концах движущегося проводника.

Примеры решения задач

Задача 1

Два одинаковых положительных заряда 10^-7 Кл находятся в воздухе на расстоянии 8 см друг от друга. Определить напряженность в точке О, находящейся на середине отрезка, соединяющего заряды, и в точке А, расположенной на расстоянии 5 см от зарядов.

Дано:

2r= 8 см = 0,08 м

r₁ = 0,05 м

Найти

Е₀ и Е.

Решение: Напряженность поля, создаваемого зарядами, находится по принципу суперпозиции. Результирующая напряженность определяется векторной суммой напряженностей, создаваемых каждым зарядом в данной точке поля:

, (1)

где и - величины напряженностей полей, определяемых по формуле

(2)

Чтобы найти числовые значения напряженности в точке О, надо сначала построить векторы напряженностей и . Кроме того, заряды равны и расположены на равном расстоянии от точки О. С учетом направления векторов из формул (1) и (2) следует:

.

В точке А результирующий вектор напряженности является диагональю параллелограмма (см. рис.), следовательно, или , т.к. . Численное значение напряженности поля в точке А

Задача 2

Два одинаковых плоских воздушных конденсатора ёмкостью по 100 пФ каждый соединены в батарею последовательно. На сколько изменится ёмкость батареи, если пространство между пластинами одного из конденсаторов заполнить парафином с диэлектрической проницаемостью 2.

Решение

Общую ёмкость при последовательном соединении конденсаторов С₁ и С₂ можно: найти из формулы: . Поэтому общая ёмкость батареи, состоящей из двух одинаковых конденсаторов ёмкостью С₀ (до заполнения одного из конденсаторов парафином) равна: . После заполнения парафином одного из конденсаторов его ёмкость , а до заполнения была равна , то есть ёмкость возросла в ε раз: . Найдём новую общую ёмкость батареи: . Таким образом, изменение ёмкости батареи равно: . Подставим численные значения: .

Ответ: .

Задача 3.

Электрическое поле создано в вакууме заряженной (Q=0.2 мкКл) металлической сферой радиусом 5 см. Какова энергия поля, заключенного в сферическом слое, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в 3 раза больше радиуса сферы?

Решение:

Энергию поля, заключенную в сферическом слое, найдем через объемную плотность энергии

, (1)

а энергия электростатического поля

. (2)

Напряженность электростатического поля, созданного уединенной металлической заряженной сферой, вне этой сферы (при r>R₀):

, (3)

где ε=1.

Из (1) – (3) следует, что энергия, заключенная в любом малом объеме dV, равна:

. (4)

Для сферически симметричного поля в качестве dV следует брать тонкий шаровой слой, концентрический данной сфере, с внутренним радиусом r, внешним радиусом (r+dr), тогда в пределах этого слоя значение напряженности можно считать одинаковым и равным (3). Объем слоя:

. (5)

Энергию находим, проинтегрировав (4) по объему, то есть в пределах R₀<r<R:

,

.

Ответ: W=2.4 мДж.

Задача 4.

Сила тока в проводнике сопротивлением 12 Ом равномерно убывает от максимального значения до нуля за 10 с. Определить количество теплоты, выделившееся в этом проводнике за указанный промежуток времени, если по проводнику прошел заряд 50 Кл?

Решение:

Закон изменения со временем силы тока в проводнике:

I=I₀–kt, (1)

где – быстрота убывания тока:

(2)

Заряд, прошедший через сечение, можно рассчитать, интегрируя силу тока по времени в рассматриваемом промежутке: так как , то

,

с учетом (2):

. (3)

Количество выделившейся теплоты находим по закону Джоуля-Ленца, подставив (1):

. (4)

Здесь учтено, что из (2) I₀=kt₀.

Из (3) , тогда .

Вычисляем: .

Ответ: Q=4000 Дж

Задача 5.

Два параллельных бесконечно длинных провода D и C, по которым текут в одном направлении токи силой I = 60 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию поля, создаваемого проводниками с токами в точке A (см. рис.), отстоящей от оси одного проводника на расстояние r₁ = 5 см, от другого r₂ = 12 см.

Рис. 3.

Решение: Для нахождения магнитной индукции в точке A воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитной индукции и полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:

.

Величина магнитной индукции может быть найдена по теореме косинусов:

. (1)

где  – угол между векторами и . Значения магнитной индукции и выражаются соответственно через силу тока I и расстояние и от проводников до точки A:

.

Подставляя выражения и в формулу (2), получим:

. (2)

Для вычисления , учтем, что (как углы с соответственно перпендикулярными сторонами), и по теореме косинусов запишем:

,

где d – расстояние между проводами. Отсюда:

.

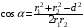После подстановки числовых значений получим:

Подставляя в формулу (2) значения входящих величин, определяем индукцию магнитного поля:

Задача 6.

Электрон, пройдя ускоряющую разность потенциалов равную 400 В, попал в однородное магнитное поле напряжённостью . Определить радиус R кривизны траектории и частоту n обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля.

Решение. На движущийся в магнитном поле электрон действует сила Лоренца (действием силы тяжести можно пренебречь). Сила перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение. По второму закону Ньютона можно записать

,

где - нормальное ускорение или

(1)

где - заряд и скорость электрона; R – радиус кривизны траектории;  – угол между направлением вектора скорости и вектором (в данном случае и  = 90, ).

Из формулы (1) найдём

(2)

Входящий в равенство (2) импульс может быть выражен через кинетическую энергию W_K электрона:

(3)

Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством:

Подставив это выражение W_K в формулу (3), получим

Магнитная индукция B связана с напряжённостью H магнитного поля в вакууме:

,

где - магнитная постоянная.

Выражения B и подставим в формулу (2)

. (4)

Значения констант, входящих в формулу (4):

, , .

Произведём вычисления радиуса кривизны траектории электрона:

.

Для определения частоты обращения n воспользуемся формулой, связывающей частоту обращения со скоростью и радиусом:

(5)

Подставив в формулу (5) выражение (2) для радиуса кривизны, получим:

.

Проведём вычисления:

.

Задача 7.

Соленоид с сердечником из магнитного материала содержит N = 1200 витков провода, прилегающих друг к другу. При силе тока I = 4 А магнитный поток Ф = 6 мкВб. Определить индуктивность L соленоида и энергию W магнитного поля соленоида.

Решение: Индуктивность L связана с потокосцеплением Ψ и силой тока I

Потокосцепление можно выразить через поток и число витков N при плотном их прилегании друг к другу:

Из этих выражений индуктивность соленоида:

. (1)

Произведём вычисления:

.

Энергия W магнитного поля соленоида с индуктивностью L при силе тока I, протекающего по его обмотке, определяется соотношением:

.

Подставим в эту формулу соотношение (1) и произведем вычисления

.

.

1. В элементарной теории атома водорода принимают, что электрон обращается вокруг ядра по круговой орбите. Определить скорость электрона, если радиус орбиты 53 пм, а также частоту вращения электрона.

2. Два точечных заряда в воздухе на расстоянии 20 см друг от друга взаимодействуют с некоторой силой. На каком расстоянии нужно поместить эти заряды в масле с диэлектрической проницаемостью 5, чтобы получить ту же силу взаимодействия?

3. В вершинах квадрата со стороной 10 см находятся одинаковые заряды по 0.3 нКл каждый. Определить модуль и направление силы, действующей на один из зарядов со стороны трех других.

4. Два шарика, массой по 0.1 г каждый, подвешены в одной точке на нитях длиной 20 см каждая. Получив одинаковый заряд, шарики разошлись так, что нити образовали между собой угол 60⁰. Найти заряд каждого шарика.

5. Расстояние между двумя точечными зарядами 0.1 мкКл и –0.1 мкКл равно 10 см. Определить напряженность и потенциал точки, удалённый на 6 см от первого и на 8 см от второго заряда.

6. Заряды 1 мкКл и -1 мкКл находятся на расстоянии 10 см. Определить напряженность и потенциал поля в точке, удалённой на расстояние

10 см от первого заряда и лежащей на линии, проходящей через первый заряд перпендикулярно направлению от первого заряда ко второму.

7. Плоская квадратная пластина со стороной 10 см находится на некотором расстоянии от бесконечной равномерно заряженной плоскости с плотностью заряда 1 мкКл/м². Плоскость пластины составляет угол 30⁰ с линиями поля. Найти поток вектора напряженности через эту пластину.

8. В центре сферы радиуса 20 см находится точечный заряд 10 нКл. Определить поток вектора напряжённости через часть сферической поверхности площадью 20 см².

9. Плоская прямоугольная площадка со сторонами а и b, равными 3 и 2 см соответственно, находится на расстоянии 10 м от точечного заряда

1 мкКл. Площадка ориентирована так, что линии напряжённости составляют угол 30⁰ с её поверхностью. Найти поток вектора напряжённости через площадку.

10. К бесконечной равномерно заряженной вертикальной плоскости подвешен на нити одноимённо заряженный шарик массой 50 мг и зарядом 0.6 нКл. Сила натяжения нити, на которой висит шарик, 0.7 мН. Найти поверхностную плотность заряда на плоскости.

11. Бесконечная плоскость равномерно заряжена с поверхностной плотностью 4 нКл/м². Определить значение и направление градиента потенциала электрического поля, созданного этой плоскостью.

12. Электрическое поле создано положительным точечным зарядом. Потенциал поля в точке, удалённой от заряда на 12 см, равен 24 В. Определить значение и направление градиента потенциала в этой точке.

13. Металлический шарик диаметром 2 см заряжен отрицательно до потенциала 150 В. Сколько электронов находится на поверхности шарика?

14. Конденсаторы с электроемкостями C₁=0.2 мкФ, C₂=0.1мкФ, C₃=0.3 мкФ, C₄=0.4 мкФ соединены так, как показано на рис. Определить электроемкость батареи конденсаторов.

15. Пылинка массой 1 нг, несущая на себе пять электронов, прошла ускоряющую разность потенциалов 3 МВ в вакууме. Какова кинетическая энергия пылинки? Какую скорость приобрела пылинка?

16. Шару радиусом 10 см сообщен заряд 80 нКл, равномерно распределенный по поверхности шара. Определить энергию поля, созданного шаром в вакууме.

17. Определить среднюю скорость упорядоченного движения электронов в медном проводнике при силе тока 10 А и сечении проводника, равном 1 мм². Принять, что на каждый атом меди приходится два электрона проводимости. Плотность меди 8600 кг/м³.

18. Сила тока в металлическом проводнике равна 0.8 А, сечение проводника 4 мм². Принимая, что в каждом см³ металла содержится 2.510²² свободных электронов, определить среднюю скорость их упорядоченного движения.

19. При внешнем сопротивлении 3 Ом ток в цепи 0.3 А, а при внешнем сопротивлении 5 Ом ток равен 0.2 А. Определить ток короткого замыкания.

20. Элемент с ЭДС 1.6 В имеет внутреннее сопротивление 0.5 Ом. Найти КПД элемента при токе в цепи 2.4 А.

21. В медном проводнике длиной 2 м и площадью поперечного сечения 0.4 мм² течет ток. При этом ежесекундно выделяется количество теплоты 0.35 Дж. Сколько электронов проходит за 1 с через поперечное сечение проводника? Удельное сопротивление меди 1.710^-8 Омм.

22. Найти количество теплоты, выделяющейся ежесекундно в 1 см³ медного провода при плотности тока 30 А/см². Удельное сопротивление меди 1.710^-8 Омм.

23. Расстояние между двумя длинными параллельными проводами 0.05 м. По проводам в одном направлении текут одинаковые токи в 30 А каждый. Найти индукцию и напряженность магнитного поля в точке, находящейся на расстоянии 0.04 м от одного и 0.03 м от другого провода.

24. Два длинных прямолинейных проводника расположены параллельно на расстоянии 50 см друг от друга. В первом проводнике течет ток 20 А, во втором – 24 А. Определить напряженность магнитного поля в точке, расположенной на расстоянии 40 см от первого проводника и на расстоянии 30 см от второго, если токи в них направлены противоположно.

25. По двум бесконечно длинным прямым параллельным проводам текут токи силой 20 и 30 А в одном направлении. Расстояние между ними

10 см. Вычислить магнитную индукцию в точке, удаленной от обоих проводов на одинаковое расстояние 10 см.

26. Электрон в атоме водорода движется вокруг ядра по круговой орбите. Найти отношение магнитного момента эквивалентного кругового тока к моменту импульса орбитального движения электрона. Указать направления векторов магнитного момента и момента импульса.

27. По двум параллельным проводам длиной 1 м каждый текут токи одинаковой силы. Расстояние между проводами равно 0.01 м. Токи взаимодействуют с силой 110^-3 Н. Найти силу тока в проводах.

28. Вычислить радиус дуги окружности, которую описывает протон в магнитном поле с индукцией 1.510^-2 Тл, если скорость протона равна 210⁶ м/с.

29. Ион, несущий один элементарный заряд, движется в однородном магнитном поле с индукцией 0.015 Тл по окружности радиусом 0.1 м. Определить импульс иона.

30. Соленоид содержит 600 витков. При силе тока 10 А магнитный поток равен 8010^-6 Вб. Определить индуктивность соленоида и потокосцепление.

31. Соленоид индуктивностью 4.10^-3 Гн содержит 600 витков. Определить магнитный поток и потокосцепление, если сила тока, протекающего по обмотке, равна 12 А.

32. В однородном магнитном поле находится виток площадью 10 см², расположенный перпендикулярно силовым линиям. Какой ток потечет по витку, если поле будет убывать с постоянной скоростью 8 кА/(мс)? Сопротивление витка 1 Ом.

33. Прямой провод длиной 0.40 м движется в однородном магнитном поле со скоростью 5 м/с перпендикулярно линиям индукции. Разность потенциалов между концами провода 0.6 В. Вычислить индукцию магнитного поля.