Частные случаи условий трансверсальности

1. Если одна из граничных точек, например, правая перемещается по горизонтальной прямой 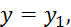то 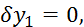и условие трансверсальности записываем как

(6)

2. Если задана абсцисса одного из концов, а граничное условие отсутствует, то это означает, что граничная точка может перемещаться по вертикальной прямой, например, 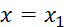. Тогда вместо условия трансверсальности записывают условие

Примеры решения задач

Задача 1.

Найти кривую минимальной длины, соединяющую параболу и прямую

Решение.

Функционалом в данном случае является длина дуги

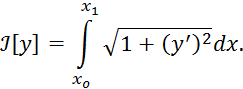
Пусть левая граничная точка перемещается по параболе а правая по прямой

Функция

Шаг 1. Составляем и решаем уравнение Эйлера:

Имеет место частный случай, когда функция F зависит только от

Тогда , а ;

Общее решение такого уравнения имеет вид

Заметим, что . (8)

Шаг 2. С учетом того, что искомая кривая и линии, по которым перемещаются граничные точки, должны пересекаться, получаем условие:

В данной задаче: ,

Шаг 3. Записываем условия трансверсальности

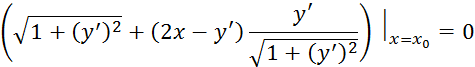
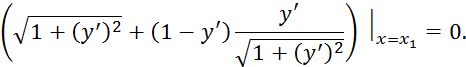
С учетом условия (8):

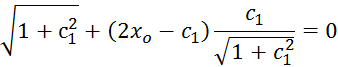
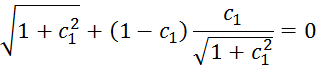
Шаг 4. Для определения решаем систему уравнений

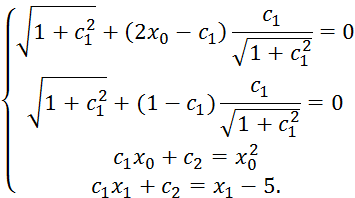
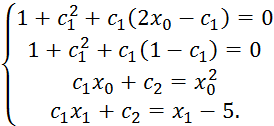
Вычитая из первого уравнения системы второе, получаем

.

Подставляя в третье уравнение системы, получаем соотношение между

Подстановка этого соотношения в первое уравнение системы дает:

Тогда Из четвертого уравнения системы получаем

Уравнение искомой кривой:

Расстояние между параболой и прямой:

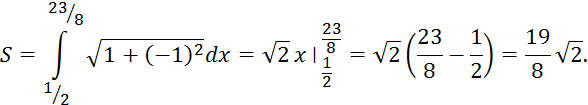
Задача2.

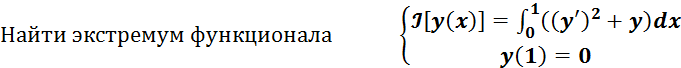
Поскольку отсутствует граничное условие для левой граничной точки, то принято считать, что левый конец движется по вертикальной линии. В этом случае граничное условие имеет вид:

Решая уравнение Эйлера, находим уравнение экстремали:

С учетом условий трансверсальности:

С учетом граничного условия получаем

Искомая кривая

ВАРИАНТЫ:

1. 

()

2. 

()

3. 

()

Ргр 11. Принцип максимума л.С. Понтрягина

Принцип наименьшего действия в механике.

Наиболее общей формой закона движения в механике является принцип наименьшего действия. Согласно этому принципу механическая система полностью задается координатами и скоростями (импульсами ) элементов системы при помощи функции Лагранжа , которая является разностью между кинетической и потенциальной энергиями системы. Движение между двумя точкамиивсегда происходит таким образом, чтобы функционал действия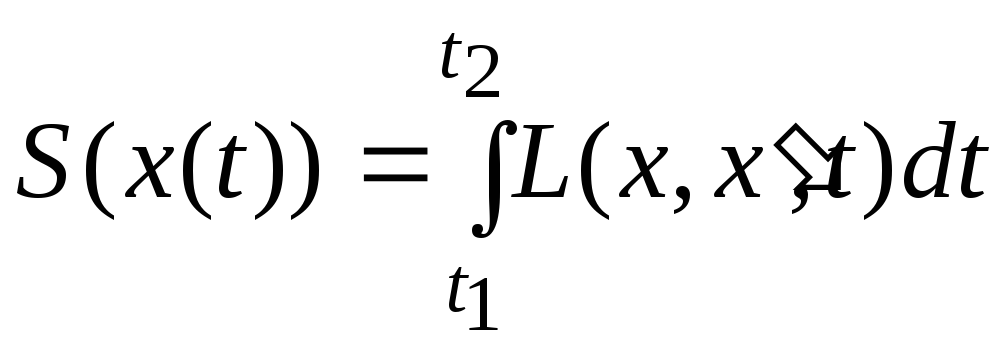принимал наименьшее возможное значение. Другими словами траектория движениядолжна быть экстремалью и удовлетворять уравнению Эйлера, которое в механике называют уравнением Лагранжа:.

Используя выражение для кинетической энергии, представляем функцию Лагранжа в виде . Тогда частная производная посовпадает с импульсом системы. А из уравнения Лагранжа следует, что. Пусть функция Лагранжа явно не зависит от времени. Тогда полную производную по времени записываем следующим образом:

.

Из последнего уравнения следует, что при движении по экстремали сохраняется постоянной величина (). Эта величина являетсяполной энергией системы и ее называют гамильтонианом системы .

Запишем выражение для полного дифференциала этой функции:

.

Сопоставляя полученное выражение с общим выражением для полного дифференциала

, получаем уравнения, которые в механике называют уравнениями Гамильтона

.

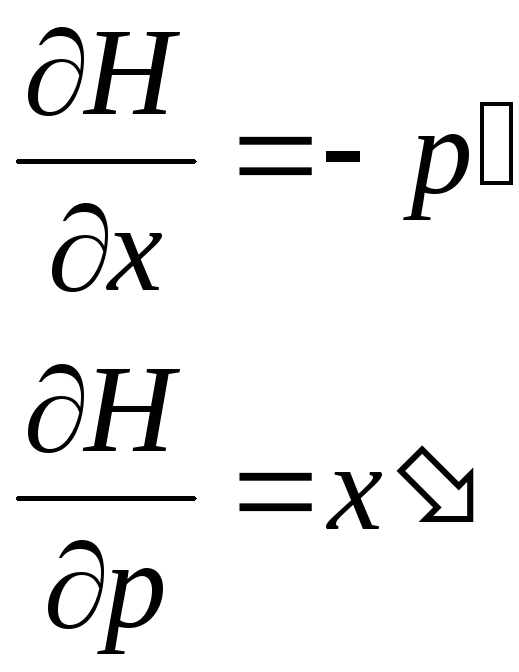Эти уравнения являются наиболее общей формой записи уравнений движения. Таким образом, если движение подчиняется уравнениям Гамильтона, то вдоль всей траектории энергия системы сохраняется.

1. Принцип максимума Л.С. Понтрягина в оптимальном управлении.

Пусть движение объекта задается системой дифференциальных уравнений

,

Здесь 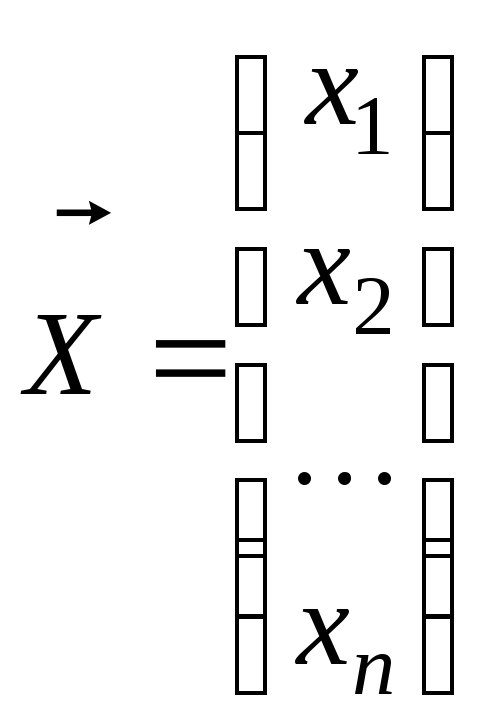- вектор фазовых координат, а - вектор управления. Важным является то, что вектор управления не может быть произвольным. Он ограничен физическими и конструкционными особенностями задачи : .

Задача. Требуется найти такую функцию управления , которая обеспечила бы минимум функционала

.

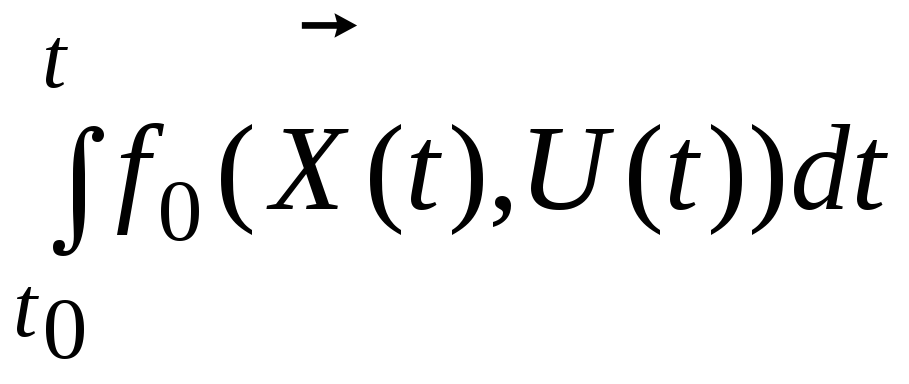Этот функционал может иметь различный смысл, например, может быть временем перехода системы из одного состояния в другое, временем затухания переходного процесса и т.д.

Рассмотрим линейную задачу на быстродействие. В этой задаче функционал имеет смысл времени перехода

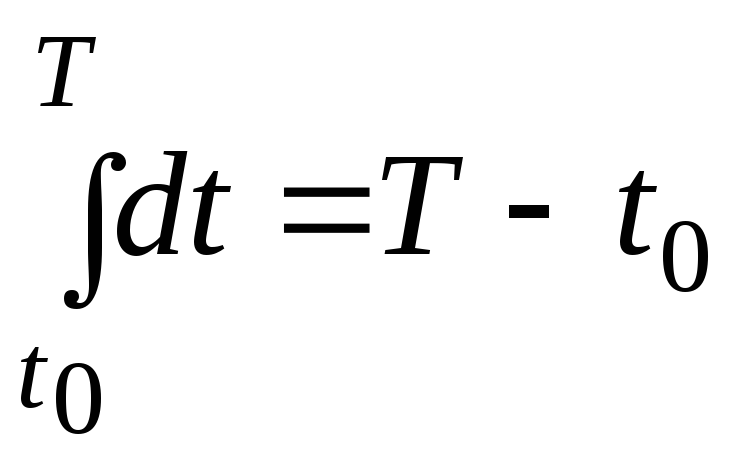
системы из состояния в состояние .

Оптимальным называют управление , которое обеспечит перевод системы из одного состояния в другое за наименьшее время.

Однако, ограниченность управления не позволяет применить для решения задачи классическое вариационное исчисление. Задачу решил Л.С. Понтрягин следующим образом.

Кроме фазовой координаты в рассмотрение вводится также и фазовый импульс. Обозначим вектор фазового импульса как .

По аналогии с классической теоретической механикой рассматривается функция

,

которая называется гамильтонианом и по смыслу является полной энергией системы. Эта функция связана с векторами фазовых координат и импульсов уравнениями, аналогичными уравнениям Гамильтона в механике

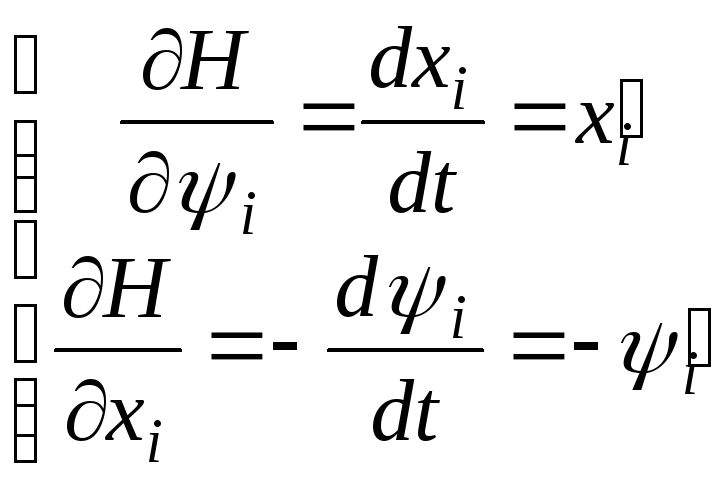
Для оптимального управления вектор управления должен быть таким, чтобы при любых фазовых координатах и импульсах обеспечивался максимум гамильтониана как функции управления .

При этом необходимые условия существования экстремума имеют вид

.

Запись линейной системы в матричной форме имеет вид

.

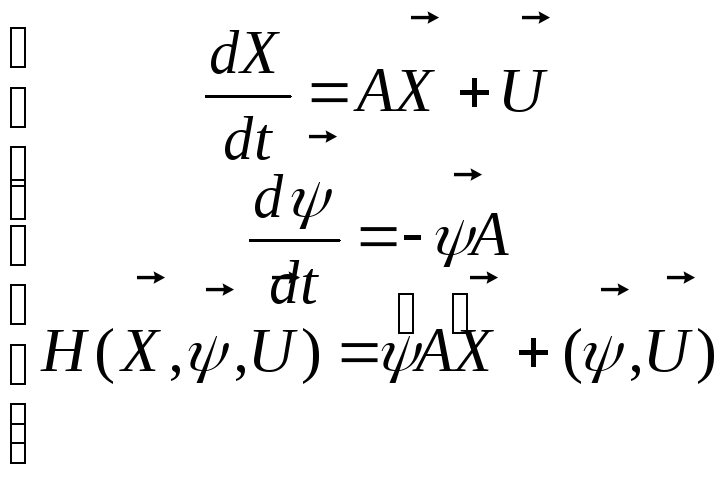Из последнего выражения гамильтониана следует, что он принимает наибольшее значение в случае, когда скалярное произведение максимально. Другими словами векторы фазового импульса и управления должны быть сонаправлены.

Рассмотрим конкретную задачу: точка массы движется по инерции. Как за наименьшее время остановить ее в начале координат под действием ограниченной силы?

Уравнение движения в данном случае имеет вид .

Шаг1. Переписываем дифференциальное уравнение в равносильную систему, вводя новые переменные

.

Записываем гамильтониан системы

Шаг 2. Записываем уравнения Гамильтона (второе уравнение из системы) и получаем систему уравнений для нахождения фазовых импульсов:

.

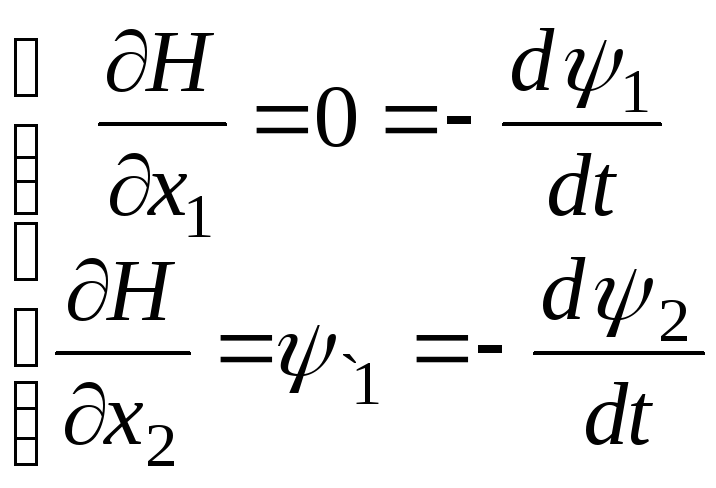Решение системы имеет вид .

Шаг 3. Найденные выражения для импульсов подставляем в гамильтониан системы

.

Записываем необходимые условия существования экстремума:

.

Из этого выражения видно, что производная имеет только один нуль. Функция является строго монотонной и изменяет знак один раз.

Максимум гамильтониана как функции управления обеспечивается при условии: управление принимает максимальное по абсолютной величине значение. Поэтому возможными значениями управления являются