1.1.5.3. Перпендикулярность прямой и плоскости

Перпендикулярность прямой и плоскости – особый случай пересечения прямой с плоскостью.

Прямая перпендикулярна плоскости в том случае, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости. В качестве пересекающихся прямых следует использовать горизонталь и фронталь плоскости. На основании теоремы о проецировании прямого угла горизонтальная проекция перпендикуляра проецируется перпендикулярно горизонтальной проекции горизонтали, а фронтальная проекция перпендикуляра – перпендикулярно фронтальной проекции фронтали.

На рис. 16 прямая l перпендикулярна плоскости заданной треугольником ABC. Следовательно, на фронтальной плоскости проекций П₂ фронтальная проекция прямой (l₂) перпендикулярна фронтальной проекции фронтали (f₂), а горизонтальная проекция прямой (l₁) перпендикулярна горизонтальной проекции горизонтали (h₁).

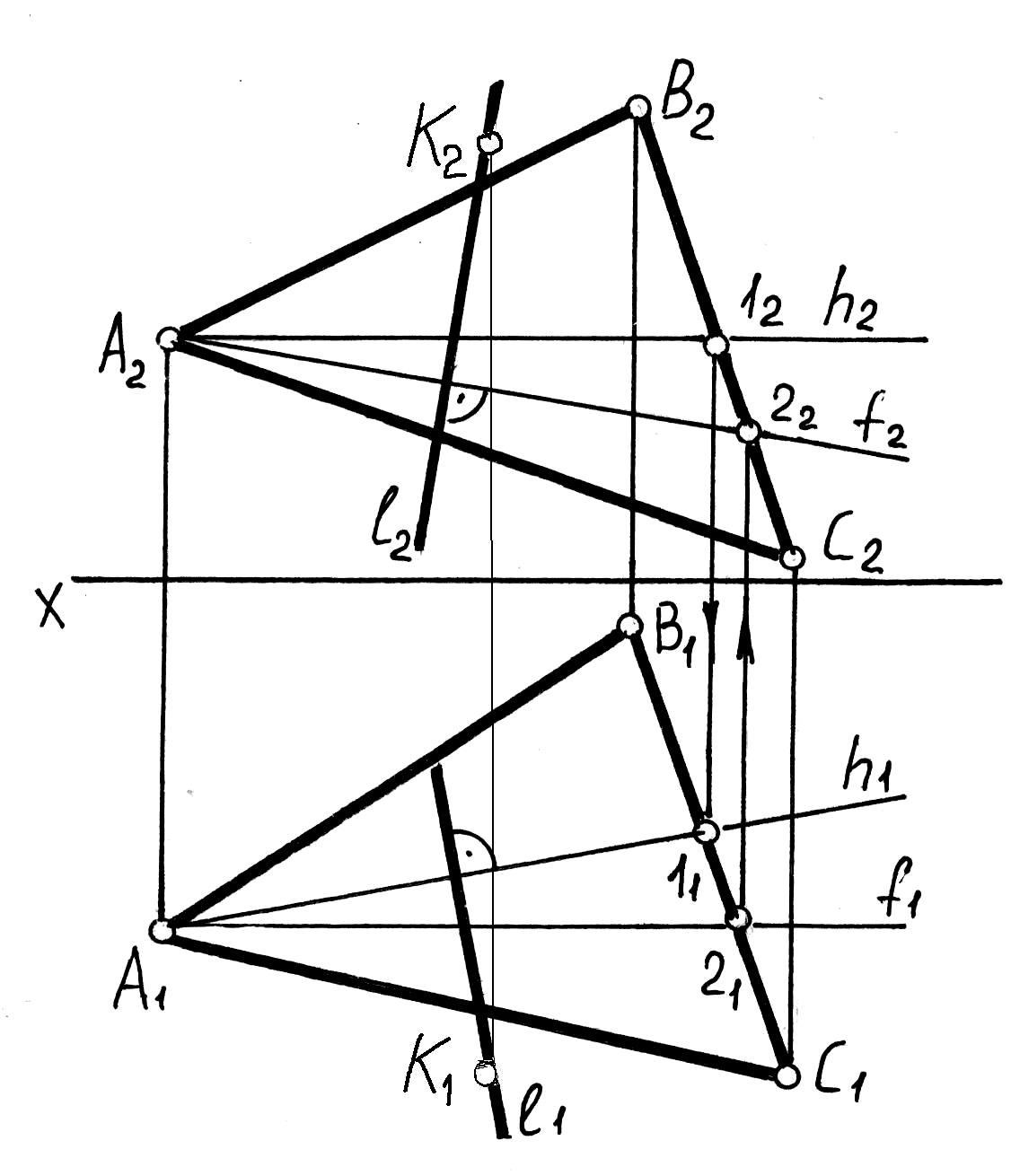
Рис. 16

1.2. Метрические задачи

Метрические задачи – это задачи, связанные с определением на комплексном чертеже истинных величин расстояний, углов и плоских фигур.

Первая группа задач включает в себя определение расстояний от точки до другой точки, от точки до прямой, до плоскости, поверхности.

Вторая группа задач включает в себя определение углов между пересекающимися (скрещивающимися) прямыми, между прямой и плоскостью, между двумя плоскостями.

Третья группа задач связана с определением натуральной величины плоской фигуры и части поверхности (развертка).

1.2.1. Определение расстояния от точки до плоскости

Определение расстояний от точки до плоскости в начертательной геометрии осуществляют на основании свойства перпендикулярности прямой и плоскости. Решение задачи распадается на три этапа:

1) в плоскости проводят горизонталь и фронталь (на рис. 17 плоскость задана горизонталью и фронталью);

2) из точки A опустить перпендикуляр l на плоскость

(l₂ ׀ f_2, l ₁ ׀ h₁);

3) определить точку K пересечения перпендикуляра l с плоскостью:

а) l є δ, δ ׀ П₂;

б) δ ∩  = [1-2];

в) [1-2] ∩ l = K.

4) методом прямоугольного треугольника определить натуральную величину отрезка AK (отрезок A^oK₂).

Если, наоборот, требуется найти точку L, удаленную от плоскости на определенное расстояние, то необходимо:

1) из точки A (рис. 18), расположенной в плоскости треугольника АВС, восставить перпендикуляр АМ произвольной длины (A₂M₂ ׀ f_{2 ,} А₁М₁ ׀ h₁);

2) методом прямоугольного треугольника найти натуральную величину перпендикуляра АМ (А₁М^o);

3) на натуральной величине A₁М^o от точки А₁ отложить отрезок A₁L^o = 30 мм и спроецировать точку L^o на проекции перпендикуляра (проекции A₁L₁ и A₂L₂).

Рис. 18

1.2.2. Перпендикулярность двух плоскостей

Две плоскости перпендикулярны, если одна из них содержит перпендикуляр к другой плоскости.

На рис. 19 плоскость β, заданная пересекающимися прямыми l и k, перпендикулярна плоскости a, заданной следами. Прямая l является перпендикуляром к плоскости a, а прямая k – прямой общего положения:

a ׀ β (l ∩ k ), т.к.: l ׀ a (l₁ ׀ h^o₁, l₂ ׀ f ^o₂).

2. Принятые обозначения

При составлении алгоритмов решения задач были использованы следующие символы, обозначающие отношения между геометрическими элементами:

є – принадлежит, является элементом;

∩ – пересечение;

׀׀ – параллельность;

׀ – перпендикулярность;

= – результат действия;

≡ – знак тождества.