Задание по ТВ

Для того, чтобы получить свои личные числовые данные, необходимо взять свой номер по списку (А – предпоследняя цифра, В – последняя) и выбрать из таблицы 1 параметр m, а из таблицы 2 параметр n. Эти два числа нужно подставить в условия задач.

Таблица 1 (выбор параметра m)

A	0	1	2	3	4	5	6	7	8	9
m	4	3	5	1	3	2	4	2	1	5

Таблица 2 (выбор параметра n)

B	0	1	2	3	4	5	6	7	8	9
m	3	2	1	4	5	3	1	5	2	4

Численная обработка данных одномерной выборки

Выборка Х объемом N=100 измерений задана таблицей

	5	13			19	10	3

где - результаты измерений, - частоты, с которыми встречаются значения , , .

1. Построить полигон относительных частот .

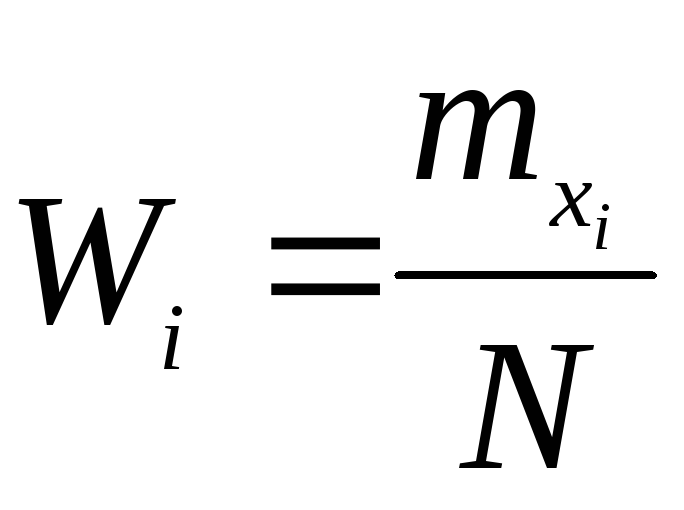2. Вычислить среднее выборочное 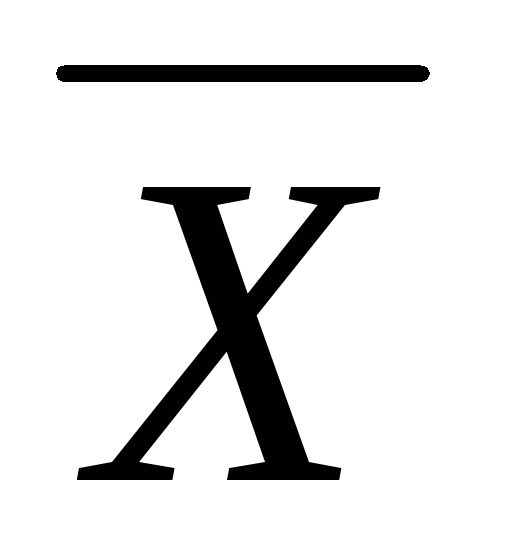, выборочную дисперсию и среднее квадратическое отклонение .

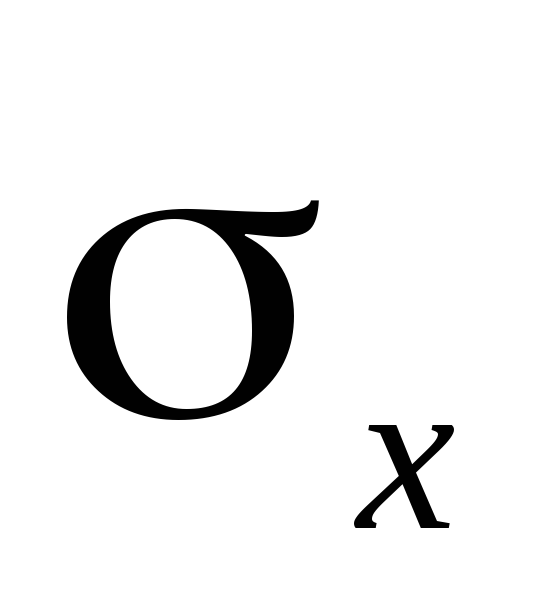3. По критерию 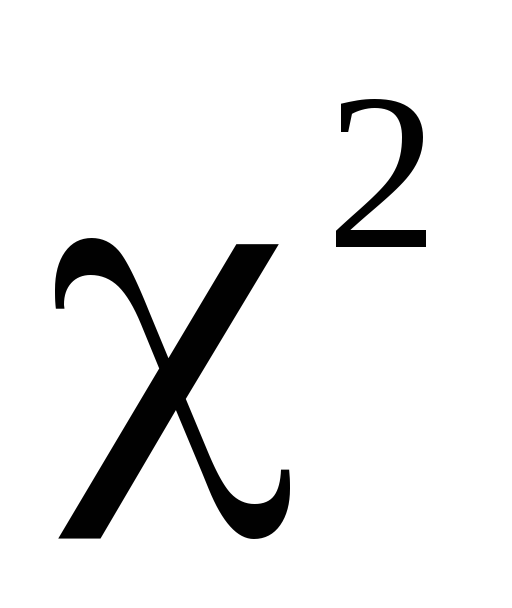проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости .

Примечание. Для расчетов и рекомендуется перейти к условным значениям и, взяв за ложный нуль значение с наибольшей частотой, использовать суммы и .

Построение уравнения прямой регрессии (пример)

Двумерная выборка результатов совместных измерений признаков х и у объемом N=100 измерений задана корреляционной таблицей:

	2	3	-	-	-	5
	3	8	2	-	-	13
	-			-	-
	-	-			-
	-	-	9	10	-	19
	-	-	3	6	1	10
	-	-	-	1	2	3
	5				3	N=100

где , .

1. Найти и 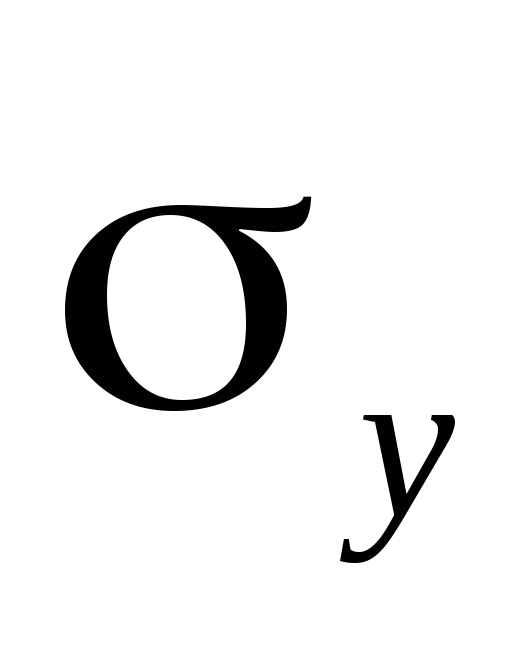для выборки

	5				3

(Расчеты и можно провести аналогично расчетам и в задании )

2. Построить уравнение прямой регрессии на 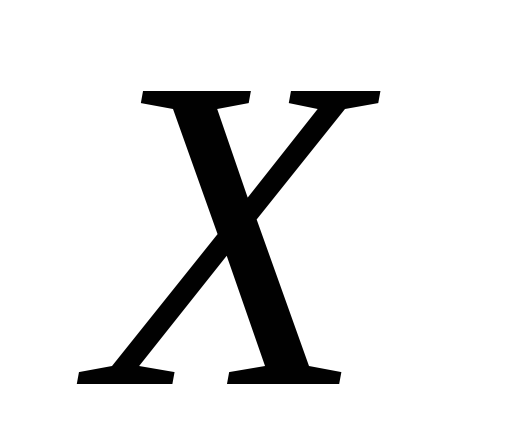в виде 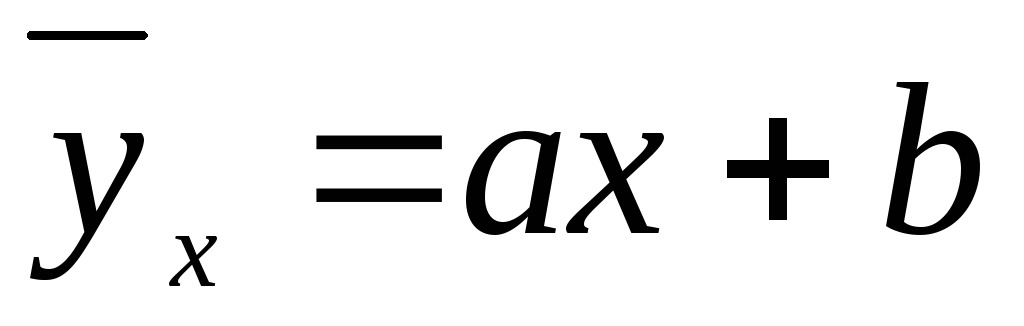, 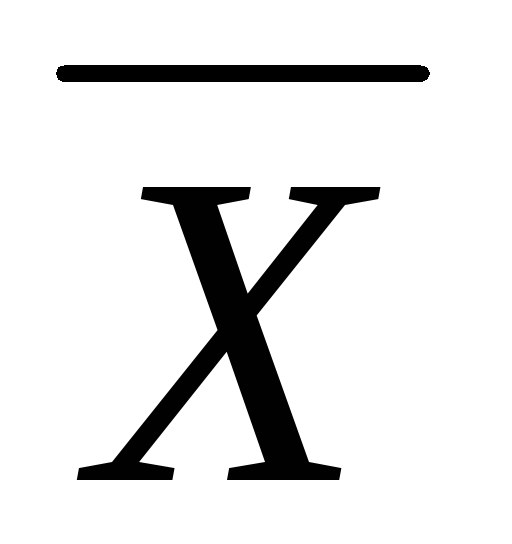и 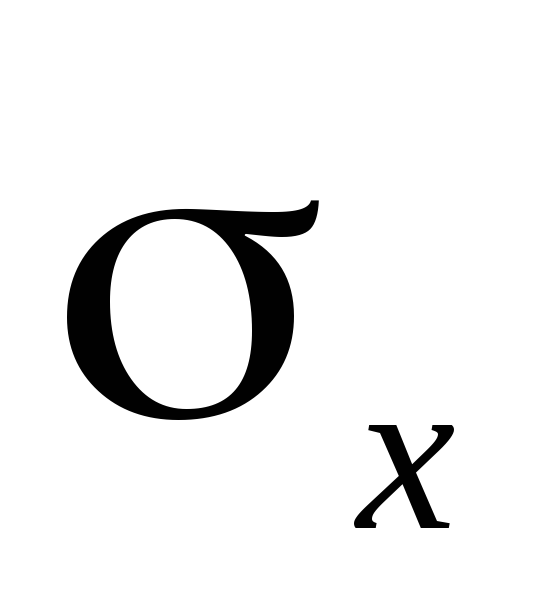следует взять из задачи …..

3. На графике изобразить корреляционное поле, то есть нанести точки и построить прямую .

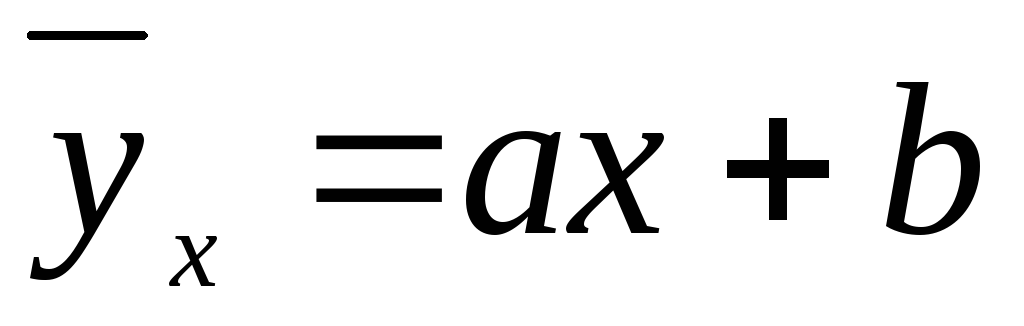Примечание. Уравнение регрессии сначала рекомендуется найти в виде , где - выборочный коэффициент корреляции, для расчета которого можно воспользоваться методом четырех полей.

2. Построение уравнения прямой регрессии

Двумерная выборка результатов совместных измерений признаков х и у объемом N=100 измерений задана корреляционной таблицей:

		1	2	3	4	5
		0,5	1,3	2,1	2,9	3,7
1	0,2	2	3				5
2	1,4	3	8	2			13
3	2,6		9	16			25
4	3,8			15	10		25
5	5			9	10		19
6	6,2			3	6	1	10
7	7,4				1	2	3
		5	20	45	27	3	N=100

1. Найти и 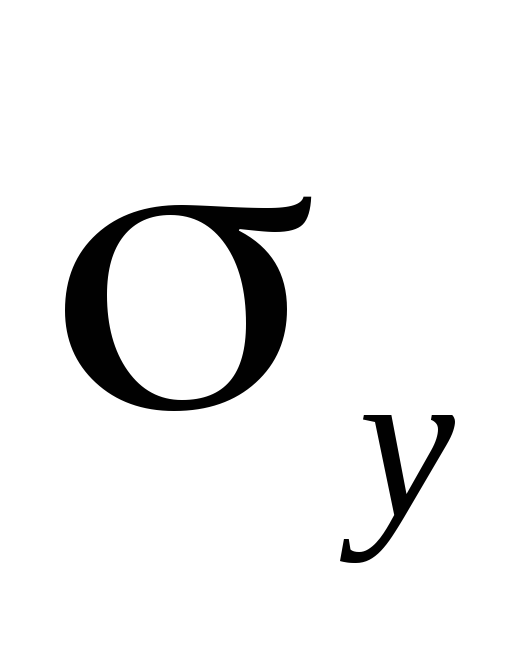для выборки

	0,5	1,3	2,1	2,9	3,7
	5	20	45	27	3

Решение. Для вычисления , и воспользуемся методом произведений. Введем условные варианты , где - значение , которому соответствует наибольшая частота, , - шаг выборки, .

Тогда, вычисляя , получим условный ряд:

			0	1	2
	5	20	45	27	3

Для этого ряда составим расчетную таблицу

1		5		20	5
2		20		20	0
3	0	45	0	0	45
4	1	27	27	27	108
5	2	3	6	12	27
		100	3	79	185

Проверка:

,

, .

Условные характеристики:

;

;

.

Возвращаясь к исходному вариационному ряду, с помощью равенств получаем

;

;

.

2. Построить уравнение прямой регрессии на в виде 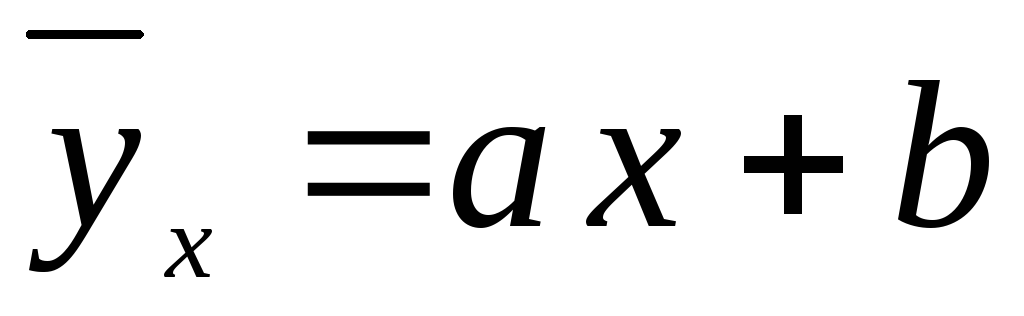. Уравнение прямой регрессии на 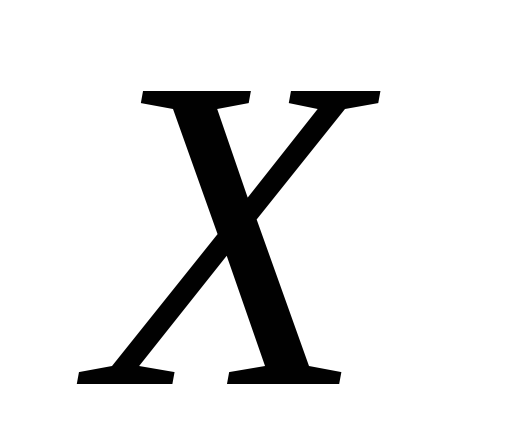имеет вид:

.

Значения и частоты их появления совпадают с данными для задачи….

Следовательно,

, .

Значения и найдены в задаче….: , .

Коэффициент корреляции определяется по формуле

,

где .

Для нахождения воспользуемся корреляционной таблицей

		1	2	3	4	5
		0,5	1,3	2,1	2,9	3,7
1	0,2	2	3				5	0,98
2	1,4	3	8	2			13	22,54
3	2,6		9	16			25	117,78
4	3,8		15	10			25	229,9
5	5			9	10		19	239,5
6	6,2			3	6	1	10	169,88
7	7,4				1	2	3	46,22
		5	20	45	27	3	N=100

Как следует из таблицы

Таким образом,

.

Уравнение прямой регрессии на имеет вид:

.

Подставляя численные значения, получаем:

.

3. На графике изобразить корреляционное поле и построить прямую .

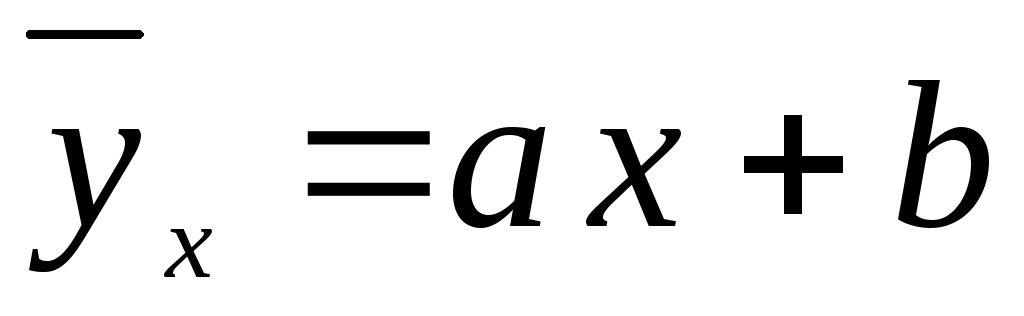Построим график прямой регрессии на .

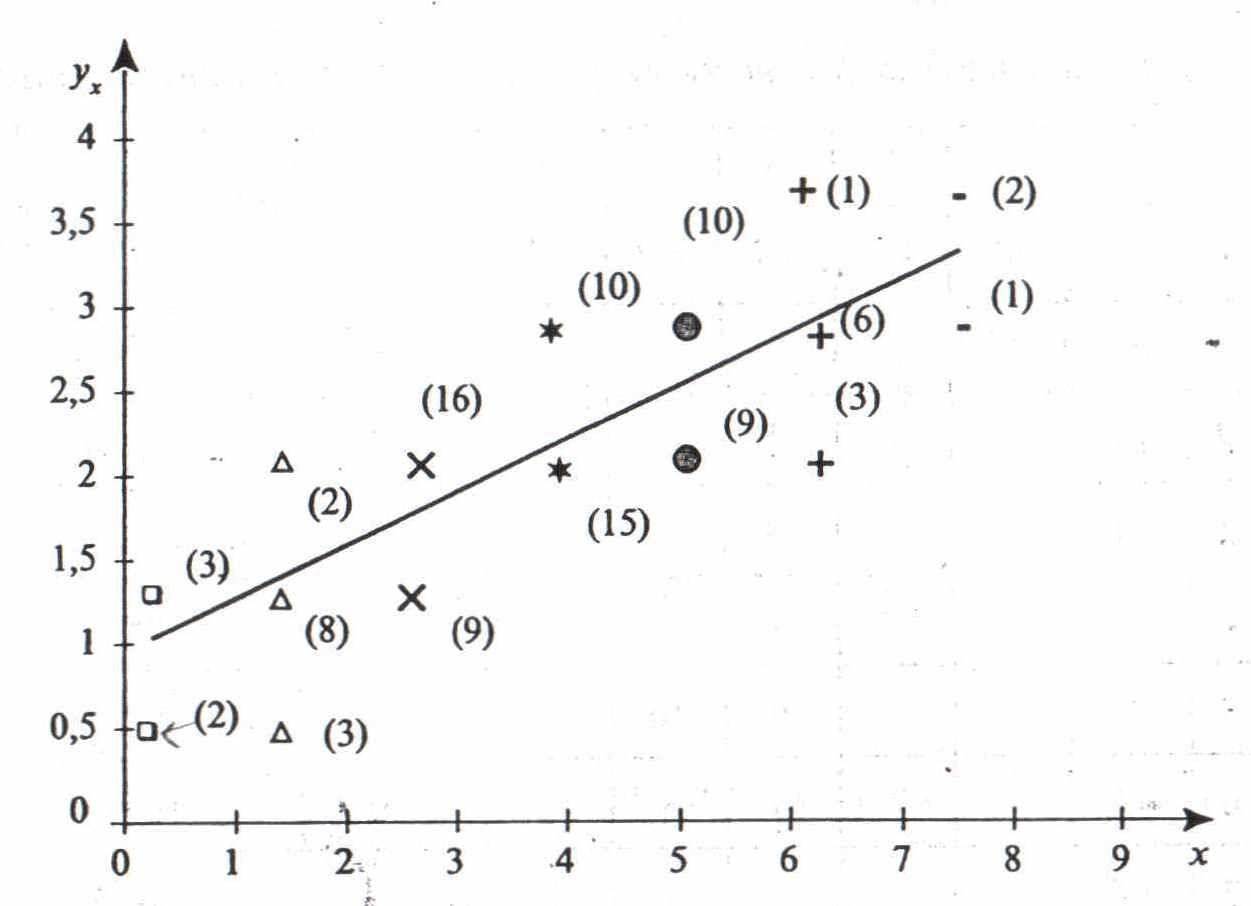
На графике радом с точками указаны частоты их появления.