Karmazin_-_Teoria_Igr_Uchebnik / P11_3

Тема 11. РЕШЕНИЕ ЗАДАЧИ О НАЗНАЧЕНИЯХ

Имеется лиц с номерами , способных выполнить работ с номерами . На выполнение -й работы -м лицом требуется единиц времени. Как следует распределить работы между людьми, чтобы минимизировать суммарное время их выполнения.

Пусть  время участия -го человека в выполнении -й работы. Все величины  неотрицательны, и, поскольку каждый человек должен быть полностью задействован, а каждое задание полностью выполнено, величина должна удовлетворять следующим ограничениям:

. (1)

(2)

При этих ограничениях надо минимизировать суммарное время выполнения всех работ

. (3)

Очевидно, что эта задача соответствует частному случаю транспортной задачи при . Так как все и  целые, то опорное решение задачи состоит из целочисленных значений , принимающих значения 0 или 1. Ранг системы ограничений равен , а любое опорное решение задачи содержит ровно ненулевых компонент . Следовательно, все опорные планы задачи о назначениях вырожденные.

Сведение задачи о назначениях к транспортной задаче с невырожденными опорными планами. Вместо задачи о назначениях рассмотрим транспортную задачу с объемами предложений: и объемами потребностей: . Все опорные планы такой транспортной задачи будут невырожденными. Решив эту транспортную задачу и положив затем , получим оптимальное решение задачи о назначениях.

Пример 1. Дана матрица  затрат времени работниками на выполнение каждого из пяти заданий:

.

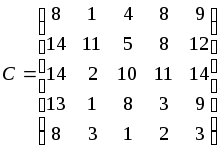Оптимальное назначение работников на выполнение заданий можно найти, решив следующую транспортную задачу:

Таблица 1

	1+		1+		1+		1+		1+
		8		1		4		8		9
1
		14		11		5		8		12
1
		14		2		10		11		14
1
		13		1		8		3		9
1
		8		3		1		2		3

Методы решения транспортной задачи описаны в десятом разделе.

Существует ряд методов решения задачи о назначениях, учитывающих конкретный вид ограничений (1), (2). Метод Мака наиболее простой из них.

Метод Мака для задачи о назначениях. В каждой строке матрицы затрат ищем минимальный элемент и подчеркиваем его. Если в матрице существуют строки, содержащие более одного минимального элемента, то в первую очередь следует подчеркивать минимальные элементы в строках с одним минимальным элементом. Затем в строках с несколькими минимальными элементами стараемся расставить подчеркивания так, чтобы в каждом столбце находился только один подчеркнутый элемент. Если удалось расставить подчеркивания так, что в каждом столбце присутствует ровно один подчеркнутый элемент, то задача решена: полагаем для подчеркнутых элементов, и для остальных элементов - это и будет оптимальный план назначений работников на задания.

Шаг 1. Отмечаем знаком «+» столбцы, содержащие более одного подчеркнутого элемента.

Шаг 2. Просматриваем строки, содержащие подчеркнутые элементы в столбцах, отмеченных знаком «+», и вычисляем

,

где  подчеркнутый элемент -й строки, находящийся среди столбцов отмеченных знаком «+», а  наименьший из элементов -й строки, находящихся в столбцах, не отмеченных знаком «+». Пусть .

Шаг 3. Увеличиваем все элементы столбцов, отмеченных знаком «+», на . Отмечаем штрихом элемент . Если таких элементов несколько, то отмечаем все.

Шаг 4. Столбцы, содержащие подчеркнутый и штрихованный элементы, отмечаем знаком «+». Если есть столбец, содержащий только штрихованный элемент, то переходим к следующему шагу. В противном случае переходим к шагу 2.

Шаг 5. В столбце, содержащем только штрихованный элемент, подчеркиваем этот элемент и убираем штрих. Это  новый подчеркнутый элемент. Находим исходный подчеркнутый элемент в той же строке, в которой находился штрихованный элемент, и убираем подчеркивание. Обозначим столбец, в котором находился этот подчеркнутый элемент, через .

Шаг 6. Если не содержит подчеркнутых элементов, то он должен содержать штрихованный элемент, возвращаемся в этом случае к шагу 5.

Шаг 7. Если есть еще столбцы без подчеркнутых элементов, то убираем все пометки кроме подчеркиваний и переходим к шагу 1. Если в каждом столбце имеется подчеркнутый элемент, работа алгоритма закончена.

Пример 2. Решим методом Мака задачу о назначениях с матрицей затрат из примера 1. На предварительном этапе отыскиваем минимальный элемент каждой строки и подчеркиваем его. Результат этой операции виден из табл.2. Есть столбцы, не содержащие подчеркнутых элементов, поэтому переходим к шагу 1: отмечаем знаком «+» столбцы 2 и 3. Шаг 2  находим , . Шаг 3  увеличиваем на элементы столбцов 2 и 3, отмечаем штрихом элемент, равный 2, в 5-й строке.

Таблица 2. Шаги 1 и 2 Таблица 3. Шаг 3

На 4-м шаге видим, что столбец 4 содержит только штрихованный элемент  переходим к следующему шагу. Шаг 5  подчеркиваем штрихованный элемент в 4-м столбце и убираем подчеркивание элемента 5-й строки и 4-го столбца. Шаг 6  4-й столбец () содержит подчеркнутый элемент, поэтому переходим к следующему шагу. На 7-м шаге видим, что в преобразованной таблице столбцы 1 и 5 не содержат подчеркнутых элементов, т.е. решение еще не найдено, переходим к шагу 1.

В табл. 5  13 представлены результаты пошагового выполнения следующих двух итераций.

Таблица 4. Шаги 4-7 Таблица 5. Шаги 1 и 2

Таблица 6. Шаги 3,4,2 Таблица 7. Шаги 3,4,2

Таблица 8. Шаги 36 Таблица 9. Шаги 5,6

Таблица 10. Шаги 5-7 Таблица 11. Шаги 1,2

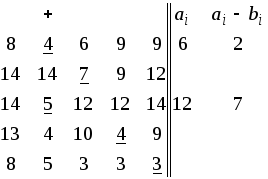
Таблица 12. Шаги 3,4,2 Таблица 13. Шаги 37

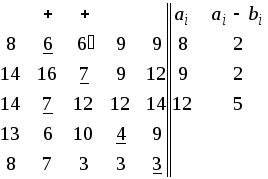
В результате получаем оптимальный план назначения работников на задания:

Время выполнения работ составит: .

Задание. В задачах 11.1  11.104 для пяти работников и пяти видов работ заданы матрицы затрат на выполнение каждым работником всех видов работ. Найти оптимальный план назначений на работы.

11.1 C=				11.2 C=
11.3 C=				11.4 C=
11.5 C=			11.6 C=

11.7 C=		11.8 C=
11.9 C=		11.10 C=
11.11 C=		11.12 C=
11.13 C=		11.14 C=
11.15 C=		11.16 C=
11.17 C=		11.18 C=
11.19 C=		11.20 C=
11.21 C=		11.22 C=
11.23 C=		11.24 C=
11.25 C=		11.26 C=
11.27 C=		11.28 C=
11.29 C=		11.30 C=
11.31 C=		11.32 C=
11.33 C=		11.34 C=
11.35 C=		11.36 C=
11.37 C=		11.38 C=
11.39 C=		11.40 C=
11.41 C=		11.42 C=
11.43 C=		11.44 C=
11.45 C=		11.46 C=
11.47 C=		11.48 C=
11.49 C=		11.50 C=
11.51 C=		11.52 C=
11.53 C=		11.54 C=
11.55 C=		11.56 C=
11.57 C=		11.58 C=
11.59 C=		11.60 C=
11.61 C=		11.62 C=
11.63 C=		11.64 C=
11.65 C=		11.66 C=
11.67 C=		11.68 C=
11.69 C=		11.70 C=
11.71 C=		11.72 C=
11.73 C=		11.74 C=
11.75 C=		11.76 C=
11.77 C=		11.78 C=
11.79 C=		11.80 C=
11.81 C=		11.82 C=
11.83 C=		11.84 C=
11.85 C=		11.86 C=
11.87 C=		11.88 C=
11.89 C=		11.90 C=
11.91 C=		11.92 C=
11.93 C=		11.94 C=
11.95 C=		11.96 C=
11.97 C=		11.98 C=
11.99 C=		11.100 C=
11.101 C=		11.102 C=
11.103 C=.		11.104 C=.

144