15. Ряды Фурье в гильбертовом пространстве. Равенство Парсеваля.

Ги́льбертово простра́нство — особый тип банаховых пространств, обобщение евклидова пространстванабесконечномерныйслучай. При этом гильбертово пространство не обязательно является бесконечномерным.

Гильбертово пространство есть банахово пространство,нормакоторого порождена положительно определённымскалярным произведением.

Ряды Фурье в гильбертовом пространстве

Пусть даны ортогональная система в Гильбертовом пространствеR и f — произвольный элемент из R. Предположим, мы хотим представить f в виде (бесконечной) линейной комбинации элементов :

Домножим это выражение на . С учётом ортогональности системы функций все слагаемые ряда обращаются в ноль, кроме слагаемого при n = k:

Последовательность чисел

называется координатами, или коэффициентами Фурье элемента f по системе , а ряд

называется рядом Фурье элемента f по ортогональной системе .

Ряд Фурье любого элемента f по любой ортогональной системе сходится в пространстве R, но его сумма не обязательно равна f. Для ортонормированной системы в сепарабельномгильбертовом пространстве следующие условия эквивалентны:

• система является базисом, то есть сумма ряда Фурье любого элемента равна этому элементу.

• система является полной, то есть в R не существует ненулевого элемента, ортогонального всем элементам 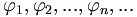одновременно.

• система является замкнутой, то есть для любого 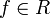выполнено равенство Парсеваля

.

• линейные комбинации элементов 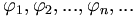плотныв пространстве R.

Если эти условия не выполняются, то сумма ряда Фурье элемента f равна его ортогональной проекцииназамыканиелинейной оболочкиэлементов . В этом случае вместо равенства Парсеваля справедливо неравенство Бесселя:

Ра́венство Парсева́ля — это аналог теоремы Пифагорав векторных пространствах соскалярным произведением. Названо по аналогии стеоремойдляпериодических функций, сформулированойПарсевалемв1799году.

Формулировка

Пусть дано гильбертово пространство , где — скалярное произведение, определённое на множествеH. Обозначим индуцированную этим скалярным произведением норму. Тогда если — ортонормированный базисв H, то

16. Сочетания и размещения

Основные правила комбинаторики.

Правило птичьих гнезд. Если имеется n+1 птиц, которых необходимо разместить в n гнездах, то при любом способе размещения хотя бы в одном гнезде окажутся не менее двух птиц.

Правило умножения. Пусть необходимо строить различные n-элементные последовательности a₁,.., a_n, для которых выполнены условия:

А) первый элемент может быть выбран m₁ способами;

Б) если i<n, то для каждого способа выбора значений первых I элементов последовательности значение i+1-го элемента может быть выбрано m_i+1 способами.

Тогда число различных последовательностей a₁, .., a_n равно: m₁m₂ . . . m_n.

Правило сложения. Пусть заданы непересекающиеся конечные множества A₁, .. A_k. Тогда мощность объединения этих множеств может быть определена по формуле: .

Размещения и сочетания

Пусть A – конечное множество, содержащее n элементов.

Размещениями из n элементов по m элементов множества D называются m-элементные последовательности, каждый член которых является элементом D.

Здесь предполагается, что m>=0. При этом, если m = 0, то соответствующее размещение не содержит ни одного элемента и является пустым.

Если множество A неизвестно или не уточняется, то говорят о размещении из n по m.

Размещение называется размещением без повторений, если все входящие в него элементы являются разными. В этом случае должно выполняться m<=n.

Число размещений из n по m без повторений обозначается как . И.

Объясняется так: n(n-1)*… *(n-m+1). Очевидно, что выбрать первый элемент можно n способами. Следующий элемент – на один меньше. И так далее до элемента под номером m. По правилу умножения число таких размещений равно (n-1)*… *(n-m+1).

Число размещений с повторениями:

Частный случай: Размещение без повторений всех элементов множества - число перестановок элементов произвольного n элементного множества. Обозначается как и равноn!.

Сочетанием из m по n называется всякая совокупность, состоящая из m элементов некоторого n-элементного множества.

Отличие от размещений: важен только состав, порядок не интересует.

Сочетания так же бывают без повторений и с повторениями.

Обозначим число сочетаний из n по m без повторений как . Тогда Справедливо следующее соотношение:

Объясняется так: Одно сочетание порождает m! размещений ( перестановка ).

.

Объясняется так:

Сочетания с повторами будем представлять в виде двоичных последовательностей длины n+m-1, составленных из m нулей и n единиц.

Например, если в сочетании 3 повтора первого элемента множества, то начало для него будет 0001. Т.е. для каждого элемента выстраиваем последовательности нулей и показываем конец с помощью единицы ( кроме последнего элемента. Ему не нужно ставить единицу в конце )

Например, Если A = {a1, a2, a3, a4}, то сочетание с повторениями, содержащее 2 элемента a1, 3 элемента a2 и 2 элемента a4 представляем так: (0010001100).

Таким образом задача сводится к подсчету количества вариантов расстановки n-1 единиц ( вместо нулей ) в последовательности нулей длины n+m-1. Это есть выбор n позиций из n+m-1. То есть .