
- •2. Случайные величины. Свойства функции распределения.
- •3. Распределение случайных дискретных величин
- •4. Формулы полной вероятности. Формула Байеса
- •5. Симплекс-метод
- •Симплекс-алгоритм
- •7. Необходимое условие условного минимума. Теорема Куна-Таккера.
- •Построение общего решения однородного уравнения
- •Нахождение частного решения неоднородного уравнения методом неопределенных коэффициентов
- •1) Нерезонансный случай.
- •2) Резонансный случай.
- •10. Краевые задачи. (Альтернатива Фредгольма. Функция Грина и её свойства. Теорема о свойствах собственных значений и собственных функций).
- •Функция Грина и её свойства.
- •11. Условный экстремум. Метод множителей Лагранжа
- •12. Формула Тейлора
- •13. Теорема Абеля о сходимости степенного ряда.
- •14. Принцип сжимающих отображений.
- •15. Ряды Фурье в гильбертовом пространстве. Равенство Парсеваля.
- •16. Сочетания и размещения
- •17. Минимизация днф.
- •18. Отношения эквивалентности и порядка.
- •19. Пути и циклы в графах
- •20. Задача Коши для одномерного волнового уравнения. Формула д’Аламбера
- •21. Гармонические функции. Постановка краевых задач для уравнения Лапласа и Пуассона.
- •22. Квадратичные формы. Закон инерции квадратичных форм. Критерий Сильвестра.
- •23. Собственные векторы и собственные значения линейного оператора.
- •24. Евклидово пространство. Ортогональность. Процесс ортогонализации.
- •25. Жорданова форма линейного оператора
- •26. Численные методы решения систем линейных алгебраических уравнений.
- •Метод Гаусса
Функция Грина и её свойства.
Если
непрерывная в квадрате [0;1]x[0;1]
функция G(t,s)
такая, что при любой
![]()
решение задачи (1)(2) представимо в виде (3), то функция G(t,s) называется функцией Грина краевой задачи (1)(2).
(1)(2) 
(3) ![]()
Теорема:
Если однородная краевая задача (1)(2)
имеет только нулевое решение, то
существует непрерывная в квадрате
[0;1]x[0;1]
функция
![]() ,
такая что любое решение неоднородной
краевой задачи (1)(2) представимо в виде
(3) – функция Грина.
,
такая что любое решение неоднородной
краевой задачи (1)(2) представимо в виде
(3) – функция Грина.
Доказательство:
Пусть однородная краевая задача (1)(2)
имеет только нулевое решение. Покажем,
что тогда найдется непрерывная в квадрате
[0;1]x[0;1]
функция
![]() ,
такая что любое решение неоднородной
краевой задачи (1)(2) представимо в виде
(3).
,
такая что любое решение неоднородной
краевой задачи (1)(2) представимо в виде
(3).
Действительно,
в этом случае в силу альтернативы
Фредгольма неоднородная краевая задача
(1)(2) разрешима при любой правой части
![]() и решение представимо в виде:
и решение представимо в виде:
(4) ![]() ,
,
где
![]() и
и![]() - решения задач Коши (1*) и (2*).
- решения задач Коши (1*) и (2*).
(1*) 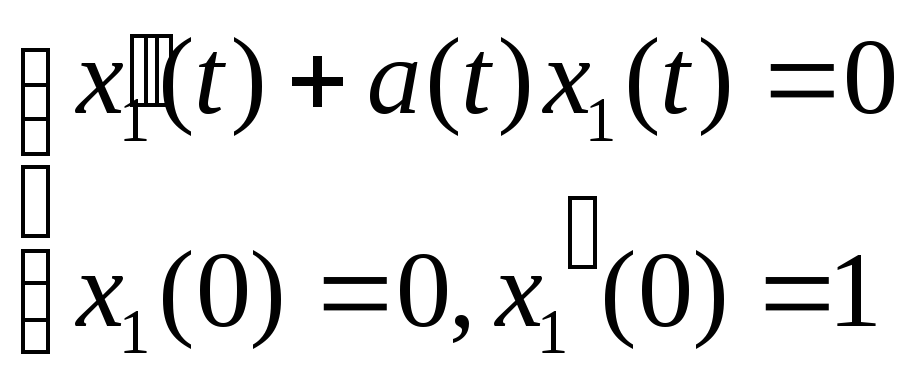
(2*) 
Преобразуем представление (4):
![]()
(**) ![]()
Введем функцию:

Очевидно,
что функция
![]() непрерывна
в квадрате [0;1]x[0;1]
(т.к.
непрерывна
в квадрате [0;1]x[0;1]
(т.к.
![]() и
и![]() непрерывные функции, а
непрерывные функции, а![]() – определитель Вронского, являющийся
константой).
– определитель Вронского, являющийся
константой).
![]()
Тогда из (**) получим:
![]() ,
чтд.
,
чтд.
Свойства функции Грина:
При каждом фиксированном s функция
 ,
как функция
,
как функция (
( )
при
)
при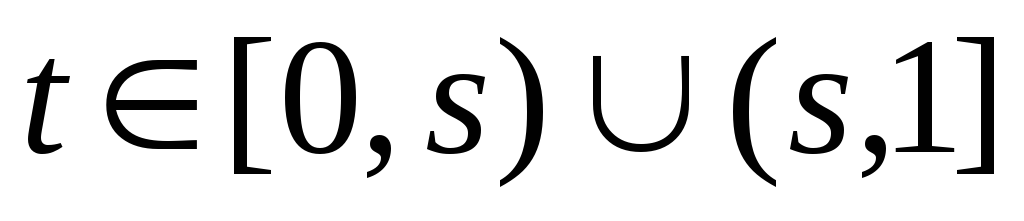 является решением однородного д.у.:
является решением однородного д.у.: .
Это следует из того, что
.
Это следует из того, что и
и - решения однородного уравнения.
- решения однородного уравнения.При каждом фиксированном s функция
 ,
как функция
,
как функция (
( )
при
)
при удовлетворяет однородным граничным
условиям (2) (следует из того, что
удовлетворяет однородным граничным
условиям (2) (следует из того, что ).
). непрерывна в
квадрате [0;1]x[0;1],
а её производная испытывает скачек,
равный 1.
непрерывна в
квадрате [0;1]x[0;1],
а её производная испытывает скачек,
равный 1.
![]() или
или![]()
Доказательство:
![]() (при
(при
![]() )
=
)
=![]()
![]() (при
(при
![]() )
=
)
=![]()
Тогда
![]() ,(
т.к.
,(
т.к.![]() ).
Чтд.
).
Чтд.
Утверждение.
Если функция ![]() удовлетворяет свойствам 1), 2), 3), то
удовлетворяет свойствам 1), 2), 3), то ![]() является функцией
Грина задачи (1)(2). Задача (1)(2) имеет
единственную функцию Грина.
является функцией
Грина задачи (1)(2). Задача (1)(2) имеет
единственную функцию Грина.
Теорема о свойствах собственных значений и собственных функций.
![]()
(1)(2)  ,
,![]()
Встает вопрос о существовании ненулевых решений этой задачи.
Значение
параметра
![]() ,
при котором задача (1)(2) имеет ненулевые
решения, называется собственным
значением, а соответствующее ненулевое
решение – собственной функцией задачи
(1)(2), принадлежащей собственному значению.
,
при котором задача (1)(2) имеет ненулевые
решения, называется собственным
значением, а соответствующее ненулевое
решение – собственной функцией задачи
(1)(2), принадлежащей собственному значению.
Задачи на собственные значения называются спектральными задачами.
Задача (1)(2) называется спектральной задачей Штурма-Лиувилля.
Множество всех собственных значений называется спектром задачи (1)(2).
Теорема о свойствах собственных значений и собственных функций: Краевая задача (1)(2) имеет бесконечное множество собственных значений, причем на каждом конечном интервале их не больше конечного числа. Собственные функции, соответствующие различным собственным значениям, ортогональны, а соответствующие одному собственному значению – пропорциональны.
Замечание: Все собственные значения задачи (1)(2) вещественны.
11. Условный экстремум. Метод множителей Лагранжа
Рассмотрим вопрос
об экстремуме функции
![]() при
условии, что
при
условии, что![]() и
и![]() связаны
соотношением
связаны
соотношением![]() .
Эта задача называетсязадачей
на условный экстремум.
Геометрически это означает, что мы
сравниваем между собой значения функции
.
Эта задача называетсязадачей
на условный экстремум.
Геометрически это означает, что мы
сравниваем между собой значения функции
![]() не
на всех точках области определения
функции, а лишь в тех, которые лежат на
кривой, определяемой уравнением
не
на всех точках области определения
функции, а лишь в тех, которые лежат на
кривой, определяемой уравнением![]() .
.
Предположим, что
уравнение
![]() определяет
некоторую функцию
определяет
некоторую функцию![]() ,
заданную неявно. Подставим ее в функцию
,
заданную неявно. Подставим ее в функцию![]() ,
получим
,
получим![]() .
.
Найдем теперь
экстремум функции
![]() .
.
![]() -необходимое
условие экстремума.
-необходимое
условие экстремума.
Производная неявной
функции
![]() .
.
Тогда необходимое
условие примет вид
![]() или
или![]() .
.
Обозначим это
соотношение через
![]() ,
получим, что в точке экстремума должны
выполняться условия
,
получим, что в точке экстремума должны
выполняться условия![]() и
и![]() (1).
(1).
Величину
![]() называюмножителем
Лагранжа.
Введем в рассмотрение функцию
Лагранжа.
называюмножителем
Лагранжа.
Введем в рассмотрение функцию
Лагранжа.
![]() .Тогда условия
(1) можно записать так
.Тогда условия
(1) можно записать так

А это необходимые
условия безусловного экстремума функции
![]() .
.
Таким образом
исходная задача на условный экстремум
заменена эквивалентной задачей на
безусловный экстремум для функции
Лагранжа исходной задачи. Из уравнений
(3) находят стационарные точки
![]() .
.
Перейдем теперь
к общему случаю. Будем искать локальный
экстремум функции
![]() при условии, что
при условии, что![]() .
.
Предположи, что
задача (5), (6) имеет локальный экстремум
в точке
![]() ,
и что функции ограничений (6) удовлетворяют
условию Якоби, т.е. в точке
,
и что функции ограничений (6) удовлетворяют
условию Якоби, т.е. в точке![]() ранг
матрицы Якоби, матрицы частных производных
функций ограничений, совпадает с числом
строк матрицы
ранг
матрицы Якоби, матрицы частных производных
функций ограничений, совпадает с числом
строк матрицы
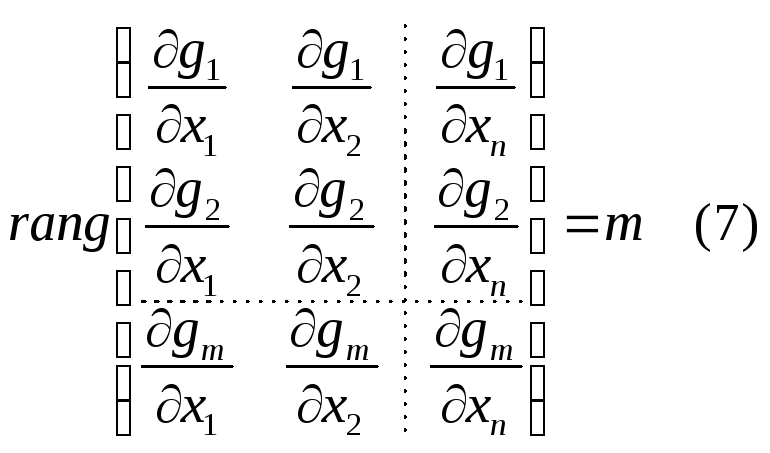
Рассуждая так же,
как в случае функции двух переменных
,получим необходимые условия которым
должны удовлетворять координаты точки
![]() .
Эти условия можно получить используя
функцию Лагранжа.
.
Эти условия можно получить используя
функцию Лагранжа.
Построим функцию Лагранжа для (5),(6).
![]() .
.
Эта функция зависит
от
![]() переменных.
В точке экстремума все ее частные
производные должны равняться нулю.
переменных.
В точке экстремума все ее частные
производные должны равняться нулю.
 .
.
Вопрос о нахождении стационарных точек функции (5) при наличии связей (6) свелся к решению системы (9), (10).
Точки локального
условного экстремума находятся среди
стационарных точек. Выяснение вопроса
о том, будет ли на самом деле стационарная
точка
![]() точкой условного экстремума, требует
исследование знака
точкой условного экстремума, требует
исследование знака![]() ,
если функции
,
если функции![]() и
и![]() дважды
непрерывно дифференцируемы. При выяснении
знака
дважды
непрерывно дифференцируемы. При выяснении
знака![]() нужно
учитывать, что дифференциалы
нужно
учитывать, что дифференциалы![]() удовлетворяют
уравнениям
удовлетворяют
уравнениям![]() .
.
Алгоритм решения задачи (5),(6).
Составляем функцию Лагранжа
 .
.Записываем необходимые условия экстремума
 .
.Решаем систему, находим стационарные точки функции
 ,
, .
.Для найденных стационарных точек проверяем достаточные условия экстремума.
Записываем выражение для второго дифференциала функции Лагранжа в точке
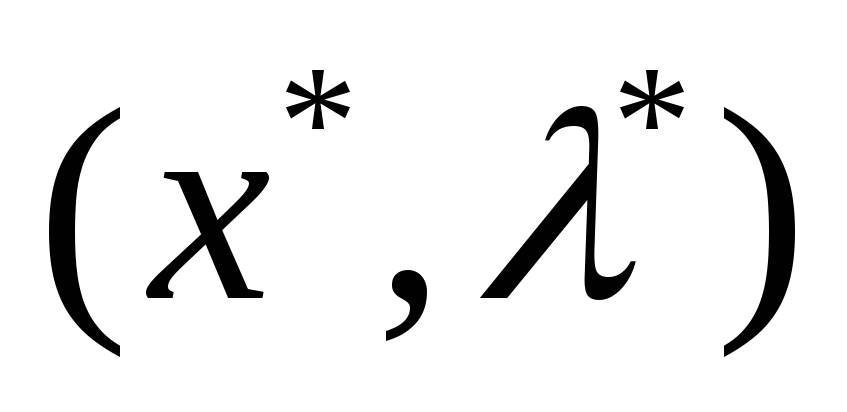 .
. .
.Запишем связи дифференциалов

 .
Если функции
.
Если функции удовлетворяют в точке
удовлетворяют в точке условию Якоби, то из этой системы
выразим
условию Якоби, то из этой системы
выразим дифференциалов
дифференциалов через остальные
через остальные и представим
и представим .
.Если
 при ненулевых
при ненулевых ,
то в точке
,
то в точке условный
локальный минимум.
условный
локальный минимум.Если
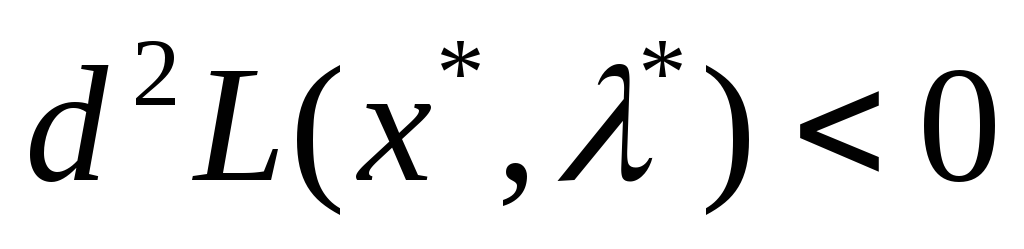 при ненулевых
при ненулевых ,
то в точке
,
то в точке условный
локальный максимум.
условный
локальный максимум.Если
 не
знакопостоянный при ненулевых
не
знакопостоянный при ненулевых ,
то в точке
,
то в точке экстремума нет.
экстремума нет.Если
 знакопостоянный,
но при ненулевых
знакопостоянный,
но при ненулевых обращается в нуль, то требуется
дополнительное исследование.
обращается в нуль, то требуется
дополнительное исследование.
Вычислить значения функции в точках условного экстремума.
Пример. Найти
экстремум функции
![]() при
условии
при
условии![]()
Составим функцию
Лагранжа
![]() .
.
Найдем стационарные
точки
![]() .
.
Решая эту систему
находим
![]() .
.
Исследуем в стационарной точке второй дифференциал функции Лагранжа
![]() .
.
![]() и
и![]() связаны
соотношением
связаны
соотношением![]() .
.
Исследуем
![]() в
стационарной точке
в
стационарной точке![]()
![]() при условии
при условии
![]() .
.
Значит функция
![]() имеет
в точке
имеет
в точке![]() локальный
максимум 2.
локальный
максимум 2.
Нахождение наибольших и наименьших значений функции.
Пусть задана
непрерывно дифференцируемая функция
![]() на
множестве
на
множестве![]() .
.![]() замкнутая
и ограниченная область(компактная).
Тогда
замкнутая
и ограниченная область(компактная).
Тогда![]() достигает
максимума или минимума в некоторых
точках
достигает
максимума или минимума в некоторых
точках![]() .
Эти точки могут быть внутренними и
граничными. Если точка
.
Эти точки могут быть внутренними и
граничными. Если точка![]() внутренняя,
то функция
внутренняя,
то функция![]() имеет
в ней локальный экстремум. Поэтому,
чтобы найти наибольшее(наименьшее)
значение функции, необходимо найти все
стационарные точки, вычислить значения
функции в этих точках и сравнить их со
значениями функции на границе
имеет
в ней локальный экстремум. Поэтому,
чтобы найти наибольшее(наименьшее)
значение функции, необходимо найти все
стационарные точки, вычислить значения
функции в этих точках и сравнить их со
значениями функции на границе![]() .
.
