Операции с облигациями

Облигация – это ценная бумага, которая выпускается эмитентом (государством или корпорацией) на срок T лет (срок погашения), имеет номинальную цену N и приносит инвестору, купившему эту облигацию, определенный доход. Обычно при наступлении срока погашения инвестор получает номинальную цену облигации.

В зависимости от того в какой форме выплачивается инвестору доход облигации делятся на купонные и бескупонные (”с нулевым купоном“ ).

Купонная облигация продается в момент выпуска по номинальной цене N. К купонной облигации прилагаются купоны, по каждому из которых в определенные сроки (k раз в год, k = 1, 2 или 4) эмитент выплачивает инвестору доход в виде процентов от номинальной цены облигации. Этот процент может быть фиксирован на весь срок T или (особенно в условиях инфляции) объявляться на следующий купон после оплаты предыдущего. По окончанию срока T инвестору выплачивается доход по последнему купону и номинальная цена облигации.

Поток платежей по купонной облигации с выплатой купонного дохода два раза в год можно изобразить на оси времени следующим образом:

− N D₁ D₂ D₃ D₄ … D_2T−2 D_2T−1 D_2T+N

0 1 2 … T–1 T t лет

Если процент, указанный на купоне, постоянен и равен r, то купонный доход также постоянен и вычисляется по формуле:

D_i = r N.

Если процент по i-ому купону равен ri, то купонный доход вычисляется по формуле:

D_i = r_i N,

где i = 1, . . . , kT.

За T лет купонная облигация принесет инвестору доход D:

(1)

Пример 1. Купонная облигация с номинальной ценой 100 руб. выпущена сроком на 5 лет с выплатой два раза в год купонного дохода по ставке 5%. Вычислим доход инвестора, купившего одну облигацию.

Решение. По формуле (1) при постоянном проценте r = 0.05, получаем:

D = 2×5×0.05×100 = 50 руб.

Бескупонная облигация продается в момент выпуска со скидкой от номинальной стоимости (с дисконтом), а выкупается в момент окончания срока T по номинальной стоимости. Доход по бескупонной облигации D равен разности между ее номинальной стоимостью и дисконтом:

D = N − C, (2)

где N – номинальная цена облигации, C – величина скидки (дисконт).

Дисконт на бескупонную облигацию тем больше, чем больше срок T, на который выпущена облигация.

Пример 2. Бескупонная облигация, номинальная цена которой равна 100 руб., выпущена сроком на 5 лет с дисконтом, равным 20%. Каков доход инвестора, купившего эту облигацию?

Решение. Скидка с номинальной цены облигации равна:

100×0.2 = 20 руб.,

следовательно, она куплена инвестором за 80 руб. Доход инвестора равен:

100 − 80 = 20 руб.

Облигация в течение всего срока (от момента эмиссии до момента погашения) обращается на рынке ценных бумаг, где имеет рыночную цену, меняющуюся в зависимости от срока, прошедшего с момента эмиссии, и от общей конъюнктуры рынка. Обычно эта цена (рыночная котировка) указывается в процентах от номинальной цены облигации.

Рыночная цена облигации зависит от ее надежности (финансовой стабильности эмитента), от купонной ставки или от дисконта и, конечно, от времени, оставшегося до погашения облигации или до очередной выплаты купонного дохода. С приближением к моменту погашения или к моменту выплаты процентов цена облигации, вообще говоря, растет. Финансовая стабильность эмитента стимулирует повышение рыночной цены облигации. Однако, чем выше финансовая стабильность эмитента, тем, как правило, ниже купонный процент (или дисконт). Самыми надежными считаются облигации, выпущенные государственными учреждениями.

В США за все время существования этого вида ценных бумаг не было ни одного случая неплатежа по ним. Такие случаи возможны в условиях политической нестабильности государства и экономических трудностей.

Для группы бескупонных облигаций одной степени надежности, одинакового уровня ликвидности и других характеристик по статистическим данным можно построить функцию, выражающую зависимость доходности бескупонной облигации от времени, оставшегося до момента погашения. Доходность облигации выражается в процентах, которые составляет доход, полученный от данной облигации, к расходам на ее приобретение, то есть к ее рыночной цене. Эта функция может иметь различный характер.

Облигация с купонным доходом может быть представлена, как несколько бескупонных облигаций, которые принесут те же доходы и в те же сроки, что и купонная облигация. Приведем пример.

Пример 3. Облигация с купонным доходом имеет номинальную цену N и погашается через 4 периода времени, в каждый из которых по купону выплачивается доход, равный D. Определим пакет бескупонных облигаций, которые принесут инвестору тот же доход в те же сроки, что данная бескупонная облигация.

Решение. Изобразим денежный поток, соответствующий данной купонной облигации, на оси времени:

− N D D D N +D

0 1 2 3 4 периоды

Пусть b1, b2, b3 – положительные числа, каждое из которых меньше D, и b1+b2+b3 < N. Составим следующий пакет бескупонных облигаций:

1-я облигация: номинальная цена – D, цена приобретения – b1 (дисконт равен D − b1), срок погашения – первый период;

2-я облигация: номинальная цена – D, цена приобретения – b2 (дисконт равен D − b2), срок погашения – второй период;

3-я облигация: номинальная цена – D, цена приобретения – b3 (дисконт равен D − b3), срок погашения – третий период;

4-я облигация: номинальная цена – (N + D) , цена приобретения – (N − b1 − b2 − b3) (дисконт равен D + b1 + b2 + b3), срок погашения – четвертый период.

Изобразим на осях времени потоки платежей по этим четырем бескупонным облигациям:

1-я облигация: −

− b1 D

0 1 периоды

2-я облигация: −

− b2 D

0 1 2 периоды

3-я облигация: −

− b3 D

0 1 2 3 периоды

4-я облигация: -

b1+b2+b3–N N +D

0 1 2 3 4 периоды

В момент 0 инвестор тратит на покупку этого пакета из четырех бес купонных облигаций сумму N. В моменты 1, 2 и 3 он получает доход, равный D, а в момент 4 он получает сумму N + D.

Таким образом, инвестор получает от составленного пакета бескупонных облигаций тот же доход и в те же сроки, что и от одной купонной облигации.

Будем говорить, что купонная облигация и пакет бескупонных облигаций являются равноценными, если по ним инвестор получает одинаковый доход в одни и те же сроки. Из приведенного примера ясно, что для данной купонной облигации существует бесконечно много равноценных пакетов бескупонных облигаций, так как в качестве цен приобретения облигаций подходят любые положительные числа b1, b2, b3, удовлетворяющие неравенству b1 + b2 + b3 < N.

Арбитражная операция будет невозможна, если доходность купонной облигации и равноценного пакета бескупонных облигаций будут равны. Если в какой-либо момент доходность купонной облигации не равна доходности равноценного пакета бескупонных облигаций, то возникает возможность арбитражной операции.

Из определения доходности следует, что рыночная цена облигации или другой ценной бумаги обратно пропорциональна ее доходности.

Если доходность купонной облигации выше доходности равноценного пакета бескупонных облигаций, то арбитражер покупает купонную облигацию и продает равноценный пакет бескупонных облигаций. При этом арбитражер получает прибыль, так как проданный им пакет бескупонных облигаций имеет большую рыночную цену, чем купонная облигация.

Если доходность купонной облигации, которую имеет инвестор, ниже доходности равноценного пакета бескупонных облигаций, то он продаст купонную облигацию и купит равноценный пакет бескупонных облигаций. При этом он получит арбитражный доход, так как на рынке купонная облигация в этом случае дороже данного пакета.

Введем следующие понятия.

Рыночной (спот) процентной ставкой rt для периода в t лет назовем доходность бескупонной облигации, до погашения которой осталось t лет. Форвардной процентной ставкой называется ставка доходности бескупонной облигации в будущем периоде времени, рассчитанная по ставкам предыдущих периодов. Покажем, как рассчитать форвардную ставку, при которой арбитражная операция с облигациями будет невозможна.

Пример 4. Рыночная ставка r1 на один год равна 10%, рыночная ставка r2 на два года равна 12%. Какова должна быть форвардная ставка r на три года, чтобы арбитражная операция с купонной облигацией, номинальной стоимости 100 руб. и до погашения которой осталось 3 года, была невозможна? Купонный доход равен 6% в год, рыночная цена облигации – 92 руб.

Решение. Арбитражная операция невозможна, если доходность данной купонной облигации и равноценного пакета бескупонных облигаций одинаковы. Это будет выполнено, если современная ценность этого пакета равна цене в настоящий момент купонной облигации, то есть, 92 рублям.

Опишем пакет из трех бескупонных облигаций, равноценный данной купонной облигации. Из условий примера следует, что номинальная цена первой и второй облигаций – 6 рублей, третьей – 106 рублей.

Рыночная ставка r1 на один год равна 10%, поэтому рыночная цена первой бескупонной облигации в момент 0 равна:

руб.

Рыночная ставка r2 на два года равна 12%, поэтому рыночная цена второй бескупонной облигации в момент 0 равна:

руб.

Теперь мы можем определить рыночную цену третьей бескупонной облигации в момент 0:

92 − (5.4545 + 4.7832) = 81.7623 руб.

Изобразим потоки платежей, связанных с этим пакетом бескупонных облигаций, графически (цены облигаций указаны с точностью до копеек):

1-я облигация: −

− 5,45 6

0 1 периоды

2-я облигация: −

− 4,79 6

0 1 2 периоды

3-я облигация: −

− 81,76 106

0 1 2 3 периоды

Очевидно, что этот пакет бескупонных облигаций равноценен данной купонной облигации: за него в момент 0 заплачено 92 руб., в каждый из трех лет получен доход 6% (6 руб.), а в конце третьего года возвращена и номинальная цена облигации – 100 руб. Современная ценность этого пакета в момент 0 будет равна сумме:

Форвардная ставка r является корнем уравнения:

= 92.

Это уравнение равносильно уравнению:

= 92.

Решая это уравнение, находим значение форвардной ставки r на три года:

r = 0.0904 ≈ 9%.

Запишем в общем виде уравнение, определяющее форвардную ставку, исключающую возможность арбитражной операции с данной купонной облигацией и равноценным пакетом бескупонных облигаций.

Пусть до погашения купонной облигации осталось t периодов, в каждый из которых происходит оплата купонов. Номинальная цена облигации – N, купонные платежи равны D1, . . . , Dt. Известны рыночные ставки процента для бескупонных облигаций r1, r2, . . . , rt−1, когда срок до погашения облигации равен 1, 2, . . . , t − 1 год соответственно. Цена купонной облигации в настоящий момент равна P. Современная ценность в момент 0 равноценного этой облигации пакета бескупонных облигаций равна сумме:

.

Значение форвардной процентной ставки r должно определяется из уравнения:

. (3)

Рассмотрим сначала частный случай этого уравнения. Пусть в настоящий момент рыночная ставка процентов для бескупонной облигации на 1 год равна r1, на 2 года – r2. Какова должна быть форвардная ставка r на 1 год в начале второго года, чтобы арбитражная операция была невозможна?

Если инвестор покупает бескупонную облигацию, номинальная стоимость которой равна N и которая выпущена на два года, то в начале двухлетнего периода он должен заплатить за нее сумму:

.

Инвестор может поступить иначе: купить в настоящий момент бескупонную облигацию сроком в 1 год, погасить ее через год и на полученные деньги купить в начале второго года новую облигацию. Какова должна быть форвардная ставка r на один год для новой облигации, чтобы инвестор получил за два года тот же доход, что и раньше, и тем самым была исключена возможность арбитражной операции?

Во втором случае доход инвестора через два года будет равен N, если r удовлетворяет уравнению:

.

Подставив значение N0 в последнее уравнение, получим равенство:

из которого получаем формулу для r:

. (4)

Пример 5. Рыночная ставка процента для бескупонной облигации на один год равна 8%, на два года – 12%. Найдем форвардную ставку r на 1 год в начале второго года, исключающую арбитражную операцию.

Решение. Форвардную ставку r определяем по формуле (4):

или r ≈ 16.5%.

Рассмотрим теперь общую ситуацию. Пусть в момент 0 рыночные ставки процента для бескупонной облигации со сроком выкупа t лет равны rt (t = 1, . . . , n). Выясним, какова должна быть форвардная ставка r для бескупонной облигации, эмитированной в момент n − 1 сроком на 1 год.

Изобразим эту ситуацию на рисунке:

0 1 2 … n–1 n t лет

Форвардная ставка r определяется равенством доходов инвестора за n лет от вложения денег в момент 0 на n лет (нулевая стратегия) и какой-либо другой стратегии.

Нулевая стратегия. Инвестор, чтобы получить в момент n сумму N, вкладывает в момент 0 сумму N0, которая определяется по формуле:

.

Доход инвестора при этом равен N − N0.

Поставим условием, чтобы при любой другой стратегии вложения денег инвестор получил в момент n сумму N, вложив в момент 0 сумму N0. Рассмотрим две возможные стратегии.

Первая стратегия. Инвестор вкладывает в момент 0 сумму N0 сроком на n − 1 год. Тогда в конце n − 1-ого года он получит сумму, равную

.

Полученные деньги он вкладывает в момент n−1 на 1 год под форвардную ставку r. При этом его доход будет равен:

.

Согласно принятому условию, этот доход должен быть равен доходу, полученному при реализации нулевой стратегии, то есть форвардная ставка r определяется из уравнения:

.

Подставив формулу для N0 из нулевой стратегии, получим равенство:

.

откуда получаем формулу для значения r:

. (5)

Вторая стратегия. В момент 0 инвестор вкладывает сумму N0 сроком на t0 лет (t0 < n). В момент t0 он получает сумму

.

Эту сумму он вкладывает на оставшиеся n−t0 лет под форвардную ставку r, которая имеет место в момент t0 для бескупонной облигации, до погашения которой остается n − t0 лет. Изобразим эту ситуацию на оси времени:

0 1 t0 n t лет

Следуя такой стратегии, в момент n инвестор получит сумму, равную

.

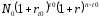Согласно принятому условию, эта сумма должна быть равна N, то есть форвардная ставка r определяется уравнением:

,

откуда получаем формулу для значения r:

. (6)

Заметим, что формула (4) является частным случаем формулы (6) при

t0 = n − 1.

Пример 6. Рыночная ставка процента для бескупонной облигации со сроком выкупа один год равна 10%, два года _ 11%, три года _ 12%, четыре года _ 14%. Найдем форвардную ставку в двух случаях:

а) инвестор вкладывает свои деньги в начале первого года на 3 года и полученную сумму вкладывает в начале четвертого года на 1 год; какова должна быть форвардная ставка в начале четвертого года для бескупонных облигаций со сроком выкупа 1 год?

б) инвестор вкладывает свои деньги в начале первого года на 2 года и полученную сумму вкладывает в начале третьего года на 2 года; какова должна быть форвардная ставка в начале третьего года для бескупонных облигаций со сроком выкупа 2 года?

Решение. а) В этом случае n = 4, r3 = 12%, r4 = 14%. Находим r по формуле (5):

или r = 20.22%.

б) В этом случае n = 4, t0 = 2, r4 = 14%, rt0 = 11%. По формуле (9.11) находим r:

или r = 17.08%.