19. Уравнение Шрёденгера для атома водорода.

Простейшая система, состоящая из электрона е, который движется в кулоновском поле ядра с зарядом Ze, называется водородоподобной. При Z=1 это атом водорода, при Z=2 – однократно ионизированный атом гелия – ион и т.д. Потенциальная энергия взаимодействия электрона с ядром в такой системе равна (1), где r- расстояние между электроном и ядром, которое в первом приближении будем считать точечным.

Уравнение Шредингера в этом случае имеет вид (2)

Поле (1), в котором движется электрон, является центрально-симметричным, т.е. зависит только от r. Поэтому решение уравнения (2) наиболее целесообразно проводит в сферической системе координат , где оператор Лапласа имеет вид

.

20. Физический смысл квантования чисел.

1. Главное квантовое число n. Это квантовое число принимает значения n =1,2,3…, и определяет полную энергию электрона в любом квантовом состоянии Главное квантовое число n характеризует энергию атомной орбитали. Оно может принимать любые положительные целочисленные значения. Чем больше значение n, тем выше энергия и больше размер орбитали.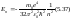

2. Орбитальное квантовое число l - характеризует энергетический подуровень. Атомные орбитали с разными орбитальными квантовыми числами различаются энергией и формой. Для каждого n разрешены целочисленные значения l от 0 до (n−1). Значения l = 0, 1, 2, 3... соответствуют энергетическим подуровням s, p, d, f.

3. Магнитное квантовое число m_l отвечает за ориентацию атомных орбиталей в пространстве. Для каждого значения l магнитное квантовое число ml может принимать целочисленные значения от −l до +l (всего 2l + 1 значений).

Физический смысл магнитного квантового числа вытекает из того, что волновая функция , описывающая квантовое состояние электрона в атоме водорода, является собственной функцией оператора проекции момента импульса , причем .

Поэтому, из общих положений квантовой механики следует, что проекция момента импульса электрона на выделенное в пространстве направление может иметь только определенные значения, равные.

4. Электрон, занимающий определенную орбиталь, характеризуется тремя квантовыми числами, описывающими эту орбиталь и четвертым квантовым числом (спиновым) m_s, которое характеризует спин электрона - одно из свойств (наряду с массой и зарядом) этой элементарной частицы. Спин - собственный магнитный момент количества движения элементарной частицы. Хотя это слово по-английски означает "вращение", спин не связан с каким-либо перемещением частицы, а имеет квантовую природу. Спин электрона характеризуется спиновым квантовым числом ms, которое может быть равно +1/2 и −1/2.

Квантовые числа, возникающие при решении волнового уравнения, служат для описания состояний квантово-химической системы. Каждая атомная орбиталь характеризуется набором из четырех квантовых чисел: главного n, орбитального l, магнитного m_l и спинового m_s.

Энергетический спектр (закон дисперсии) — зависимость энергии частицы от импульса. Для свободной частицы закон дисперсии изотропен и зависит квадратично от импульса. Такой же параболический закон дисперсии встречается в физике твёрдого тела, поскольку при движении электрона в кристаллах, таких как кремний или арсенид галлия в низкоэнергетическом пределе закон дисперсии имеет параболическую зависимость от квазиимпульса вблизи дна зоны проводимости. В твёрдом теле по аналогии со свободной частицей вводят эффективную массу для частиц, отличную от массы частицы в вакууме и в общем слуае имеет место зависимость этой массы от направления в кристалле. Энергетический спектр частиц в твёрдом теле имеет более сложную структуру по сравнению со свободной частицей. Его знание очень важно для предсказания транспортных, оптических свойств электронного и дырочного газа в полупроводниках.

Правила отбора устанавливают допустимые квантовые переходы между уровнями энергии квантовой системы (атома, молекулы, кристалла, атомного ядра, элементарной частицы) при наложении на неё внеш. возмущений. Если состояния системы характеризуются с помощью квантовых чисел, то О. п. определяют их возможные изменения при квантовых переходах рассматриваемого типа.

Различают строгие и приближённые ПО. Квантовый переход наз. запрещённым, если нарушается хотя бы одно ПО. Строгие ПО обусловлены симметрией системы и строгими законами сохранения и налагают абс. запреты на квантовые переходы. Приближённые О. п. характеризуют переходы между уровнями энергии, к-рые описываются приближёнными законами сохранения. Квантовое число полного угл. момента атома (J)или молекулы (F)является точным, т. к. полный угл. момент является инвариантом группы вращения, поэтому ПО для J (или F) - строгие. В случае электрич. дипольных переходов возможны изменения квантовых чисел:J = J - J'= 0, 1 вМ = М - М' = 0,1 (где J, J' - квантовые числа полного момента атома в начальном и конечном состояниях, М, М' - квантовые числа проекций полных моментов на к--л. ось). Для электрич. квадрупольных переходовJ = 0, 1,2 (J + J'2),М = 0,1,2.  В случае, когда не учитываются слабые взаимодействия, О. п. по чётности состояний (+ - для электрич. дипольных переходов, + + и - - для электрич. квадрупольных переходов и т. д.) также являются строгими. О. п. нарушаются в сильных внеш. полях за счёт поляризуемости атома или молекулы или при многофотонном поглощении.

21. СПИН. Помимо энергии, связанной с движением вокруг ядра атома, электрон обладает еще и дополнительной энергией, связанной с вращением вокруг своей оси наподобие волчка, откуда и происходит слово спин (спин — по-английски верчение). Поскольку же электрон имеет электрический заряд, то при его вращении возникает круговой электрический ток, а следовательно, и магнитное поле, превращающее электрон в маленький электромагнитик, имеющий два магнитных полюса. Так как электрон может вращаться в разных направлениях — по часовой стрелке и против нее, то он может пребывать в двух различных энергетических, или, как говорят, спиновых, состояниях. Спин электрона вызывает ряд дополнительных взаимодействий, играющих исключительно важную роль в физических свойствах атома. Спином обладают и другие элементарные частицы: протон, нейтрон, а также кванты излучений — фотоны. Согласно законам квантовой теории спин имеет строго определенную величину, характерную для данной частицы. В системе единиц, принятой в квантовой теории, спин электрона, а также протона и нейтрона равен 1/2. Спин фотона равен 1.

Водородоподобный атом – система, состоящая из положительно заряженного ядра, и локализованного вблизи него одного электрона. Эти атомы, как и любые другие, имеют линейчатые спектры излучения и поглощения.

ТОНКАЯ СТРУКТУРА (мультиплетное расщепление) уровней энергии - расщепление уровней энергии (термов) атома, молекулы или кристалла, обусловленное гл. обр. спин-орбитальным взаимодействием. Тонкое расщепление уровней - причина возникновения T. с. спектральных линий. Мультиплетное расщепление электронных уровней энергии молекул связано с т. н. взаимодействием спин - ось.

22. Спектры щелочных металлов. Спектры испускания атомов щелочных металлов, как и спектр атома водорода, состоят из множества спектральных линий. Кропотливая систематика этих спектральных линий позволила сгруппировать их в серии, каждая из которых связана с переходом возбужденного атома на какой-то определенный уровень. В некотором смысле атомы щелочных металлов являются водородоподобными, однако не полностью. Дело в том, что внешний электрон несколько деформирует электронный остов и тем самым искажает поле, в котором движется.