Стереометрия

С6 Объем прямоугольного параллелепипеда равен 162 дм². Найти площадь полной поверхности параллелепипеда, если стороны основания и высота относятся как 1:2:3.

С6 Дана правильная четырехугольная призма, площадь полной поверхности которой равна 1296 дм², а диагональ её равна 27 дм. Найти сторону основания и боковое ребро

С6 Дана треугольная пирамида, стороны основания которой равны 1,5м, 1,4м и 1,3 м. Боковое ребро, противолежащее стороне длиной 1,4м, перпендикулярно плоскости основания и равно 1,6м. Найти площадь полной поверхности пирамиды.

С6 Требуется покрасить 150 урн, имеющих форму цилиндра без крышки. Радиус основания равен 15 см., высота равна 60 см. Сколько будет израсходовано краски, если на 1 м² расходуется 200г?

С6 Объем цилиндра равен 1,92 м², а площадь боковой поверхности равна 0,48π м². Найти диагональ осевого сечения цилиндра.

С6 Образующая конуса равна 40 см и наклонена к плоскости основания под углом 60°. Найти площадь боковой поверхности конуса.

С6 Радиусы оснований усеченного конуса равны 20 и 8 см. Найти площадь боковой поверхности конуса, если его высота равна 16 см.

С6 Найти площадь полной поверхности усеченного конуса, если его объем равен 6520 дм², а образующая и радиусы оснований относятся как 17:11:3.

С6 Найти площадь поверхности шара, если его объем равен 36 см³.

С6 Около шара описан цилиндр. Найти отношение их объемов.

С6 В окружность основания цилиндра вписан правильный треугольник. С6 Найдите объем пирамиды той же высоты, что и цилиндр, в основании которого лежит этот треугольник, если объем цилиндра равен

С6 Найти объём шара, если его диаметр равен 4 .

С6 Найти площадь поверхности шара, если его равен 2.

С6 Найти площадь поверхности шара, если его равен 4.

С6 Найти объём гексаэдра, если его длина ребра равна 2.

С6 Найти объём гексаэдра, если его длина ребра равна 3.

С6 Найти площадь поверхности гексаэдра, если его длина ребра равна 2

С6 Найти площадь поверхности гексаэдра, если его длина ребра равна 3

С6 Площадь основания прямого параллелепипеда равна 12. Найти его объём, если высота равна 4.

С6 Дана правильная четырёхугольная пирамида. Длина ребра в основании равна 2. Найти объём этой пирамиды, если её высота равна 3.

C6 Объем конуса равен 12. Параллельно основанию проведено сечение, делящее высоту конуса пополам. Найдите объем отсеченного конуса.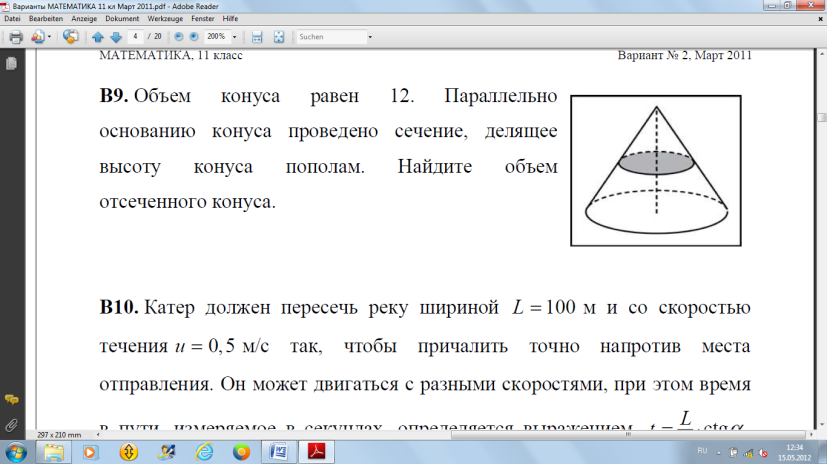

C6 Гранью параллелепипеда является ромб со стороной 3 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.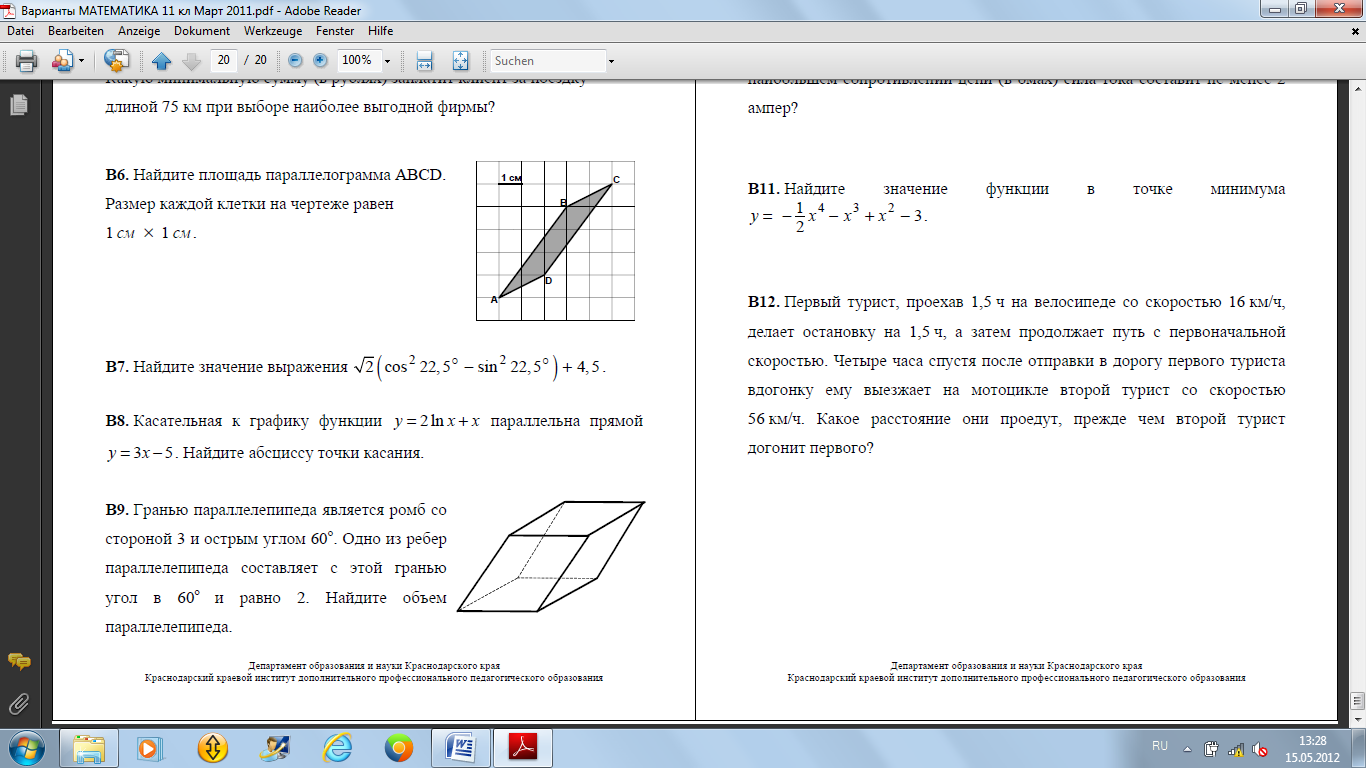

C6 Высота прямой четырехугольной призмы равна 11см, а стороны основания 4см, 3см. Найти площадь осевого сечения

C6 Измерения прямоугольного параллелепипеда 15м, 50м и 36м. Найти ребро равновеликого ему куба

С5 Вычислить интеграл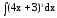

C6 Площадь основания тетраэдра равна 9 см², а высота – 5см. Найти объем тетраэдра.

C6 Высота боковой грани правильной треугольной пирамиды равна 3см, сторона основания равна 2см. Вычислить боковую поверхность пирамиды

C6 Высота боковой грани правильной четырехугольной пирамиды равна 4см, сторона основания равна 1,5см. Вычислить боковую поверхность пирамиды

C6 Запишите координаты центра сферы, если уравнение сферы имеет вид

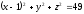
C6 Запишите координаты центра сферы и ее радиус, если уравнение сферы имеет вид

C6 Из точки к плоскости проведены две наклонные, равные 23 см и 33 см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3.

C6 Из точки к плоскости проведены две наклонные, одна из которых на 26 см больше другой. Проекции наклонных равны 12 см и 40 см. Найдите наклонные.

C6 Из точки, лежащей вне плоскости проведены две наклонные, сумма длин которых равна 12 дм. Проекции этих наклонных 1 дм и 7 дм. Найти длину каждой наклонной.

C6 Прямые AB, AC, AD попарно перпендикулярны. Найдите отрезок CD, если BD=9 см, ВС=16 см, AD=5 см

C6 Из точки к плоскости проведены две наклонные, которые относятся как 1:2. Найти длины наклонных, если их проекции равны 1см и 7 см.

C6 Высота пирамиды разделена на 4 равные части и через точки деления плоскости проведены плоскости параллельные основанию. Площадь основания равна 400см². Найти площадь каждого сечения?

C6 Высота цилиндра 6см, радиус основания5см. Найти площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4м от нее.

C6 Шар пересечен плоскостью на расстоянии 6см от центра, радиус сечения 8см. Найти радиус шара?

C6 Из точки к плоскости проведены две наклонные, равные 10 см и 17 см. Разность проекций этих наклонных равна 9 см. Найти проекции наклонных.

C6 Прямые AB, AC, AD попарно перпендикулярны. Найти отрезок CD, если AB=3см, BC=7см, AD=1,5см

C6 Боковая поверхность правильной четырехугольной призмы равна 32 м², а полная поверхность 40м². Найдите высоту.

C6 Боковое ребро прямого параллелепипеда равно 5м, стороны основания равны 6м и 8м. Найти диагонали параллелепипеда.

C6 Измерения прямоугольного параллелепипеда 15м, 50м и 36м. Найти ребро равновеликого ему куба.

C6 Кирпич размером 25×12×6,5 см имеет массу 3,51 кг. Найти его плотность (г/см³).

C6 Измерения прямоугольного бруска 3см, 4см и 5 см. Если увеличить каждое ребро на х сантиметров, то поверхность увеличится на 54 см². Во сколько раз увеличится его объем?

C6 Основание пирамиды – прямоугольник со сторонами 9м и 12м; все боковые ребра равны 12,5м. Найдите объем пирамиды.

C6 Полуцилиндрический свод подвала имеет 6м длины и 5,8м в диаметре. Найдите полную поверхность подвала (без пола).

C6 Конусообразная палатка высотой 3,5м с диаметром основания 4м покрыта парусиной.. Сколько квадратных метров парусины пошло на палатку (без дна)?

C6 Крыша силосной башни имеет форму конуса. Высота крыши 2м, диаметр башни 6м. Найдите поверхность крыши.

C6 Сколько квадратных метров латунного листа потребуется, чтобы сделать рупор, у которого диаметр одного конца 0,43м, другого конца 0,036м и образующая 1,42м?