
- •Вещественные и комплексные числа
- •1.1. Множества. Обозначения. Логические символы
- •1.2. Вещественные числа и их основные свойства
- •Основные свойства вещественных чисел
- •1.3. Абсолютная величина числа
- •1.4. Геометрическое изображение вещественных чисел
- •1.5. Наиболее употребляемые числовые множества
- •1.6. Прямоугольная система координат на плоскости Две взаимно перпендикулярные оси Ох иОу, имеющие общее началоОи одинаковую масштабную единицу, образуютпрямоугольную систему координат на плоскости.
- •1.7. Полярная система координат
- •1.8. Комплексные числа. Алгебраическая форма комплексного
- •1.9. Тригонометрическая форма комплексного числа
- •1.10. Возведение комплексного числа в степень с целым показателем. Формула Муавра
- •1.11. Извлечение корня из комплексного числа
- •1.12. Извлечение квадратного корня из комплексного числа
- •1.13. Показательная форма комплексного числа
- •Многочлены
- •Над многочленами. Корни многочленов. Теорема Безу
- •2.2. Схема Горнера
- •2.3. Кратные корни
- •2.4. Наибольший общий делитель двух многочленов. Алгоритм Евклида
- •Свойства делимости многочленов
- •2.5. Взаимно простые многочлены
- •Свойства взаимно простых многочленов
- •2.6. Корни квадратного уравнения
- •2.7. Корни кубического уравнения
- •2.8. Корни уравнения четвертой степени
- •Индивидуальные задания по теме
2.6. Корни квадратного уравнения
Пусть дано квадратное
уравнение
![]() с любыми коэффициентами. Это уравнение
можно переписать в виде
с любыми коэффициентами. Это уравнение
можно переписать в виде![]() ,
следовательно,
,
следовательно,![]() ,
или
,
или![]() .
Выражение
.
Выражение![]() рассматривается как комплексное число,
поэтому квадратный корень из этого
выражения принимает два значения.
рассматривается как комплексное число,
поэтому квадратный корень из этого
выражения принимает два значения.
П р и м е р.Решить уравнение![]() .
.
Решение.Согласно полученной ранее формуле![]()
![]() .
Найдем
.
Найдем![]() .
Пусть
.
Пусть![]() .
Тогда
.
Тогда![]() .
Из равенства комплексных чисел следует,
что
.
Из равенства комплексных чисел следует,
что![]() ,
,![]() .
Из второго уравнения
.
Из второго уравнения![]() ,
поэтому
,
поэтому![]() ,
или
,
или![]() .
Решив последнее уравнение, находим
.
Решив последнее уравнение, находим![]() ,
т. е.
,
т. е.![]() ,
или
,
или .
По правилу извлечения квадратного корня
из комплексного числа
.
По правилу извлечения квадратного корня
из комплексного числа![]() ,
т. е.
,
т. е.![]() ,
или
,
или![]() ,
,![]() .
.
2.7. Корни кубического уравнения
Пусть дано кубическое
уравнение
![]() .
Введем новую переменную
.
Введем новую переменную![]() .
Тогда исходное уравнение преобразуется
следующим образом:
.
Тогда исходное уравнение преобразуется
следующим образом:![]() или
или
![]() ,
(2.3) где
,
(2.3) где
![]() ,
,![]() .
.
Корни уравнения (2.3) вычисляются по формулам Кардана:
![]()
![]() .
.
Пусть один из
![]() равен
равен![]() ,
а один из
,
а один из![]() равен
равен![]() ,
причем
,
причем![]() ,
тогда
,
тогда![]() .
Однако уравнение третьей степени имеет
три корня:
.
Однако уравнение третьей степени имеет
три корня:![]() ,
,![]() и
и![]() .
Корни
.
Корни![]() ,
,![]() ,
,![]() расположены на окружности радиусом
расположены на окружности радиусом![]() ,
причем
,
причем![]() ,
,![]() ,
т. е.
,
т. е.![]() и
и![]() .
Аналогично находим, что
.
Аналогично находим, что![]() и
и![]() .
Пары
.
Пары
![]() ,
,![]() (
(![]() ,
,
![]() )
выбираются таким образом, чтобы
)
выбираются таким образом, чтобы![]() .
Этому условию удовлетворяют пары (
.
Этому условию удовлетворяют пары (![]() )
и (
)
и (![]() ).
Корни уравнения (2.3) задаются соотношениями:
).
Корни уравнения (2.3) задаются соотношениями:![]() ,
,![]() ,
,![]() .
Корни исходного уравнения
.
Корни исходного уравнения![]() ,
,![]()
П р и м е р.Решить уравнение![]() .
.
Решение.В
данном уравнении![]() ,
,![]() ,
,![]() ,
поэтому
,
поэтому![]() или
или![]() .
Подставляя
.
Подставляя![]() в исходное уравнение, получим
в исходное уравнение, получим![]() ,
в котором
,
в котором![]() ,
,![]() .
Поэтому
.
Поэтому![]() ,
,![]() ,
,![]() ,
,![]() .
Таким образом,
.
Таким образом,![]() ,
,![]() .
Учитывая, что
.
Учитывая, что![]() ,
находим решения исходного уравнения:
,
находим решения исходного уравнения:![]() ,
,![]() .
.
2.8. Корни уравнения четвертой степени
Уравнение четвертой степени
![]() (2.4)
решается методом Феррари. Преобразуем
левую часть (2.4) с помощью вспомогательного
параметра
(2.4)
решается методом Феррари. Преобразуем
левую часть (2.4) с помощью вспомогательного
параметра
![]() следующим образом:
следующим образом:
![]()
![]() .
(2.5) Параметр
.
(2.5) Параметр
![]() подбирается таким образом, чтобы
выражение, стоящее во вторых скобках
правой части, было квадратом двучлена
первой степени.
подбирается таким образом, чтобы
выражение, стоящее во вторых скобках
правой части, было квадратом двучлена
первой степени.
Следовательно,
должно выполняться условие
![]() .
.
Это уравнение
третьей степени относительно
![]() ,
которое решается по формулам Кардана.
Пусть
,
которое решается по формулам Кардана.
Пусть![]() − один из корней этого уравнения. Тогда
выражение
− один из корней этого уравнения. Тогда
выражение![]() приводится к виду:
приводится к виду:
 ,
,
где
![]() ,
, ,
а уравнение (2.4) принимает вид
,
а уравнение (2.4) принимает вид
![]() или
или
![]() .
.
Решение последнего уравнения сводится к решению двух квадратных уравнений.
П р и м е р.
Решить уравнение![]() .
.
Решение.Введем
дополнительный параметр![]() и преобразуем левую часть исходного
уравнения:
и преобразуем левую часть исходного
уравнения:
![]()
![]() .
.
Рассмотрим уравнение
![]() .
Это уравнение имеет один кратный корень,
если
.
Это уравнение имеет один кратный корень,
если![]() ,
т. е. выполняется равенство
,
т. е. выполняется равенство
![]() .
.
При решении этого
уравнения получаем, что один из его
корней
![]() .
При этом значении
.
При этом значении![]() уравнение принимает вид
уравнение принимает вид
![]() ,
т. е.
,
т. е.
![]() .
.
Из полученных
соотношений находим корни исходного
уравнения:
![]() ,
,![]() .
.
Индивидуальные задания по теме
«Комплексные числа»
ВАРИАНТ 1
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
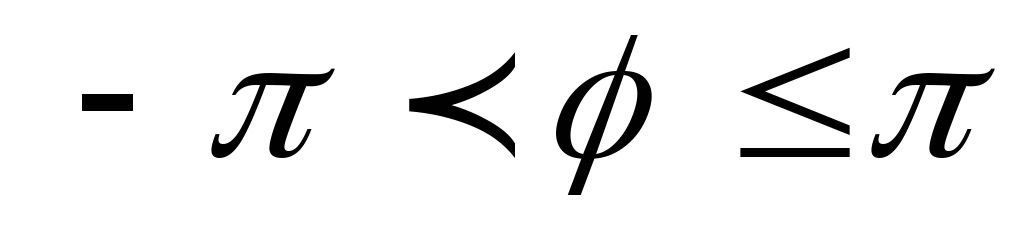 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих неравенству
 .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество:
 .
.
ВАРИАНТ 2
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
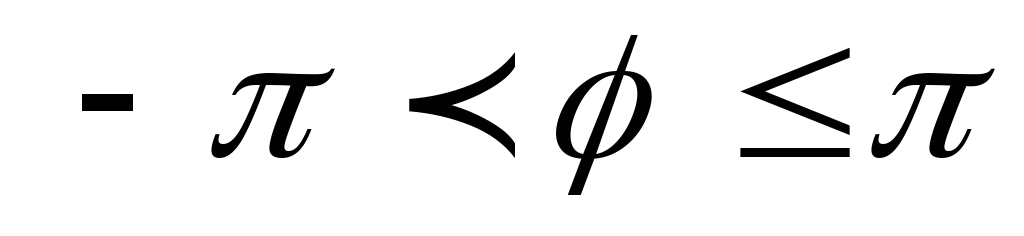 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 ,
, .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
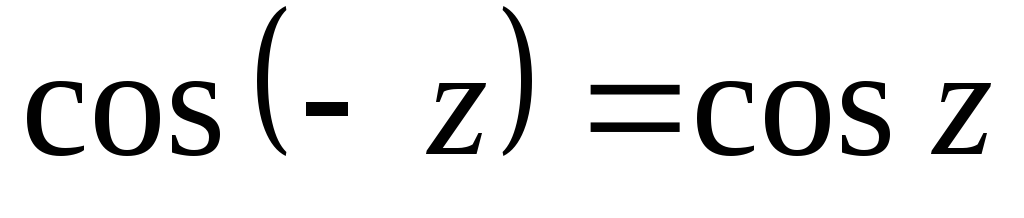 .
.
ВАРИАНТ 3
Найти действительную и мнимую части комплексного числа
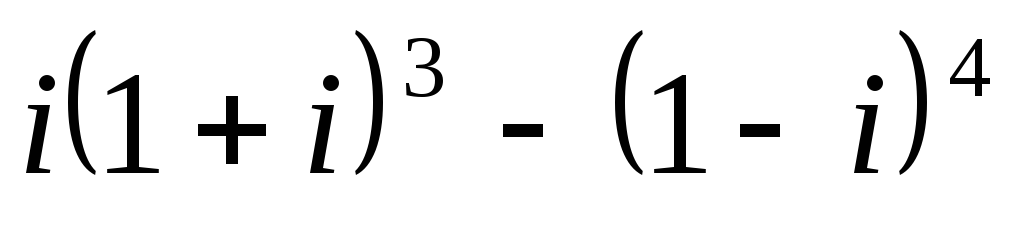 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 .
.
ВАРИАНТ 4
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 .
.
ВАРИАНТ 5
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 ,
, .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 .
.
ВАРИАНТ 6
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
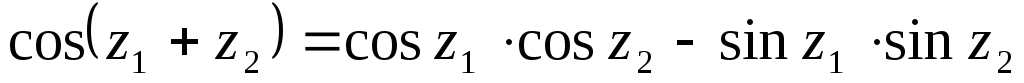 .
.
ВАРИАНТ 7
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа
Найти все значения корней и построить их на комплексной плоскости
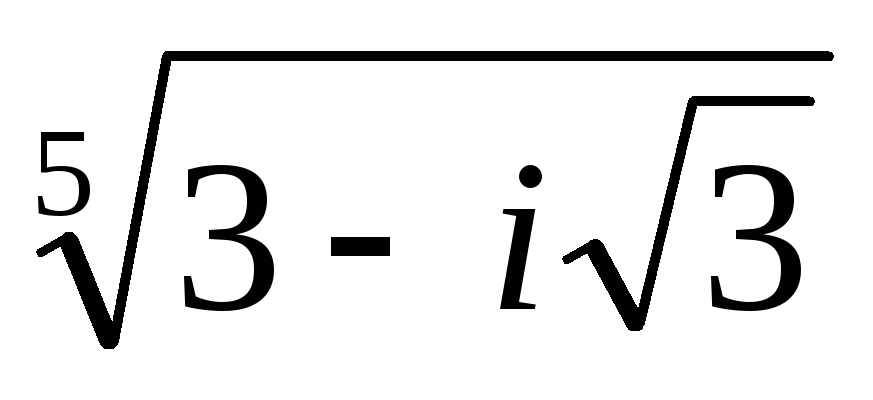 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 .
.
ВАРИАНТ 8
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
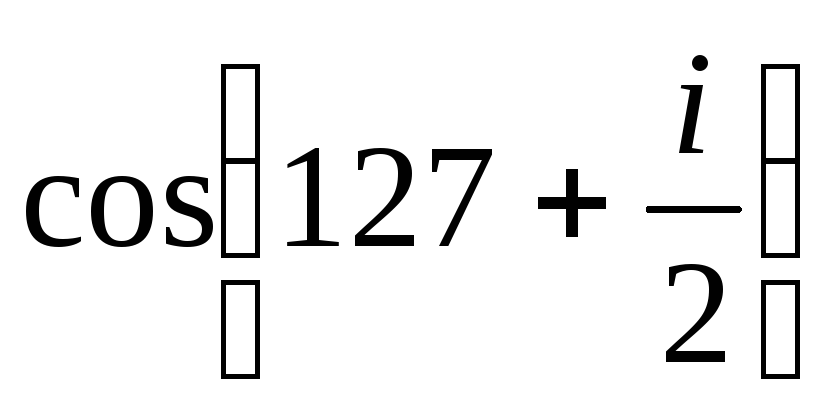 .
.Доказать тождество
 .
.
ВАРИАНТ 9
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа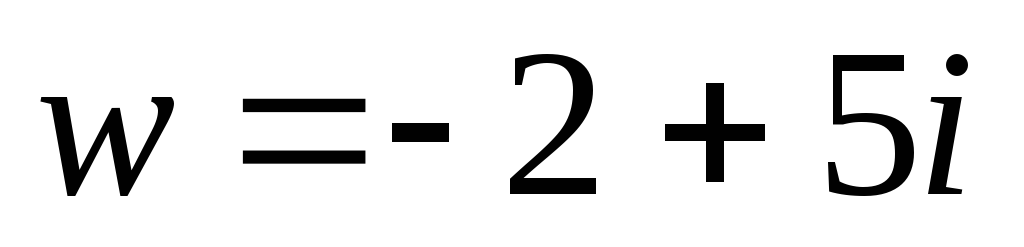 .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 .
.
ВАРИАНТ 10
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 ,
, .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 .
.
ВАРИАНТ 11
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 ,
, .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 ,
, .
.
ВАРИАНТ 12
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 ,
, .
.
ВАРИАНТ 13
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
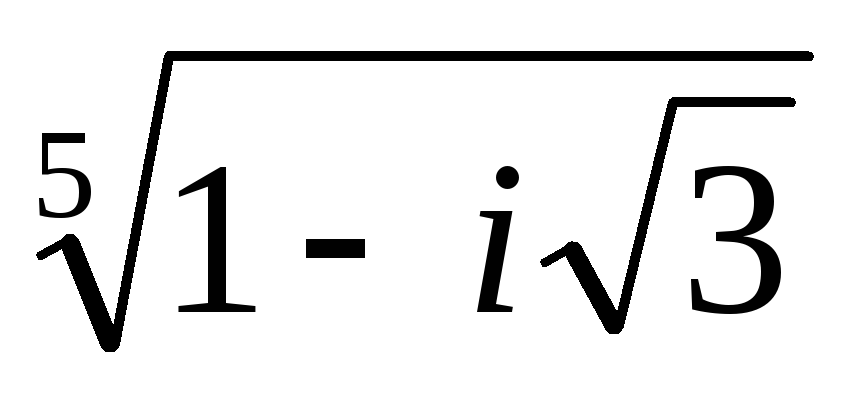 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 ,
, .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 .
.
ВАРИАНТ 14
Найти действительную и мнимую части комплексного числа
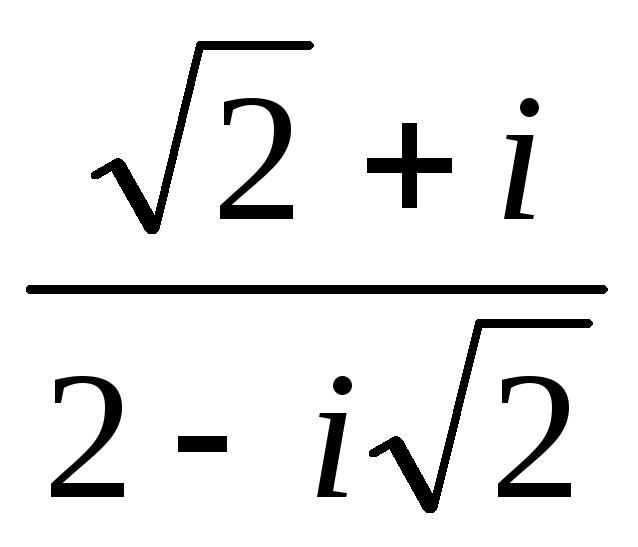 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
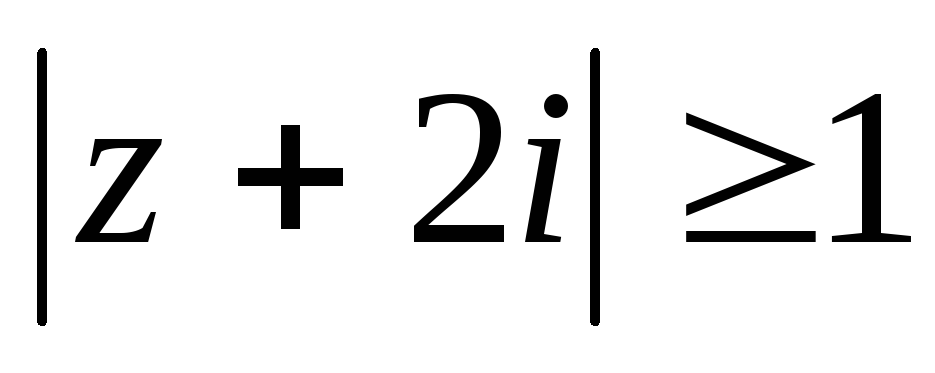 ,
, .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 ,
,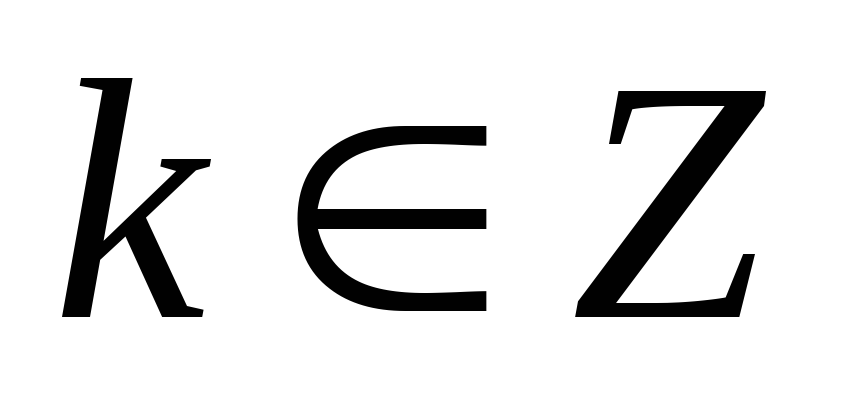 .
.
ВАРИАНТ 15
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 ,
, .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 ,
, .
.
ВАРИАНТ 16
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
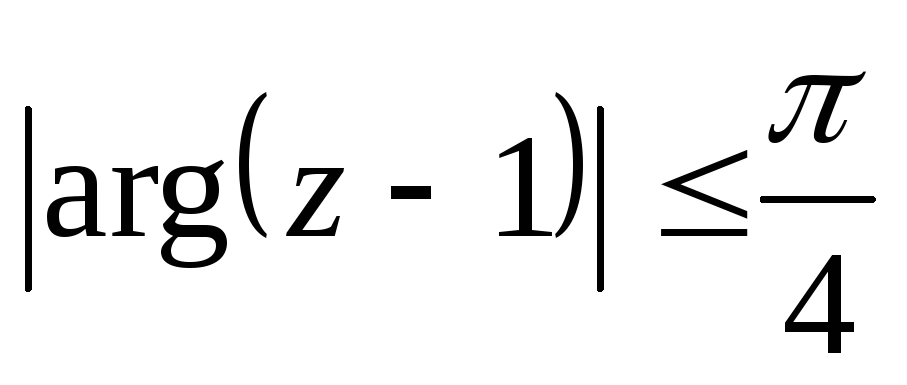 ,
, .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
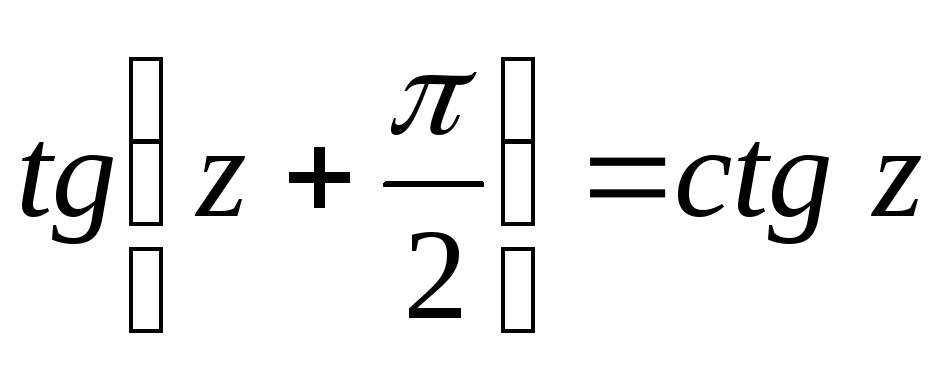 .
.
ВАРИАНТ 17
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 ,
, .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 .
.
ВАРИАНТ 18
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 ,
,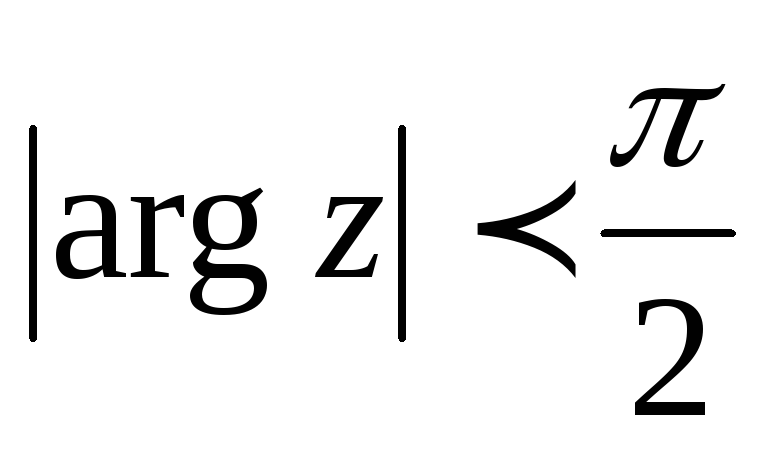 .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])

Доказать тождество
 .
.
ВАРИАНТ 19
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 ,
,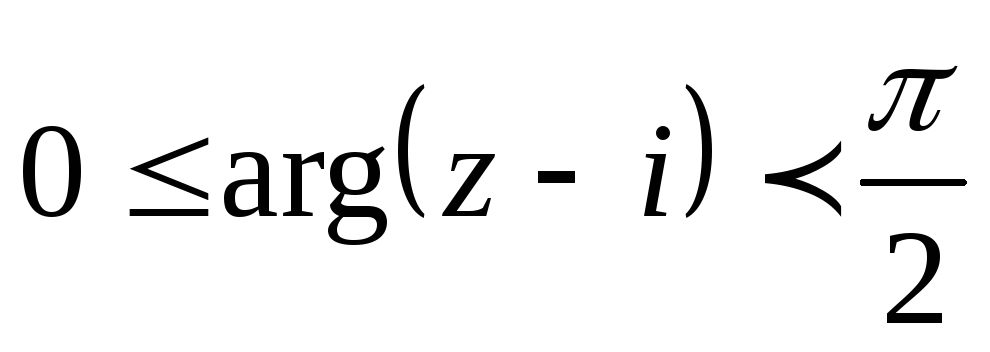 .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 .
.
ВАРИАНТ 20
Найти действительную и мнимую части комплексного числа
 .
.Найти модуль и главное значение аргумента (
 )
комплексного числа
)
комплексного числа .
.Найти все значения корней и построить их на комплексной плоскости
 .
.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным неравенствам
 ,
, .
.Представить в алгебраической форме значение функции комплексного переменного (главное значение аргумента находится в промежутке ; ])
 .
.Доказать тождество
 .
.
Индивидуальные задания по теме «Многочлены»
ВАРИАНТ 1
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня 1 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов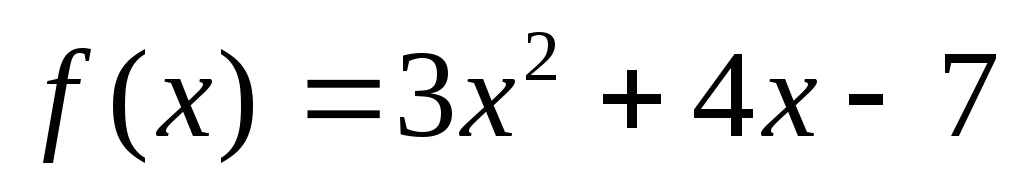 и
и .
.Найти корни уравнения
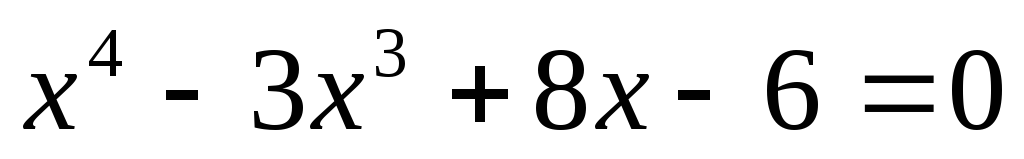 .
.
ВАРИАНТ 2
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня 2 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 3
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня 1 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 3
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня 3 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 5
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня -1 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и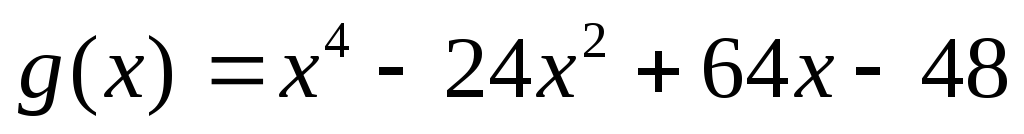 .
.Найти корни уравнения
 .
.
ВАРИАНТ 6
Найти остаток от деления многочлена
 на многочлен
на многочлен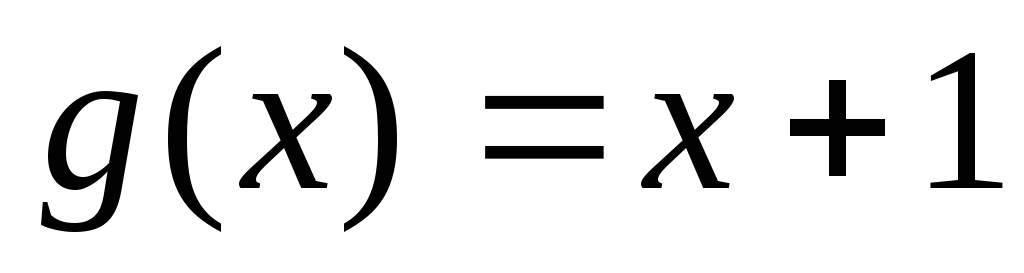 .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня 2 для многочлена
 ?
?Найти наибольший общий делитель
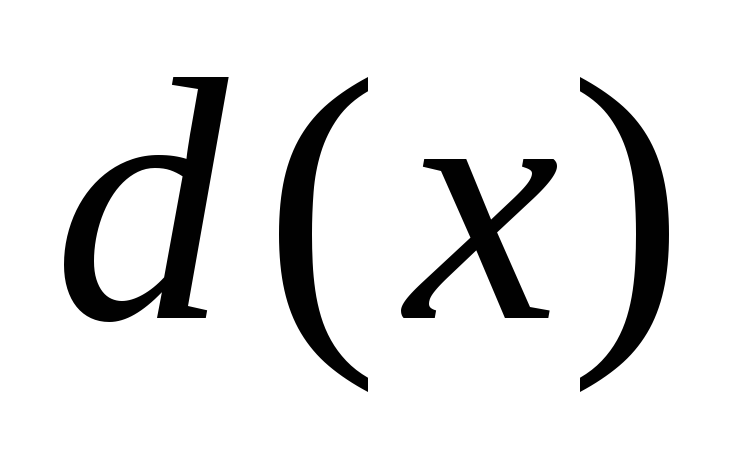 многочленов
многочленов и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 7
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня 1 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и .
.Найти корни уравнения
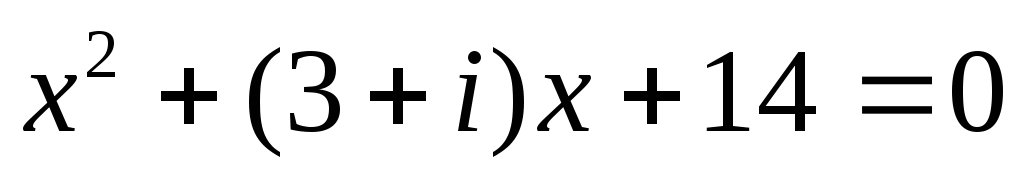 .
.
ВАРИАНТ 8
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня 1 для многочлена
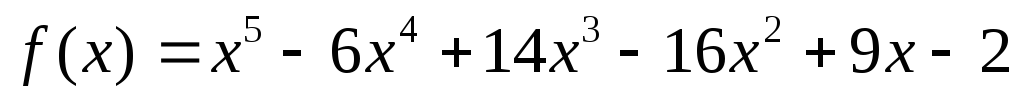 ?
?Найти наибольший общий делитель
 многочленов
многочленов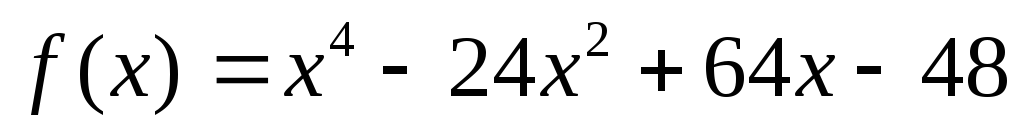 и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 9
Найти остаток от деления многочлена
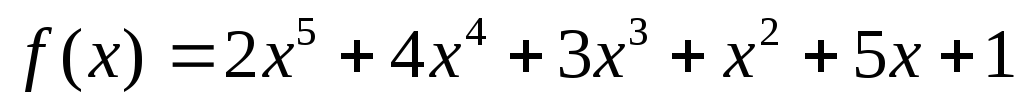 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
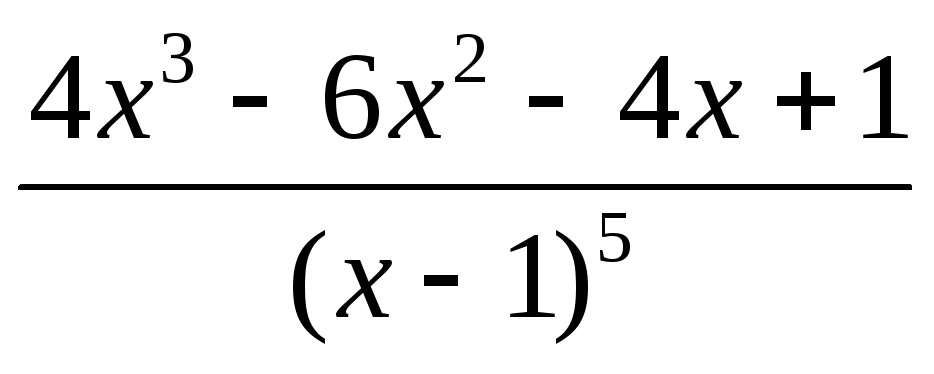 .
.Чему равен показатель кратности корня -1 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 10
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
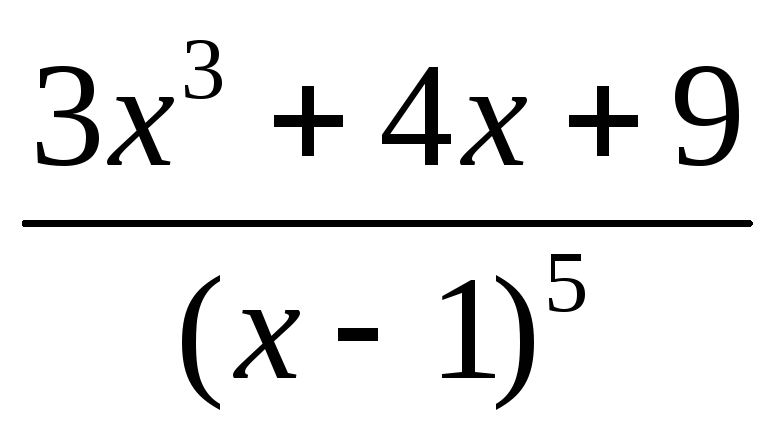 .
.Чему равен показатель кратности корня 1 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 11
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня 2 для многочлена
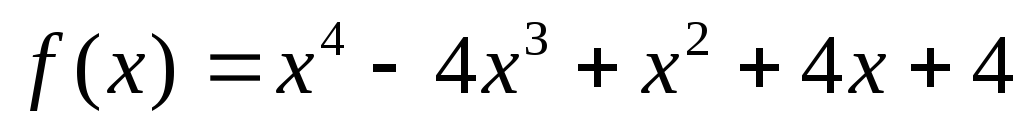 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 12
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня -1 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 13
Найти остаток от деления многочлена
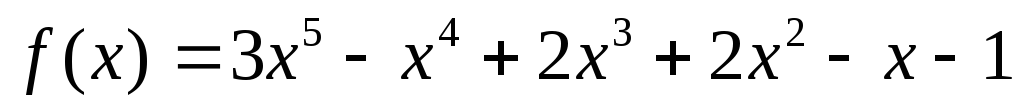 на многочлен
на многочлен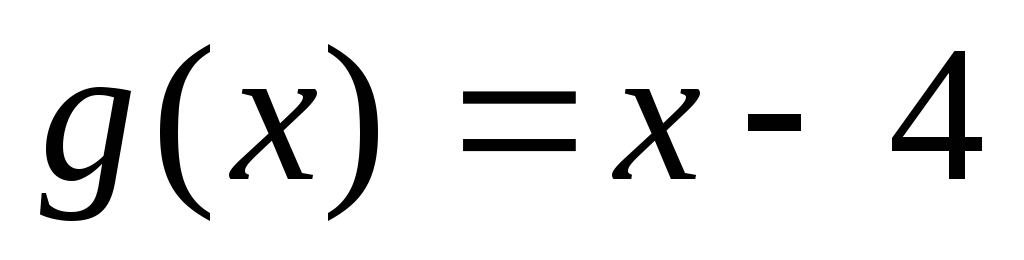 .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня 3 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и .
.Найти корни уравнения
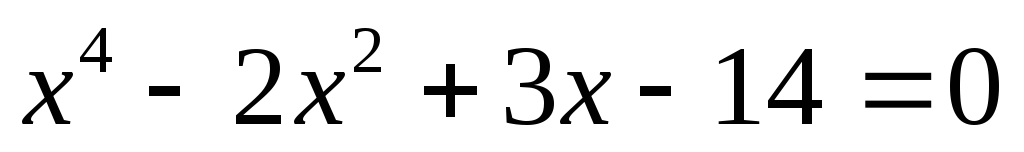 .
.
ВАРИАНТ 14
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня -1 для многочлена
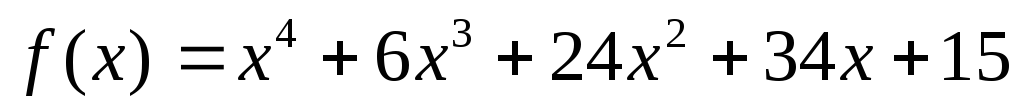 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и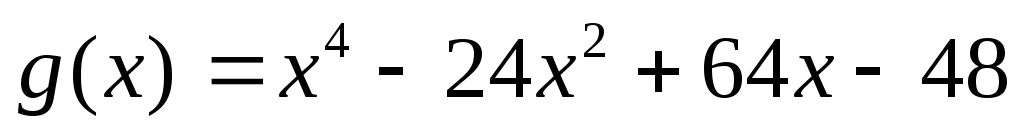 .
.Найти корни уравнения
 .
.
ВАРИАНТ 15
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
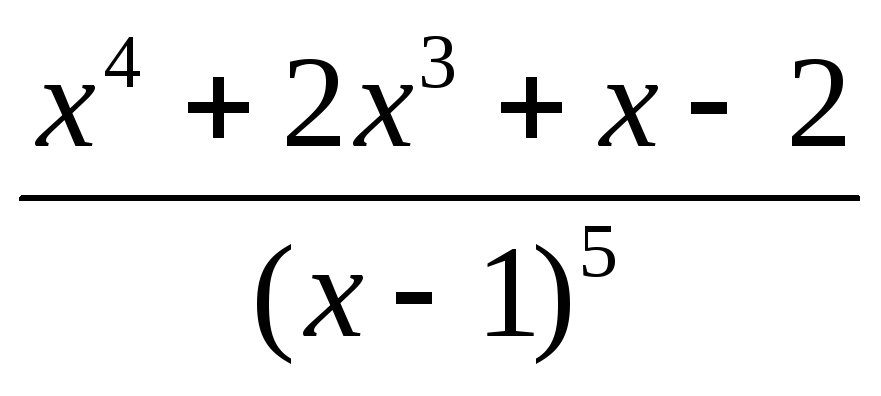 .
.Чему равен показатель кратности корня 2 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов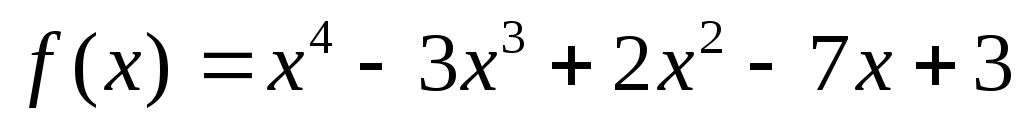 и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 16
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня -1 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 17
Найти остаток от деления многочлена
 на многочлен
на многочлен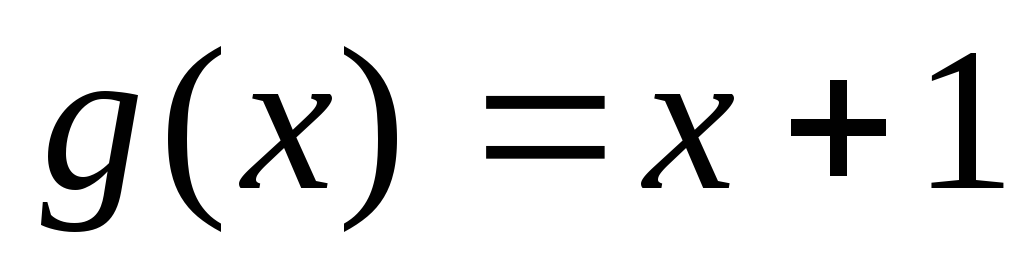 .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня 1 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и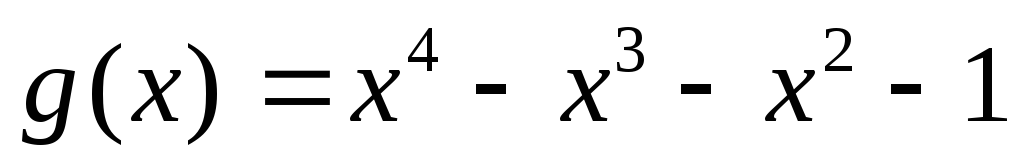 .
.Найти корни уравнения
 .
.
ВАРИАНТ 18
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня -1 для многочлена
 ?
?Найти наибольший общий делитель
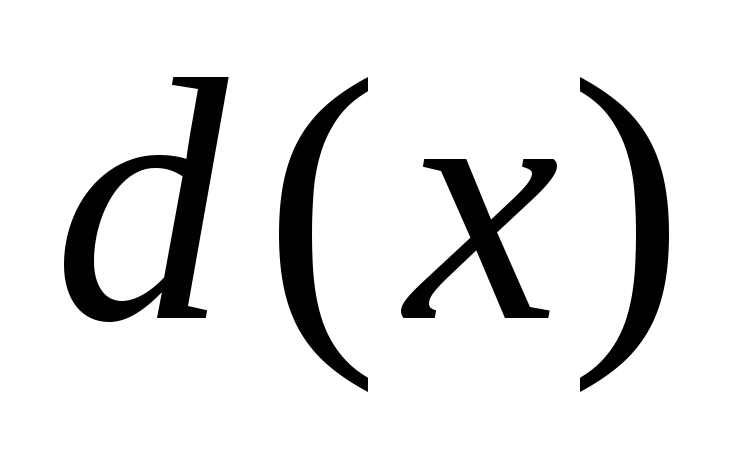 многочленов
многочленов и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 19
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня 1 для многочлена
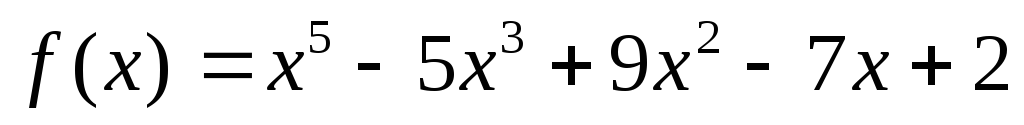 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и .
.Найти корни уравнения
 .
.
ВАРИАНТ 20
Найти остаток от деления многочлена
 на многочлен
на многочлен .
.Пользуясь схемой Горнера, разложить на простейшие дроби выражение
 .
.Чему равен показатель кратности корня 2 для многочлена
 ?
?Найти наибольший общий делитель
 многочленов
многочленов и
и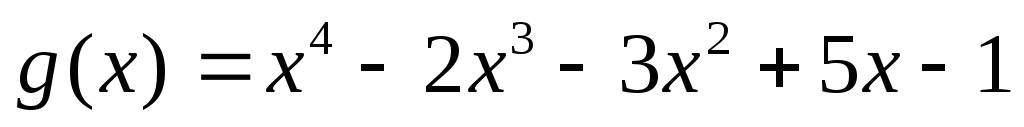 .
.Найти корни уравнения
 .
.
