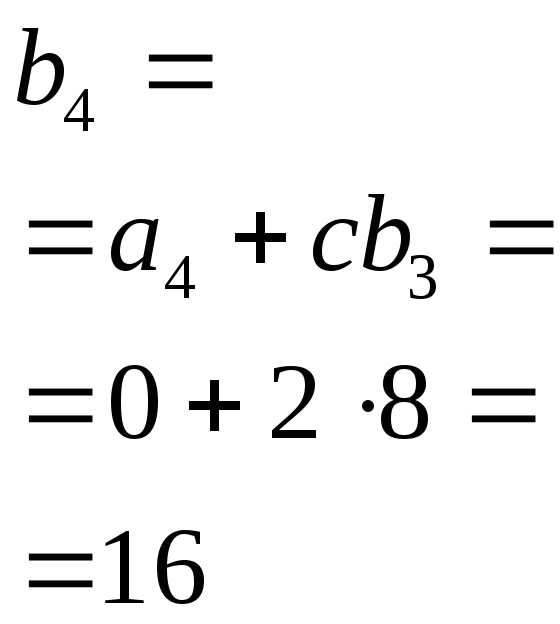2.2. Схема Горнера

Теорема.Пустьи. Найдутся многочлени числотакие, что.

Доказательство. Будем искатьв виде. Из равенства=при сравнении коэффициентов получаем цепочку равенств:,,, . . . ,,, откуда последовательно определяются коэффициентыи остаток:

, ,

,…, ,

.

Теорема доказана. Более того, получен очень удобный способ вычисления коэффициентов и остатка. Этот способ носит названиесхемы Горнера.

П р и м е р.Найти неполное частное и остаток от деления многочленана линейный двучлен.

Решение.Составим таблицу:

Таким образом, неполное частное , остаток 32.

П р и м е р.Пользуясь схемой Горнера, разложить на простейшие дроби выражение.

Решение.Разложим числительпо степенямс использованием схемы Горнера:

	1	0		-1		1
2	1	2		3		7
2	1	4		11
2	1	6
2	1

Таким образом, . Следовательно,.

2.3. Кратные корни

Определение.Если, где многочленуже не делится на, то числокназываетсякратностью корнясв многочлене, а сам кореньс–к-кратным корнемэтого многочлена. Еслик= 1, то говорят, что кореньспростой.

Теорема.Если числосявляетсяк-кратным корнем многочлена, то прионо будет (к−1)-кратным корнем первой производной этого многочлена. Если же, тосне будет служить корнем для.

Доказательство. Пусть. В этом случае,. В выражении дляпервое слагаемое не делится на, следовательно, линейный двучленне является делителем, т. е.сне является корнем для. Если же, то. Первое слагаемое в этой сумме делится на, а второе – на, следовательно, с − (к−1)-кратный корень для. Теорема доказана.

Следствие.Если числосявляется корнем для,,…,, но не является корнем для, то в этом случаес −к-кратный корень многочлена.

П р и м е р.Чему равен показатель кратности корня 2 для многочлена?

Решение.Приимеем. Найдем:;. Найдем:;. Производная 3-го порядка:;, таким образом, кратность корня 2 для многочленаравна 3.

2.4. Наибольший общий делитель двух многочленов. Алгоритм Евклида

Определение. Наибольшим общим делителем (НОД) двух отличных от нуля многочленов иназывается многочленнаибольшей степени среди многочленов, делящих оба многочленаи.

Обозначается наибольший общий делитель многочленов исимволом. Другими словами, наибольшим общим делителем двух отличных от нуля многочленовиназывается такой многочлен, который является их общим делителем и вместе с тем сам делится на любой другой общий делитель этих многочленов.

Находить наибольший общий делитель двух многочленов можно с помощью алгоритма Евклида, который состоит в следующем. Выполним цепочку делений с остатком: ,;,;,; …;,,.

Процесс конечен, т. е. на некотором шагу деление выполнится без остатка, потому что степень каждого последующего остатка меньше степени предыдущего. Остаток и будет наибольшим общим делителем для многочленов.

Наибольший общий делитель двух многочленов определяется с точностью до постоянного множителя. Поэтому, чтобы избежать дробных коэффициентов, можно умножать или сокращать делитель на любое не равное нулю число, причем не только начиная какое-либо из последовательных делений, но и в процессе этого деления.

Это приведет к искажению частного, но интересующие нас остатки будут приобретать лишь множители нулевой степени, что допускается при отыскании НОД.

П р и м е р. Найти наибольший общий делитель для многочленов ив кольце вещественных чисел.

Решение. Обозначим ,. Найдем остаток:

x5 - 2x4 – 7x3 + 7x2 +5x – 4 x5 + 2x4 – 3x3						x2 +2x – 3
						x3 – 4x2 +4x − 13
− 4x4 – 4x3 +7x2 − 4x4 – 8x3 +12x2
	4x3 – 5x2 +5x
	4x3 + 8x2 – 12x
		− 13x2 + 17x − 4 − 13x2 – 26x + 39
		43x − 43

С точностью до постоянного множителя остаток равен. Найдем остаток. Для этого многочленразделим на:

x2 + 2x − 3 x2 −x				x − 1
				x + 3
	3x – 3 3x – 3
		0

Получили, что , следовательно, для многочленовинаибольшим общим делителем является, т. е..

Наибольший общий делитель допускает линейное представление в виде, гдеи− некоторые многочлены. Можно считать при этом, что если степени многочленовибольше нуля, то степеньменьше степени, а степеньменьше степени. По алгоритму Евклида:,,, …,,. Получили, что. Возвращаясь назад, придем к доказываемому равенству.

П р и м е р.Для многочленовинайти такие многочленыи, чтобы.

Решение.В предыдущем примере нашли, что. Используя обратный ход в алгоритме Евклида, получим . После раскрытия скобок получим,.

П р и м е р.Найти многочленыи, чтобы выполнялось равенстводля многочленови.

Решение.Найдемтакое, что:

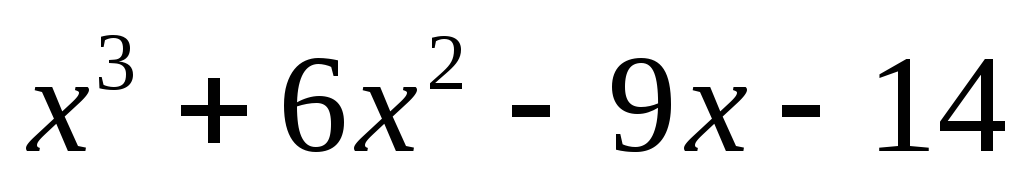
	1

Получили ,,. Далее.

То есть . С другой стороны,. Далее.

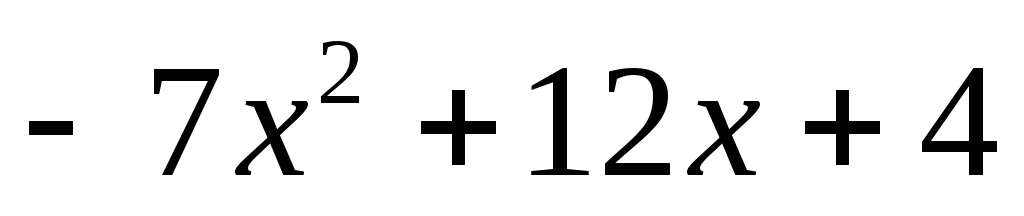
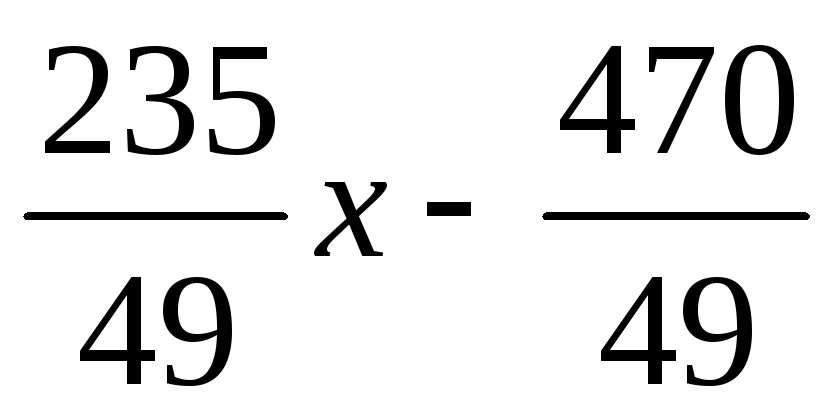
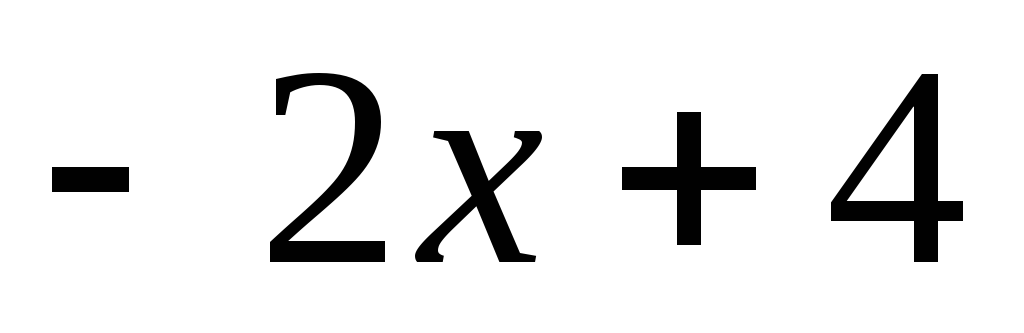
		0

Получили, что , т. е.. Учитывая, что, получим, т. е.,.