
- •Вещественные и комплексные числа
- •1.1. Множества. Обозначения. Логические символы
- •1.2. Вещественные числа и их основные свойства
- •Основные свойства вещественных чисел
- •1.3. Абсолютная величина числа
- •1.4. Геометрическое изображение вещественных чисел
- •1.5. Наиболее употребляемые числовые множества
- •1.6. Прямоугольная система координат на плоскости Две взаимно перпендикулярные оси Ох иОу, имеющие общее началоОи одинаковую масштабную единицу, образуютпрямоугольную систему координат на плоскости.
- •1.7. Полярная система координат
- •1.8. Комплексные числа. Алгебраическая форма комплексного
- •1.9. Тригонометрическая форма комплексного числа
- •1.10. Возведение комплексного числа в степень с целым показателем. Формула Муавра
- •1.11. Извлечение корня из комплексного числа
- •1.12. Извлечение квадратного корня из комплексного числа
- •1.13. Показательная форма комплексного числа
- •Многочлены
- •Над многочленами. Корни многочленов. Теорема Безу
- •2.2. Схема Горнера
- •2.3. Кратные корни
- •2.4. Наибольший общий делитель двух многочленов. Алгоритм Евклида
- •Свойства делимости многочленов
- •2.5. Взаимно простые многочлены
- •Свойства взаимно простых многочленов
- •2.6. Корни квадратного уравнения
- •2.7. Корни кубического уравнения
- •2.8. Корни уравнения четвертой степени
- •Индивидуальные задания по теме
Свойства делимости многочленов
1. Если
![]() делится на
делится на![]() ,
а
,
а![]() делится на
делится на![]() ,
то
,
то![]() делится на
делится на![]() .
.
Доказательство.
Так как
![]() делится на
делится на![]() ,
а
,
а![]() делится на
делится на![]() ,
то существуют многочлены
,
то существуют многочлены![]() и
и![]() такие, что
такие, что![]() и
и![]() .
Поэтому
.
Поэтому![]() ,
т. е.
,
т. е.![]() делится на
делится на![]() .
.
Если
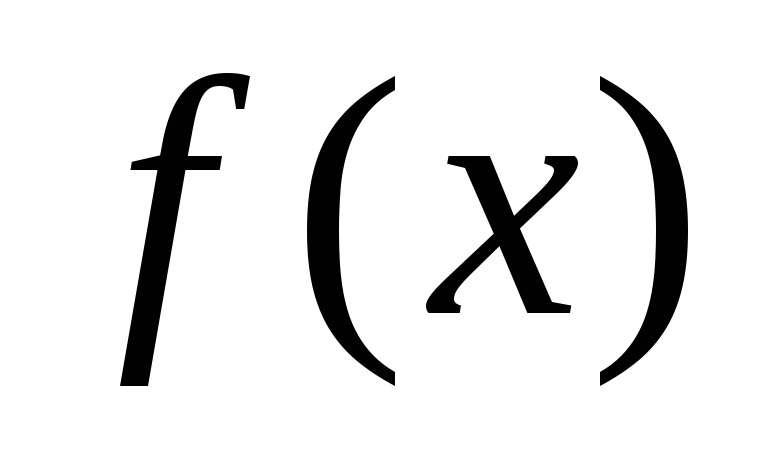 и
и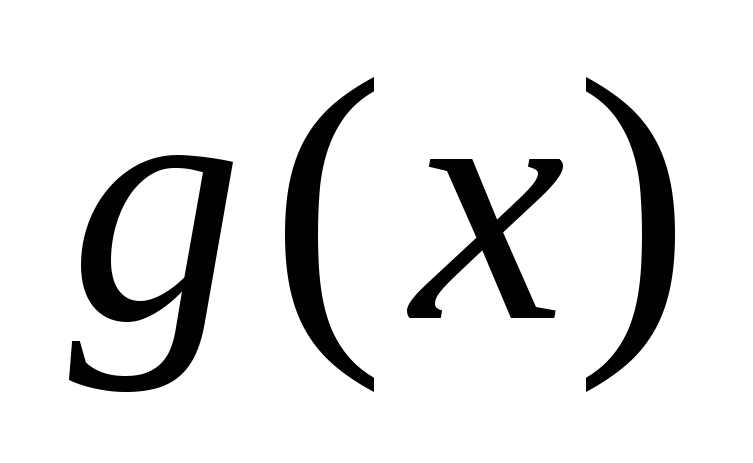 делятся на
делятся на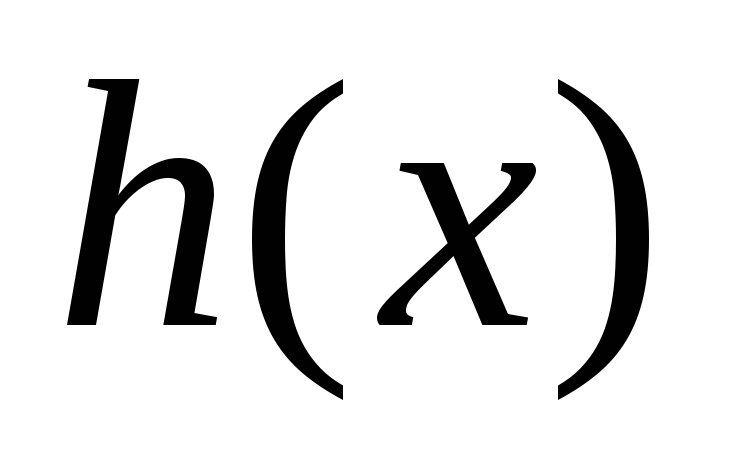 ,
то
,
то делится на
делится на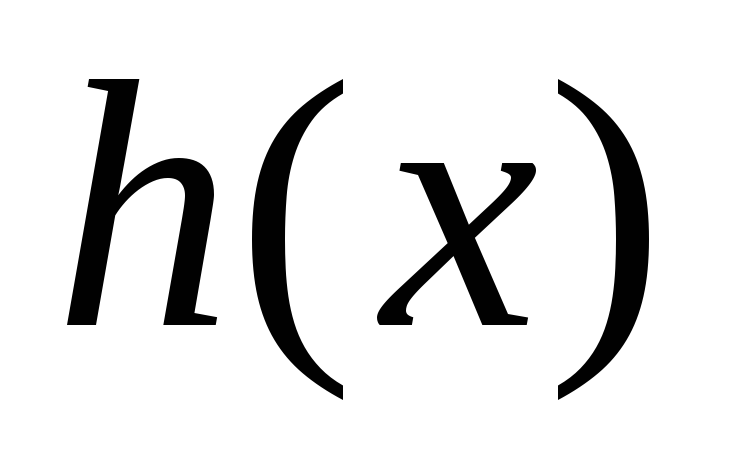 .Доказать
аналогично доказательству свойства
1.
.Доказать
аналогично доказательству свойства
1.Если
 делится на
делится на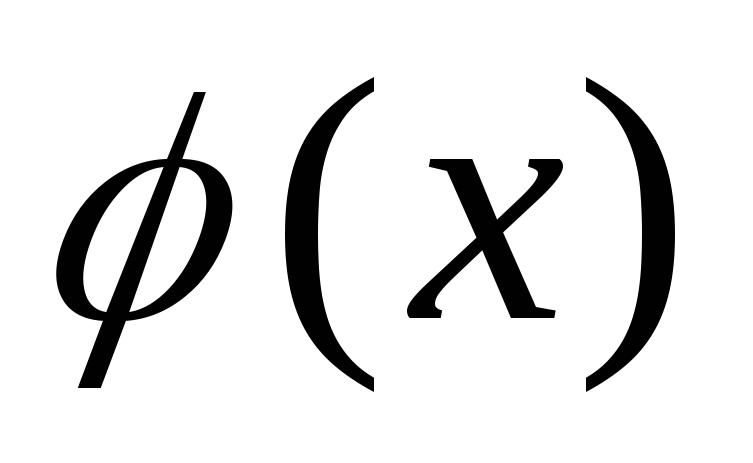 ,
то
,
то произведение
произведение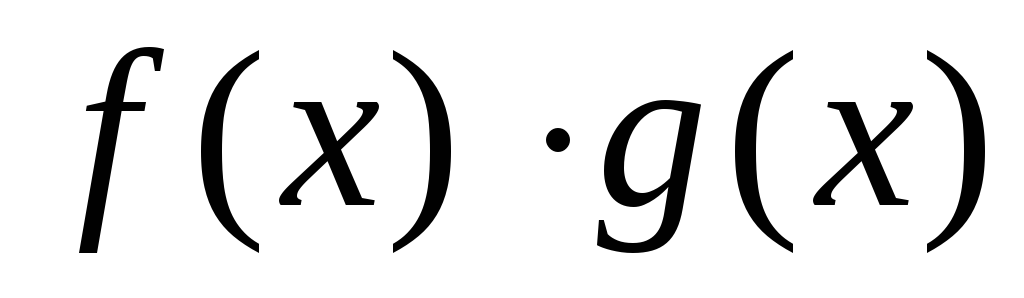 делится на
делится на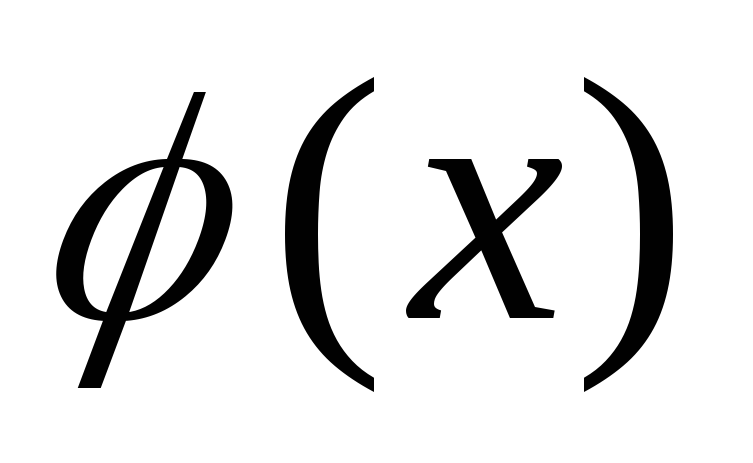 .Это свойство
предлагается доказать самостоятельно.
.Это свойство
предлагается доказать самостоятельно.Если
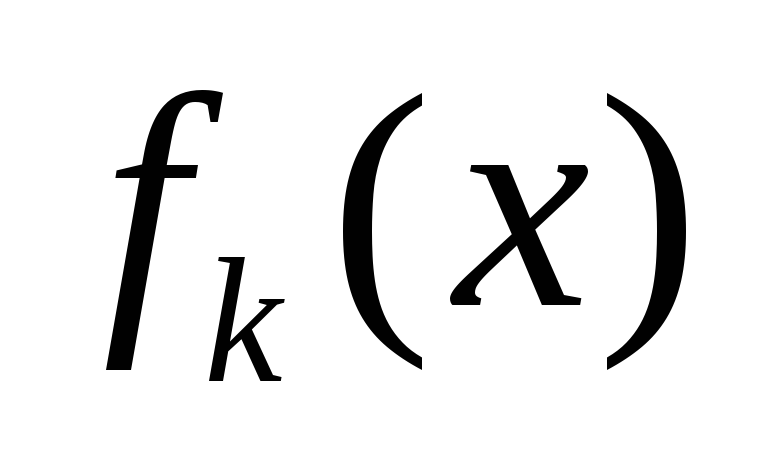 ,
,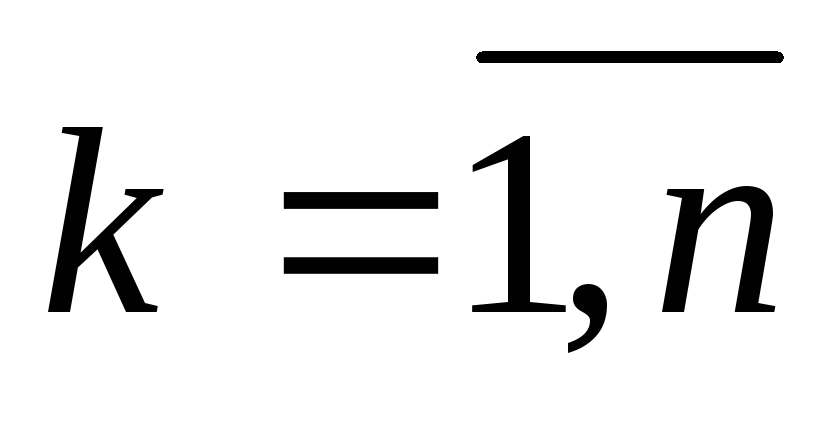 делится на
делится на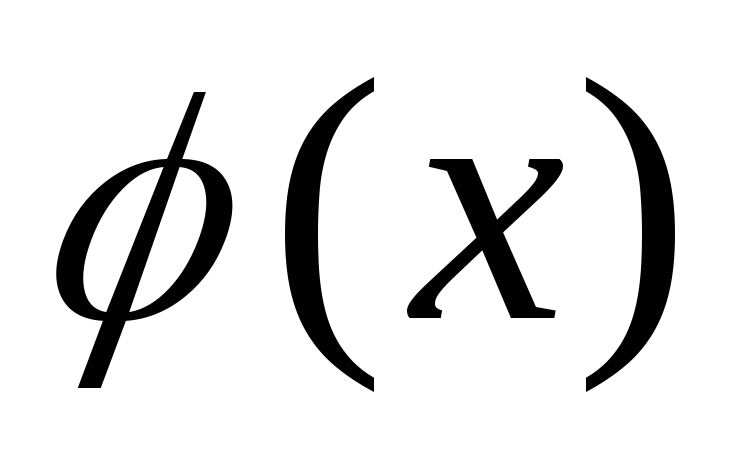 ,
то
,
то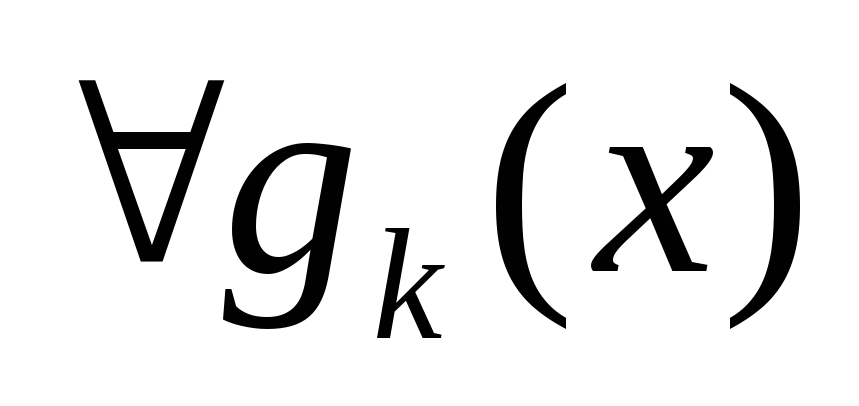 ,
, сумма
сумма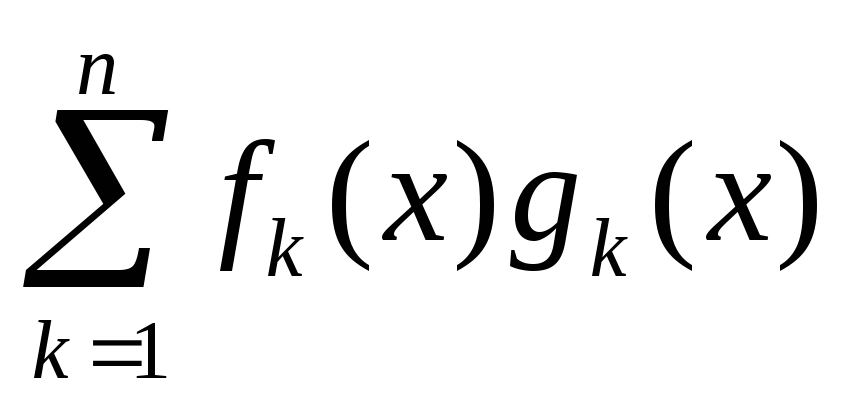 делится на
делится на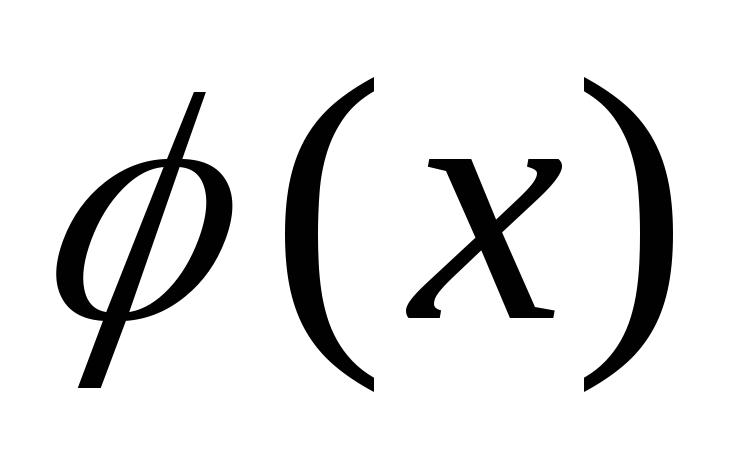 .Это свойство
предлагается доказать самостоятельно.
.Это свойство
предлагается доказать самостоятельно.Любой многочлен
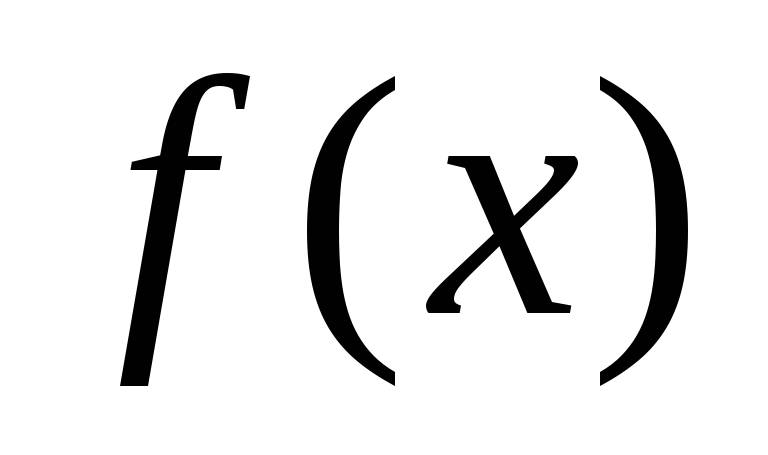 делится на многочлен нулевой степени.
делится на многочлен нулевой степени.
Доказательство.
Пусть С, С
0
– многочлен
нулевой степени. Тогда
![]() ,
т. е.
,
т. е.![]() делится наС.
делится наС.
Если
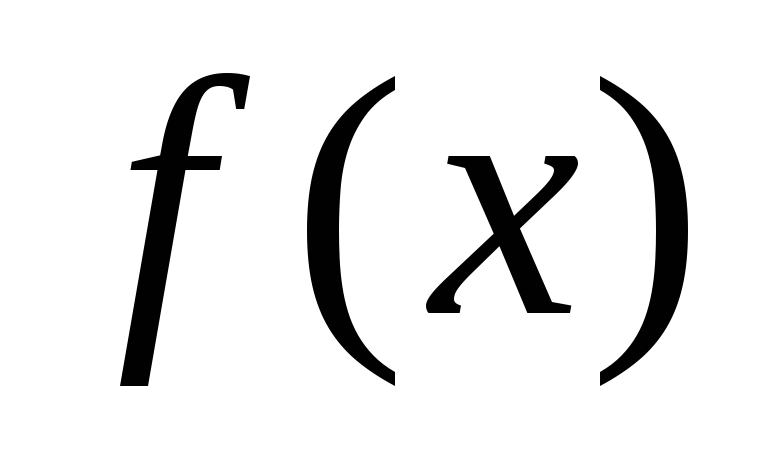 делится на
делится на ,
то
,
то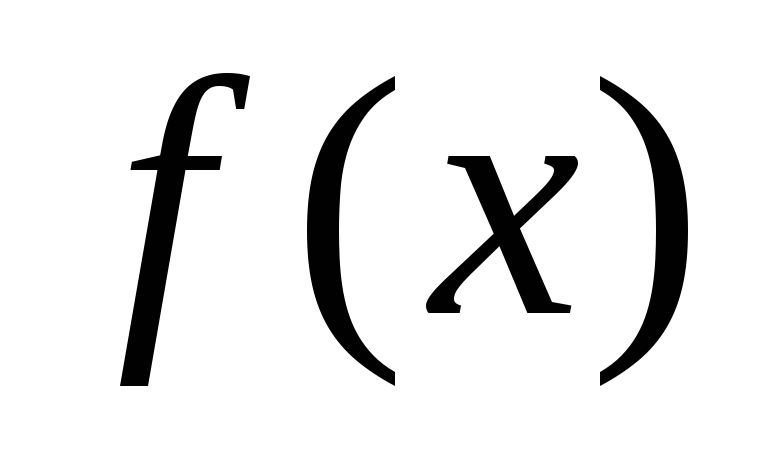 делится на
делится на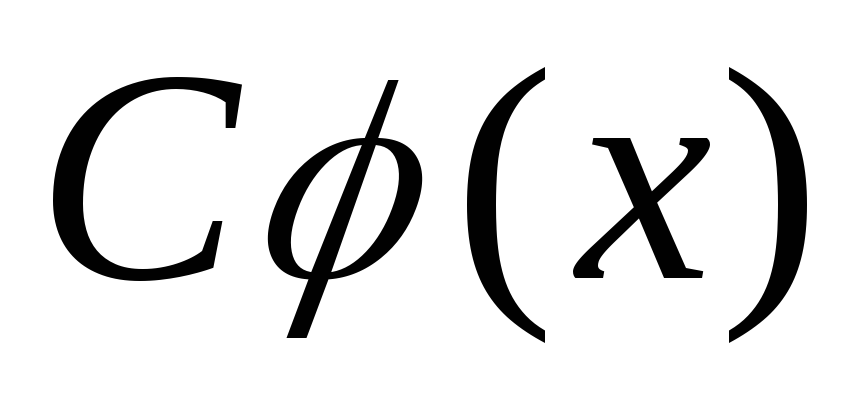 ,
где
,
где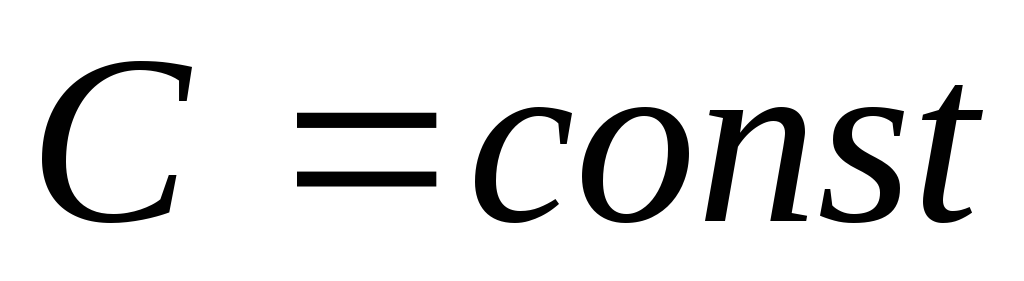 .Это свойство
предлагается доказать самостоятельно.
.Это свойство
предлагается доказать самостоятельно.Если
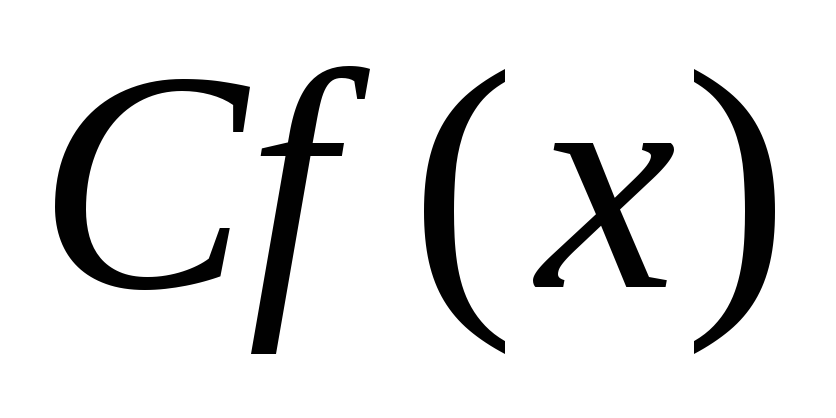 ,
,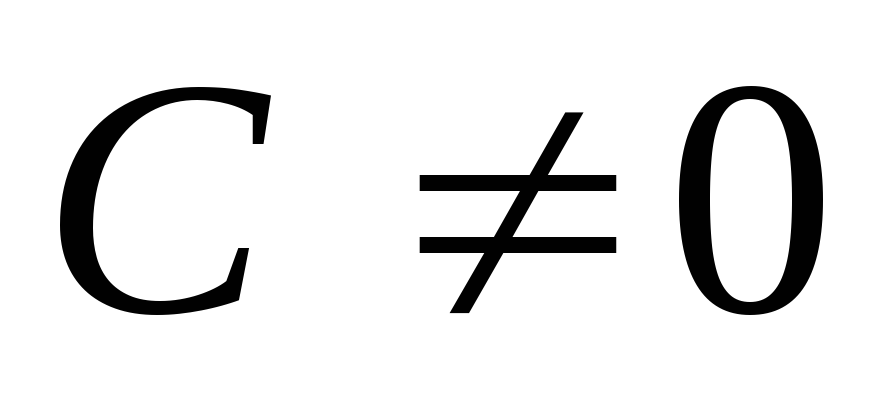 − делители многочлена
− делители многочлена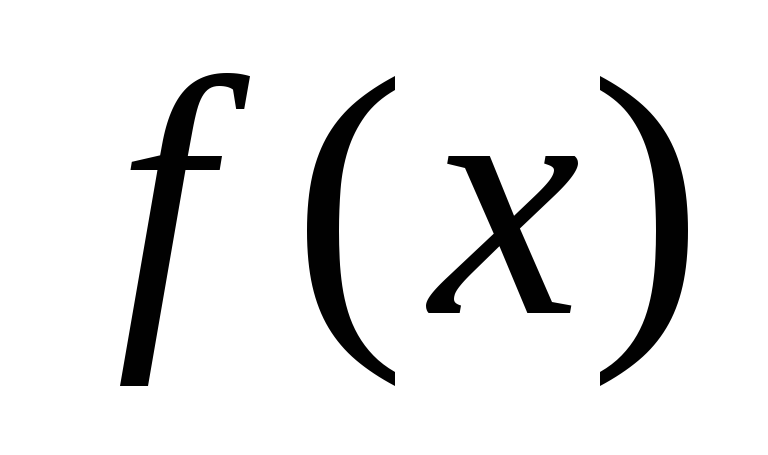 ,
то они имеют такую же степень, что и
,
то они имеют такую же степень, что и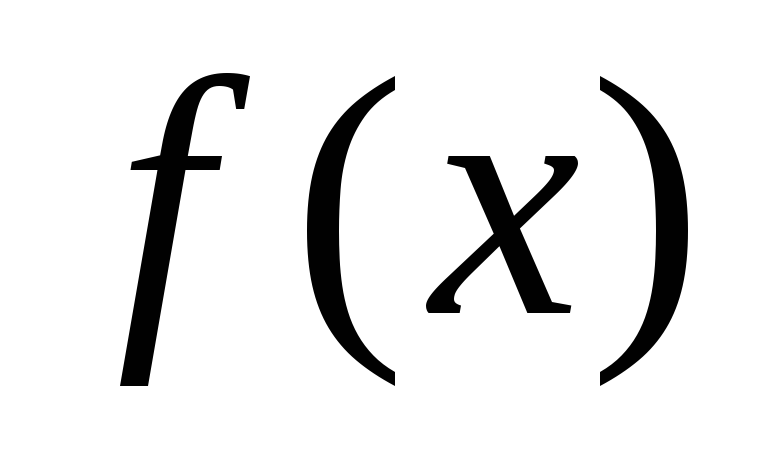 .
.
Доказательство.
Многочлен
![]() можно представить в виде
можно представить в виде![]() .
Из того, что
.
Из того, что![]() ,
следует доказываемое утверждение.
,
следует доказываемое утверждение.
Многочлены
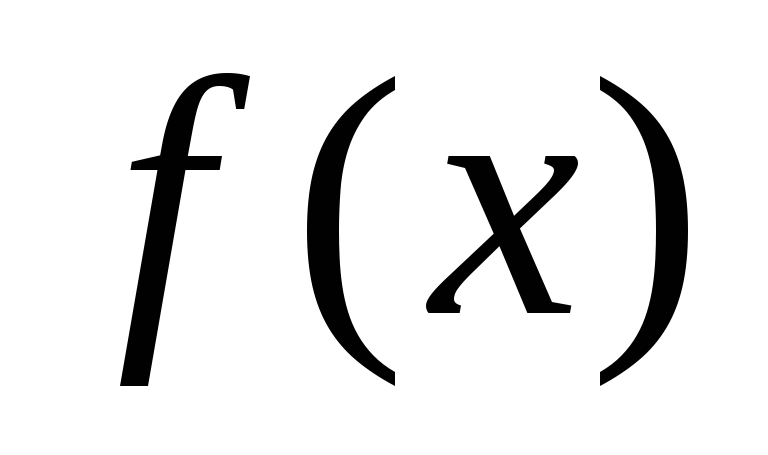 и
и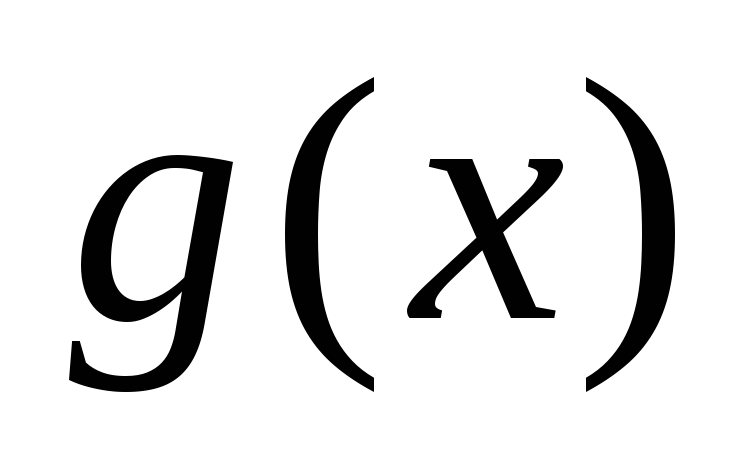 делятся друг на друга, если существует
делятся друг на друга, если существует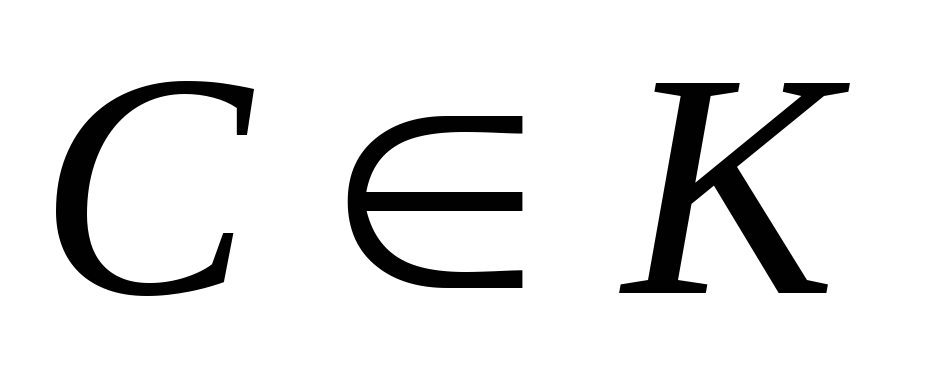 ,
,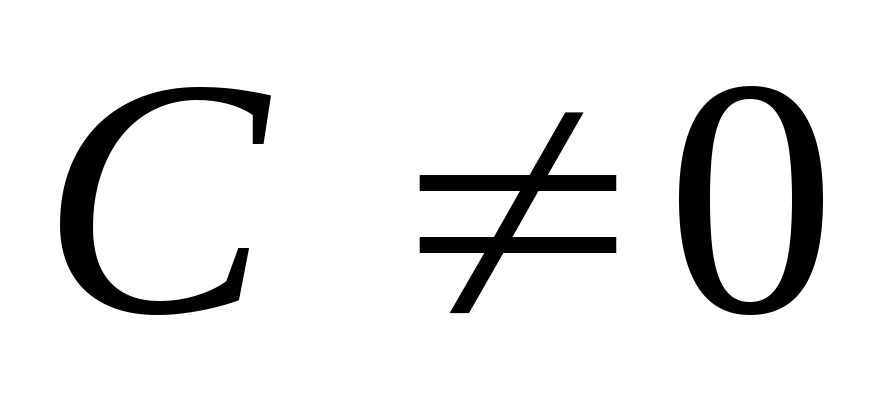 такое, что
такое, что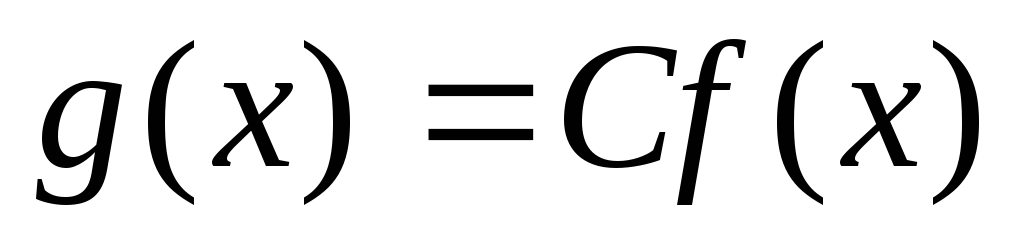 .Это свойство
предлагается доказать самостоятельно.
.Это свойство
предлагается доказать самостоятельно.Если
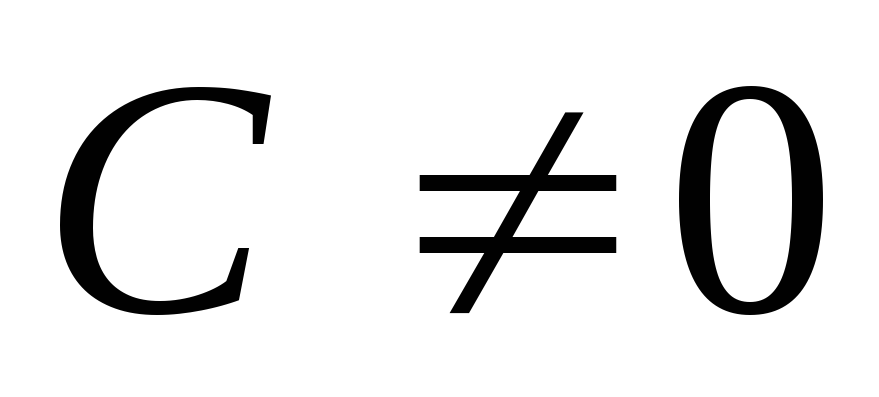 ,
то делитель одного из многочленов
,
то делитель одного из многочленов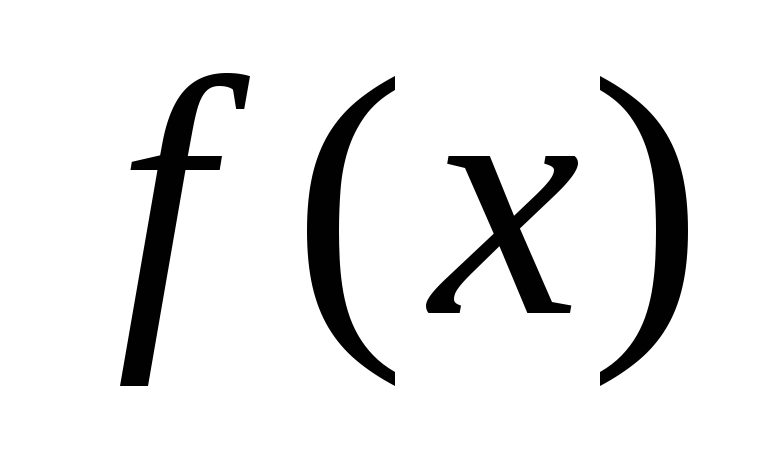 и
и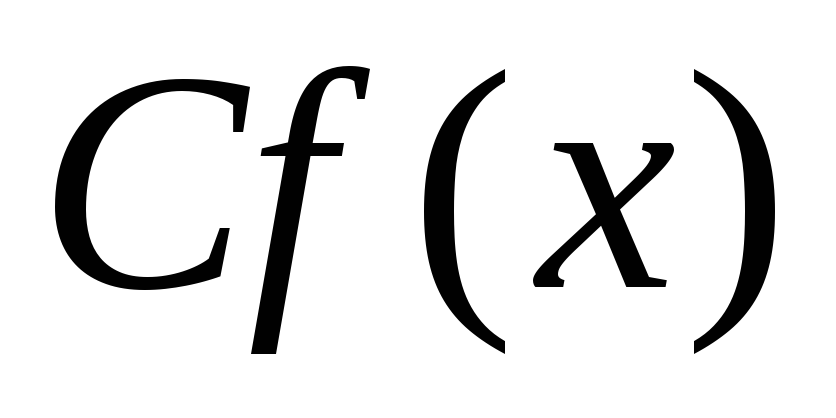 будет делителем и другого многочлена.
будет делителем и другого многочлена.
Доказательство.
Пусть многочлен
![]() является делителем
является делителем![]() .
Тогда существует многочлен
.
Тогда существует многочлен![]() такой, что
такой, что![]() .
Поэтому
.
Поэтому![]() ,
т. е.
,
т. е.![]() является делителем
является делителем![]() .
Если же
.
Если же![]() является делителем
является делителем![]() ,
то существует многочлен
,
то существует многочлен![]() такой, что
такой, что![]() и
и![]() ,
т. е.
,
т. е.![]() является делителем
является делителем![]() .
.
2.5. Взаимно простые многочлены
Определение.Два многочлена называютсявзаимно простыми, если их нормализованный наибольший общий делитель равен 1, т. е. эти многочлены не имеют никаких общих делителей, кроме констант.
Теорема.Для того чтобы многочлены![]() и
и![]() были взаимно просты, необходимо и
достаточно, чтобы существовали многочлены
были взаимно просты, необходимо и
достаточно, чтобы существовали многочлены![]() и
и![]() такие, что
такие, что![]() .
.
Доказательство.Если![]() ,
то всякий общий делитель для
,
то всякий общий делитель для![]() и
и![]() делит единицу и является константой.
Если же
делит единицу и является константой.
Если же![]() и
и![]() взаимно простые, то их нормализованный
наибольший общий делитель 1 имеет
линейное представление
взаимно простые, то их нормализованный
наибольший общий делитель 1 имеет
линейное представление![]() .
.
Свойства взаимно простых многочленов
Если произведение
 делится на
делится на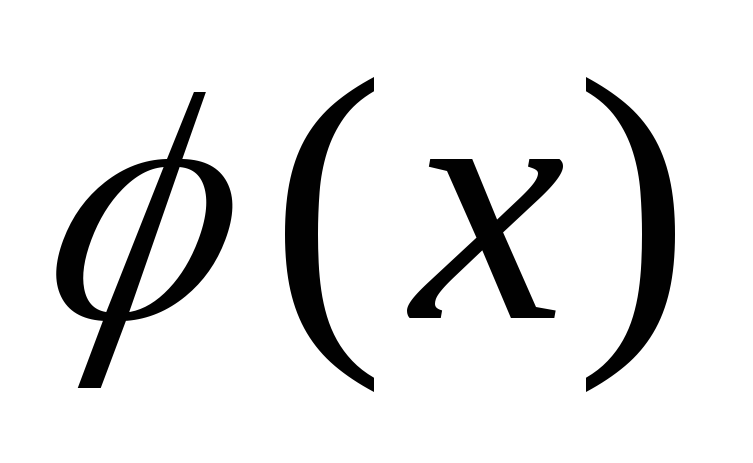 и
и ,
то
,
то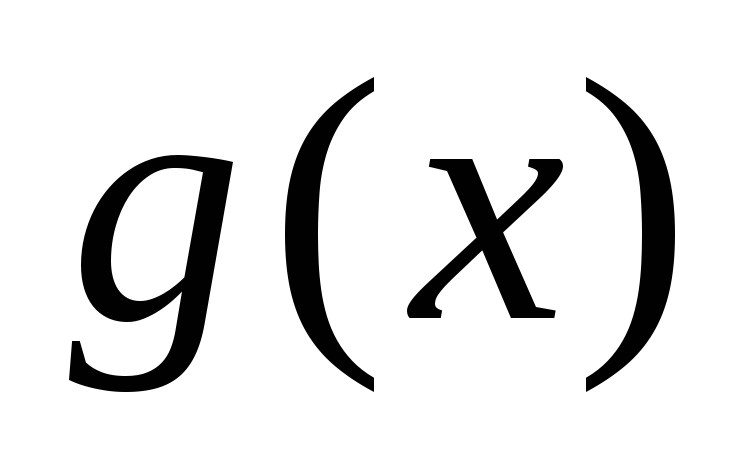 делится
на
делится
на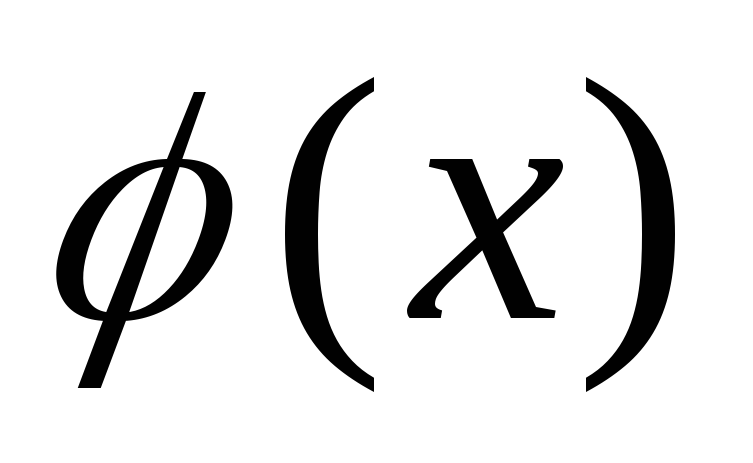 .
.
Доказательство.Так как![]() ,
то найдутся многочлены
,
то найдутся многочлены![]() и
и![]() такие, что
такие, что![]() .
Умножим это равенство на
.
Умножим это равенство на![]() ,
получим, что
,
получим, что![]() .
Оба слагаемых в правой части делятся
на
.
Оба слагаемых в правой части делятся
на![]() (первое потому, что по условию
(первое потому, что по условию![]() делится на
делится на![]() ).
Следовательно,
).
Следовательно,![]() делится
на
делится
на![]() .
.
Если
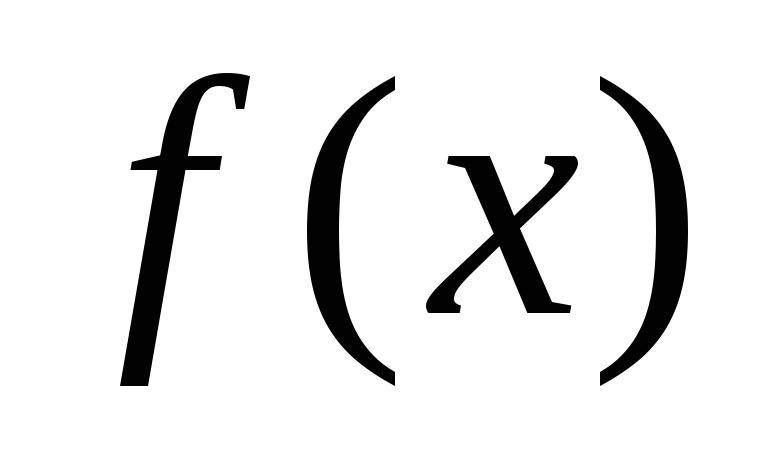 и
и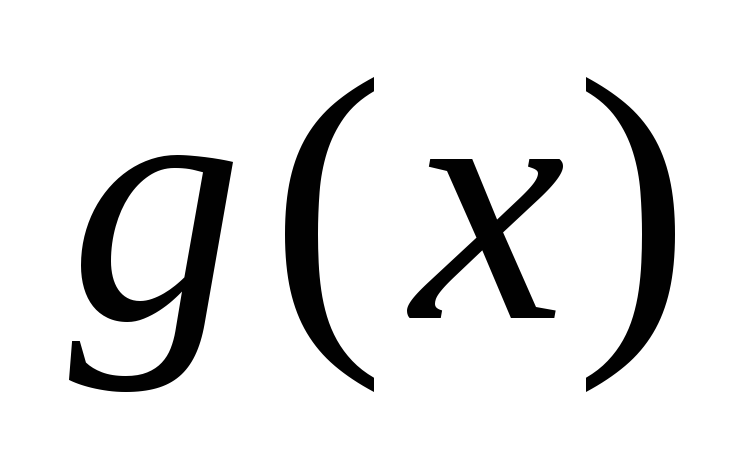 взаимно просты с
взаимно просты с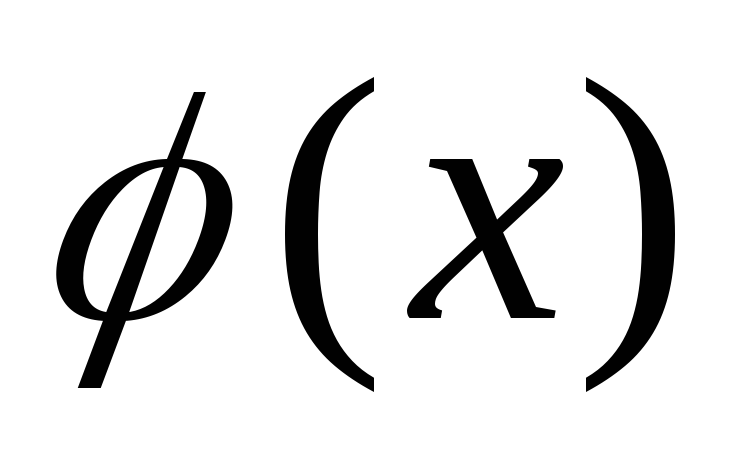 ,
то произведение
,
то произведение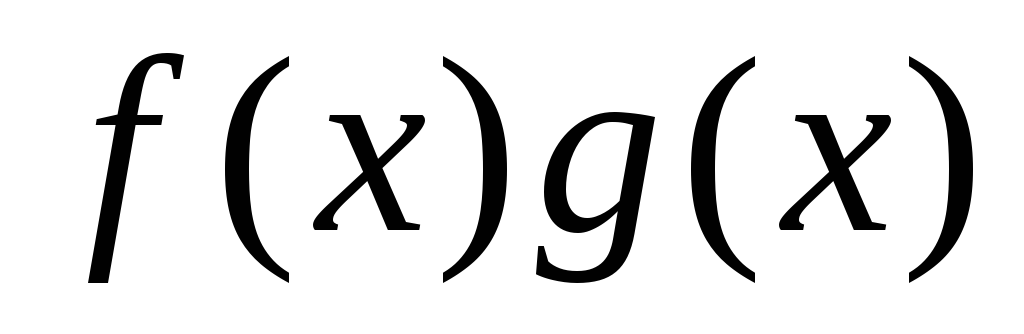 взаимно просто с
взаимно просто с .
.
Доказательство.Многочлены![]() и
и![]() взаимно просты с
взаимно просты с![]() ,
следовательно, существуют многочлены
,
следовательно, существуют многочлены![]() и
и![]() такие, что
такие, что![]() .
Умножим обе части равенства на
.
Умножим обе части равенства на![]() .
Получим
.
Получим![]() .
Делитель
.
Делитель![]() и
и![]() является также делителем
является также делителем![]() .
Однако
.
Однако![]() и
и![]() взаимно простые, следовательно,
произведение
взаимно простые, следовательно,
произведение![]() взаимно просто с
взаимно просто с![]() .
.
Если многочлены
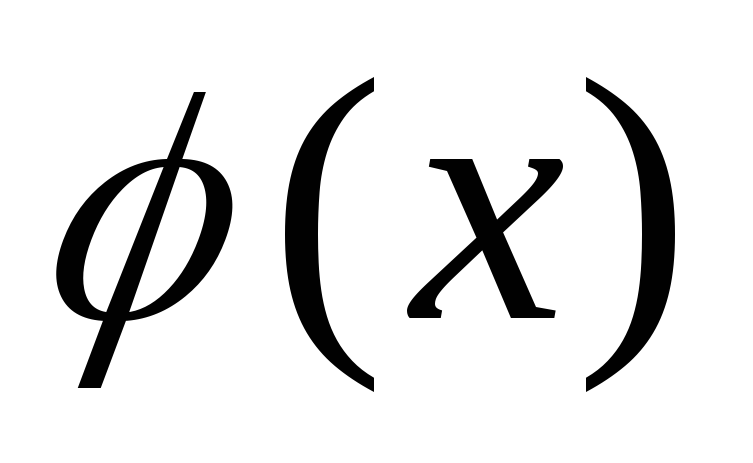 и
и взаимно просты, многочлен
взаимно просты, многочлен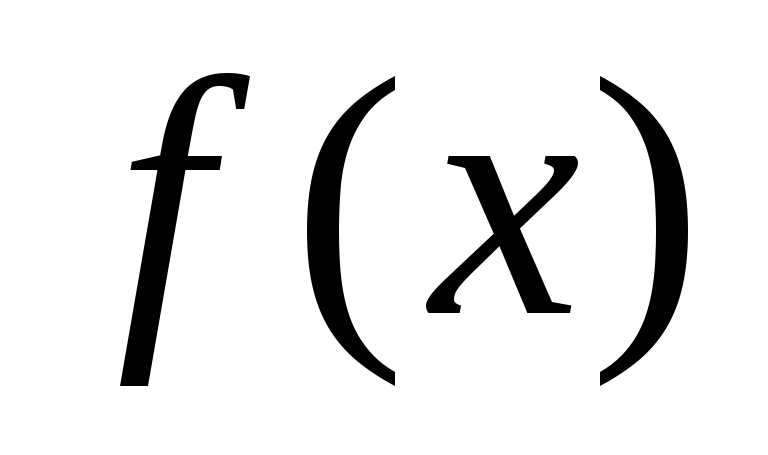 делится на каждый из них, то
делится на каждый из них, то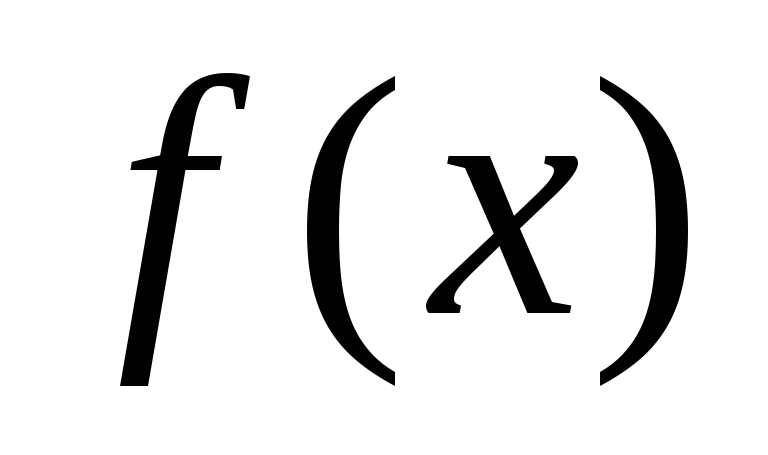 делится на произведение
делится на произведение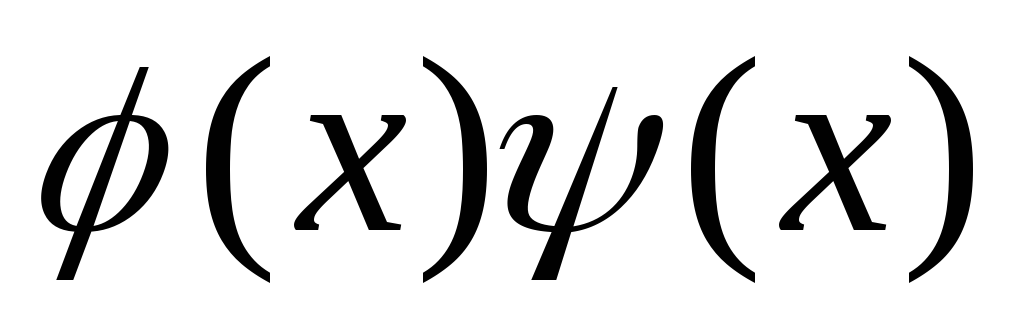 .
.
Доказательство.Многочлен![]() делится на
делится на![]() ,
поэтому существует многочлен
,
поэтому существует многочлен![]() такой, что
такой, что![]() .
многочлен
.
многочлен![]() делится на
делится на![]() ,
следовательно, произведение
,
следовательно, произведение![]() делится на
делится на![]() .
Многочлены
.
Многочлены![]() и
и![]() взаимно просты, поэтому
взаимно просты, поэтому![]() делится на
делится на![]() ,
т. е. существует многочлен
,
т. е. существует многочлен![]() такой, что
такой, что![]() и
и![]() ,
ч. и т. д.
,
ч. и т. д.
Определение.НОД многочленов![]() ,
,![]() ,…,
,…,![]() ,
,![]() равен наибольшему общему делителю
многочлена
равен наибольшему общему делителю
многочлена![]() и многочленов
и многочленов![]() ,…,
,…,![]() .
.
Определение.Система многочленов![]() называется взаимно простой, если
наибольшими общими делителями этих
многочленов являются лишь многочлены
нулевой степени.
называется взаимно простой, если
наибольшими общими делителями этих
многочленов являются лишь многочлены
нулевой степени.
Замечание.Если![]() ,
то многочлены попарно могут не быть
взаимно простыми:
,
то многочлены попарно могут не быть
взаимно простыми:![]() ,
,![]() ,
,![]()
