1.12. Извлечение квадратного корня из комплексного числа

Извлечение корня из комплексного числа можно осуществить, не обращаясь к тригонометрической форме. Выведем алгебраическую формулу для выполнения этого действия.

Пусть . Интересен случай, поэтому рассмотрим только его. Тогда. Это равносильно системе уравнений:

(1.12)

Эта задача имеет вещественные решения, так как всегда существует квадратный корень из комплексного числа. Из второго уравнения системы , подставляя которое в первое уравнение системы (1.12), получаем биквадратное уравнение относительно неизвестного. Его решениями являются, поэтому. Для любого вещественного числаtсуществует функция, которая задается следующим образом:

(1.13)

С учетом введенной функции получаем формулу для нахождения квадратного корня из комплексного числа:

. (1.14)

П р и м е р. Найти корни уравнения.

Решение.Корни уравненияравны. Пусть=. Относительно неизвестныхиимеем систему уравнений

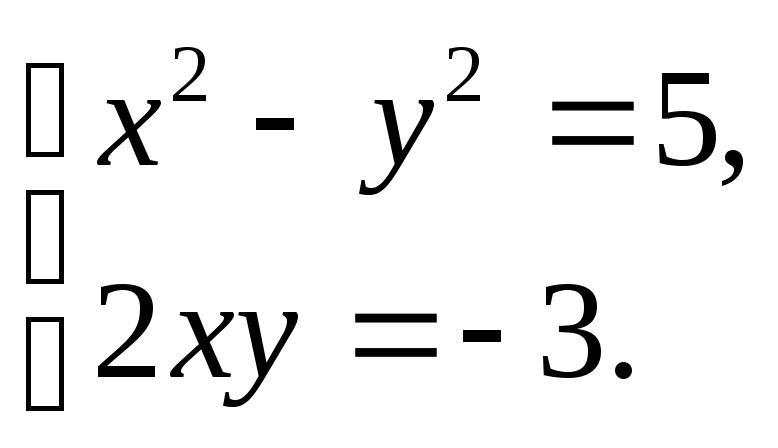
Из второго уравнения этой системы , поэтому относительно неизвестногополучаем уравнение, или. Учитывая, чтовещественное число, находим, т. е.. Следовательно,. Таким образом,.

1.13. Показательная форма комплексного числа

В различных разделах современной математики, а также ее приложениях применяется показательная форма комплексного числа. В основе показательной формы лежит формула Эйлера, устанавливающая связь между тригонометрическими функциями действительного аргумента и показательной функцией мнимого аргумента.

Первая формула Эйлера (без вывода):

, (1.15) где е – иррациональное число, принятое за основание натуральных логарифмов (е 2,718).

Если в формуле произвести замену по формуле (1.15), то получим. Это и есть показательная форма комплексного числа. В этой записи− модуль комплексного числа,− его аргумент. Заменим в формуле (1.15)на -, получим вторую формулу Эйлера:

. (1.16)

Из формул (1.15) и (1.16) следует, что

, . (1.17)

Равенства (1.17) также называются формулами Эйлера и выражают тригонометрические функции действительного переменного через показательные функции мнимого аргумента. Формулы (1.17) справедливы и тогда, когдазаменяется любым комплексным числом, т. е.,. Эти равенства принимают за определение косинуса и синуса комплексного аргумента.

Тригонометрические функции комплексного переменного также периодичны, причем период . Покажем это для функции. Действительно,====, так как по формулам Эйлера,. Примечательно, что все формулы обычной тригонометрии сохраняют свою силу в комплексной плоскости, например,. Однако в отличие от действительных чисел могут иметь место неравенстваи. Например,

.

2. Многочлены

0. Многочлен от одной переменной. Действия

Над многочленами. Корни многочленов. Теорема Безу

Определение.Одночленом от переменнойс коэффициентом из множестваАназывается выражение вида, где,− целое неотрицательное число.

Считается, что , поэтому все элементы множестваАявляются одночленами частного вида.

Определение.Одночлены называются подобными, если показатели степениодинаковы.

Подобные одночлены складываются по правилу , которое называетсяправилом приведения подобных членов. Для одночленов определяется и действие умножения.

Определение.Многочленомn-й степени от неизвестногохназывается сумма целых неотрицательных степеней, не превышающихп, неизвестногох, взятых с некоторыми числовыми коэффициентами, т. е. выражение вида

, (2.1)

причем .

В многочлене порядок слагаемых безразличен, и подобные одночлены можно соединять по правилу приведения подобных членов. Запись (2.1) называется канонической формоймногочлена. Иногда удобно записывать многочлены в порядке возрастания показателей. Многочлены обозначаются,,и т. д.

Пусть , причем. Одночленназываетсявысшим (старшим) членоммногочлена, а показатель−степеньюмногочленаи обозначается. Нулевой многочлен не имеет высшего члена в смысле данного определения и считается, что он равен 0. Степень нулевого многочлена считается равной символу.

Определение.Два многочлена называются равными (или тождественно равными), если они составлены в канонической записи из одинаковых одночленов, т.е.в том и только в том случае, если,.

Иными словами, в равных многочленах равны коэффициенты при одинаковых степенях неизвестного х.

Определение.Суммойдвух многочленов называется многочлен, получающийся при объединении одночленов, составляющих слагаемые. После объединения необходимо привести подобные члены. Таким образом,=++ … + +.

Определение.Произведениемдвух многочленов называется многочлен, составленный из произведений всех членов первого сомножителя на все члены второго. После приведения подобных членов получим, что=.

Коэффициент при равен, если считать, чтоприипри.

Пусть даны два многочлена и, причеми. Тогда произведениесодержит ненулевой одночлен, который будет высшим для произведения данных многочленов, так как остальные произведения членовна членыимеют меньшую, чемстепень.

Для любых двух многочленов иможно найти такие многочленыи, что

, (2.2)

причем степень меньше степениили же. Многочленыи, удовлетворяющие условию (2.2), определяются однозначно. Многочленназываетсячастным, а−остатком.

Определение. Пусть даны два ненулевых многочленаи. Если остаток от делениянаравен нулю, то многочленназываетсяделителеммногочлена.

Определение.Если− многочлен,, тоназывается значением многочленапри.

Теорема.Остаток от деления многочленана линейный многочленравен значениюмногочленапри.

Доказательство.Согласно (2), где− многочлен нулевой степени, т. е. константа. Переходя в этом равенстве к значениям при, получим, откуда. Теорема доказана.

П р и м е р. Найти остаток от деления многочленана многочлен.

Решение. По доказанной ранее теореме.

Если для полиномов исуществует такой полином, что, то говорят, что полиномделится на полином. Рассмотрим вопрос о делимостина линейный двучлен, где.

Теорема (Безу).Для того чтобы полиномделился на, необходимо и достаточно, чтобы.

Доказательство.А.Необходимость.Пустьделится на, т. е.. Тогда. Б.Достаточность. Пусть. Тогда в равенствебудет, т. е.. Теорема доказана.

Определение.Числосназываетсякорнем полинома, если.

С использованием этого определения теорема Безу может быть сформулирована следующим образом: для того чтобы полином делился на двучлен, необходимо и достаточно, чтобыс было корнем. Таким образом, отыскание корней многочлена равносильно отысканию его линейных делителей.

П р и м е р.Является ли линейный многочленделителем многочлена?

Решение.Найдем:, следовательно,не является делителем многочлена.